Docs
AI
DL
RNN
LSTM

Long Short-Term Memory (LSTM)

For detailed explanation and summary see:

Motivation

截屏2020-08-21 12.10.50

  • Memory cell
  • Inputs are “commited” into memory. Later inputs “erase” early inputs
  • An additional memory “cell” for long term memory
  • Also being read and write from the current step, but less affected like 𝐻

LSTM Operations

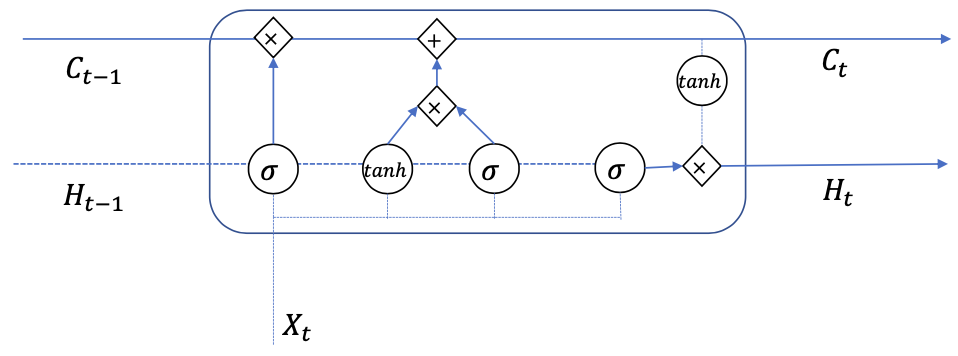
截屏2020-08-21 12.16.54
  • Forget gate
  • Input Gate
  • Candidate Content
  • Output Gate

Forget

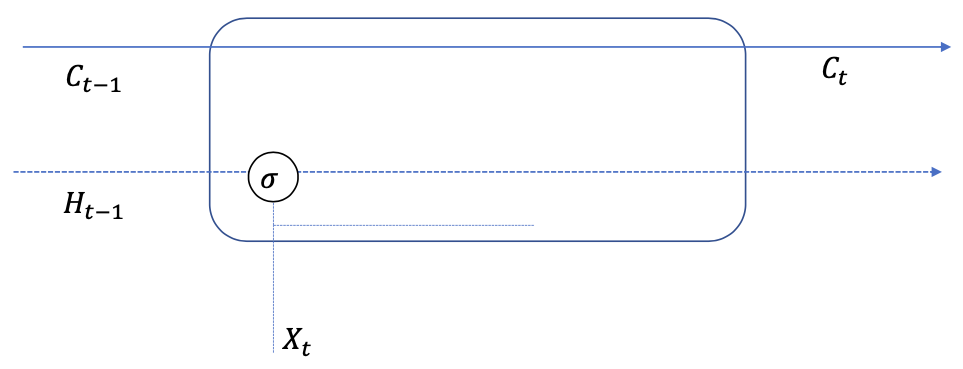
截屏2020-08-21 12.15.49

  • Forget: remove information from cell $C$

  • What to forget depends on:

    • the current input $X\_t$
    • the previous memory $H\_{t-1}$

  • Forget gate: controls what should be forgotten

    $$ F\_{t}=\operatorname{sigmoid}\left(W^{F X} X\_{t}+W^{F H} H\_{t-1}+b^{F}\right) $$

  • Content to forget:

    $$ C = F\_t * C\_{t-1} $$
    • $F\_{t,j}$ near 0: Forgetting the content stored in $C\_j$

Write

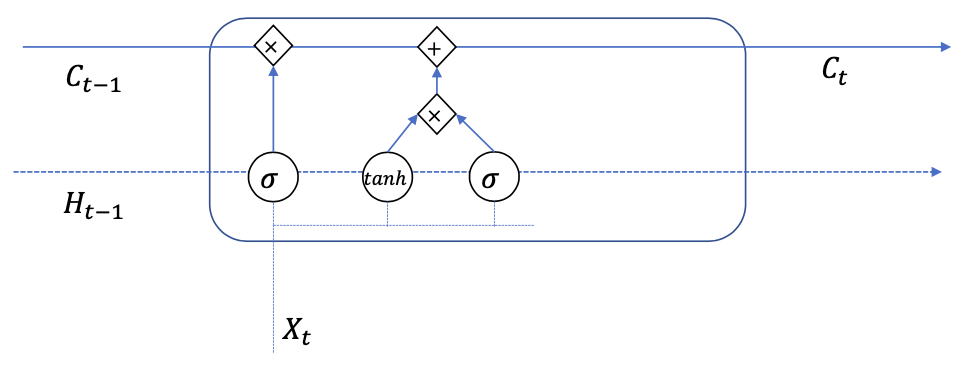
截屏2020-08-21 12.15.52

  • Write: Adding new information for cell $C$

  • What to forget depends on:

    • the current input $X\_t$
    • the previous memory $H\_{t-1}$

  • Input gate: controls what should be add

    $$ I\_{t}=\operatorname{sigmoid}\left(W^{I X} X\_{t}+W^{I H} H\_{t-1}+b^{I}\right) $$

  • Content to write:

    $$ \tilde{C}\_{t}=\tanh \left(W^{C X} X\_{t}+W^{C H} H\_{t-1}+b^{I}\right) $$

  • Write content:

    $$ C=C\_{t-1}+I\_{t} * \tilde{C}\_{t} $$

Output

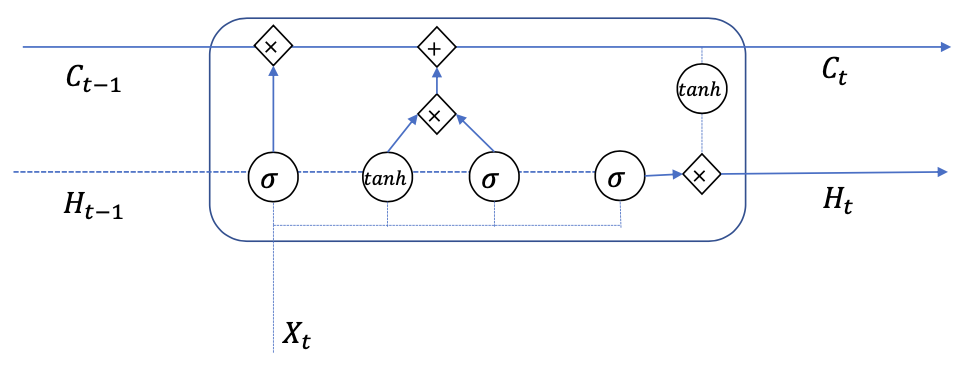
截屏2020-08-21 12.15.54

  • Output: Reading information from cell 𝐶 (to store in the current state $H$)

  • How much to write depends on:

    • the current input $X\_t$
    • the previous memory $H\_{t-1}$

  • Forget gate: controls what should be output

    $$ O\_{t}=\operatorname{sigmoid}\left(W^{OX} X\_{t}+W^{OH} H\_{t-1}+b^{O}\right) $$

  • New state

    $$ H\_t = O\_t * \operatorname{tanh}(C\_t) $$

LSTM Gradients

截屏2020-08-21 12.16.32

Truncated Backpropagation

What happens if the sequence is really long (E.g. Character sequences, DNA sequences, video frame sequences …)? $\to$ Back-propagation through time becomes exorbitant at large $T$

Solution: Truncated Backpropagation

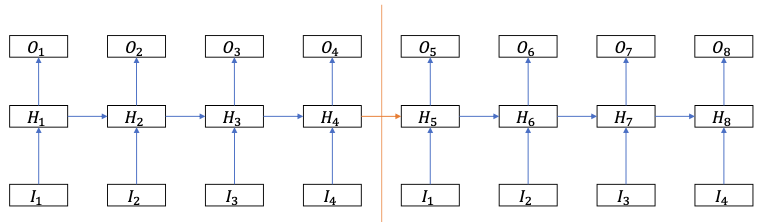
截屏2020-08-21 12.49.17
  • Divide the sequences into segments and truncate between segments
  • However the memory is kept to remain some information about the past (rather than resetting)

TDNN vs. LSTM

TDNNLSTM
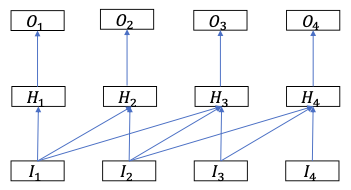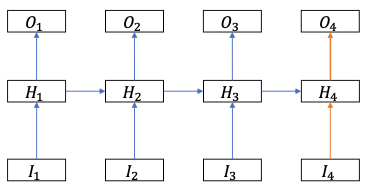截屏2020-08-21 12.37.38截屏2020-08-21 12.37.53
For $t = 1,\dots, T$:
$H\_{t}=\mathrm{f}\left(\mathrm{W}\_{1} \mathrm{I}\_{\mathrm{t}-\mathrm{D}}+\mathrm{W}\_{2} \mathrm{I}\_{\mathrm{t}-\mathrm{D}+1}+\mathrm{W}\_{3} \mathrm{I}\_{\mathrm{t}-\mathrm{D}+2}+\cdots+W\_{D} I_{t}\right)$		For $t = 1,\dots, T$:
$H\_{t}=f\left(W^{I} I\_{t}+W^{H} H\_{t-1}+b\right)$
Weights are shared over time?YesYes
Handle variable length sequences
  • Increasing long-range dependency learning by increasing $D$
  • Increasing $D$ also increases number of parameters
    		• Can flexibly adapt to variable length sequences without changing structures
    Gradient vanishing or exploding problem?NoYes
    Parallelism?Can be parallelized into 𝑂(1)
    (Assuming Matrix multiplication cost is O(1) thanks to GPUs…)    		Sequential computation
    (because $𝐻\_𝑇$ cannot be computed before $𝐻\_{𝑇−1}$)