Docs
AI
ML
Classification
K Nearest Neighbors

K Nearest Neighbors

Non-parametric Methods

  • Store all the training data
  • Use the training data for doing predictions
  • Do NOT adapt parameters
  • Often referred to as instance-based methods

👍 Advantages

  • Complexity adapts to training data
  • Very fast at training

👎 Disadvantages

  • Slow for prediction
  • Hard to use for high-dimensional input

$k$-Nearest Neighbour Classifiers

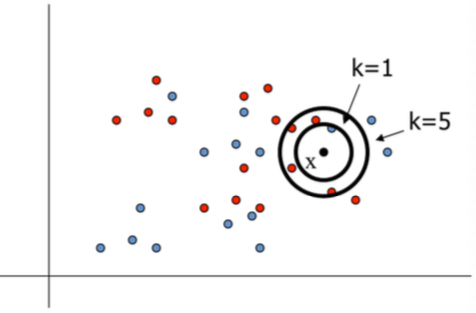
To classify a new input vector $x,$

  1. Examine the $k$-closest training data points to $x$ (comman values for $k$: $k=3$, $k=5$)
  2. Assign the object to the most frequently occurring class

image-20200128213429949

🤔 When to consider?

  • Can measure distances between data-points
  • Less than 20 attributes per instance
  • Lots of training data

👍 Advantages

  • Training is very fast
  • Learn complex target functions
  • Similar algorithm can be used for regression
  • High accuracy
  • Insensitive to outliers
  • No assumptions about data

👎 Disadvantages

  • Computationally expensive
  • requires a lot of memory

Decision Boundaries

  • The nearest neighbour algorithm does NOT explicitly compute decision boundaries.
  • The decision boundaries form a subset of the Voronoi diagram for the training data.
  • The more data points we have, the more complex the decision boundary can become

Distance Metrics

Most common distance metric: Euclidean distance (ED)

$$ d(\boldsymbol{x}, \boldsymbol{y})=\|\boldsymbol{x}-\boldsymbol{y}\|=\sqrt{\left(\sum_{k=1}^{d}\left(\boldsymbol{x}_{k}-\boldsymbol{y}_{k}\right)^{2}\right)} $$

  • makes sense when different features are commensurate; each is variable measured in the same units.

  • If the units are different (e.g.. length and weight), data needs to be normalised (resulting input dimensions are zero mean, unit variance)

    $$ \tilde{\boldsymbol{x}}=(\boldsymbol{x}-\boldsymbol{\mu}) \oslash \boldsymbol{\sigma} $$
    • $\mu$: Mean
    • $\sigma$: Standard deviation
    • $\oslash$: element-wise division

Another distance metrics:

  • Cosine Distance: Good for documents, images $$ d(\boldsymbol{x}, \boldsymbol{y})=1-\frac{\boldsymbol{x}^{T} \boldsymbol{y}}{\|\boldsymbol{x}\|\|\boldsymbol{y}\|} $$

  • Hamming Distance: For string data / categorical features $$ d(\boldsymbol{x}, \boldsymbol{y})=\sum_{k=1}^{d}\left(\boldsymbol{x}_{k} \neq \boldsymbol{y}_{k}\right) $$

  • Manhattan Distance: Coordinate-wise distance $$ d(\boldsymbol{x}, \boldsymbol{y})=\sum_{k=1}^{d}\left|\boldsymbol{x}_{k}-\boldsymbol{y}_{k}\right| $$

  • Mahalanobis Distance: Normalized by the sample covariance matrix – unaffected by coordinate transformations $$ d(\boldsymbol{x}, \boldsymbol{y})=\|\boldsymbol{x}-\boldsymbol{y}\|_{\Sigma^{-1}}=\sqrt{(\boldsymbol{x}-\boldsymbol{y})^{T} \boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{y})} $$