Minimum Edit Distance

Definition

Minimum edit distance between two strings $:=$ the minimum number of editing operations (operations like insertion, deletion, substitution) needed to transform one string into another.

Example

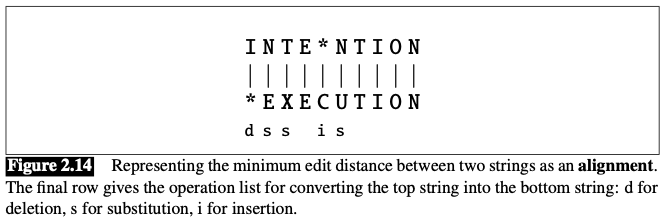
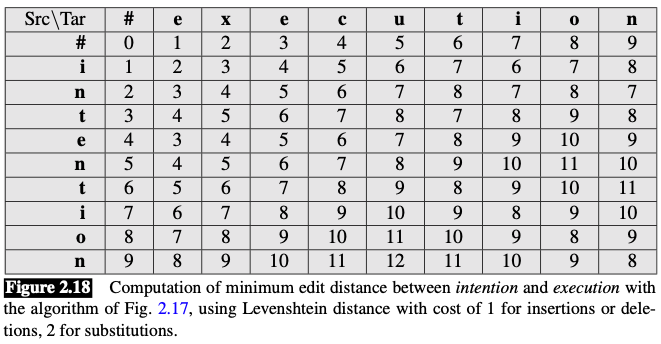
• The gap between intention and execution, for example, is 5 (delete an i, substitute e for n, substitute x for t, insert c, substitute u for n).

• Visualization

  

Levenshtein distance

Original version:

• Each of the three operations (insertion, deletion, substitution) has a cost of 1

• The substitution of a letter for itself (E.g., t for t), has zero cost.

• The Levenshtein distance between intention and execution is 5

Alternative version:

• Insertion or deletion has a cost of 1
• Substitution has a cost of 2 (since any substitution can be represented by one insertion and one deletion)
• Using this version, the Levenshtein distance between intention and execution is 8.

The Minimum Edit Distance Algorithm

How do we find the minimum edit distance?

💡 Think of this as a search task, in which we are searching for the shortest path—a sequence of edits—from one string to another.

• Just remember the shortest path to a state each time we saw it.
  • We can do this by using dynamic programming

Dynamic programming

• 💡 Intuition: a large problem can be solved by properly combining the solutions to various sub-problems

• Apply a table-driven method to solve problems by combining solutions to sub-problems

• Example: Consider the shortest path of transformed words that represents the minimum edit distance between the strings intention and execution

  

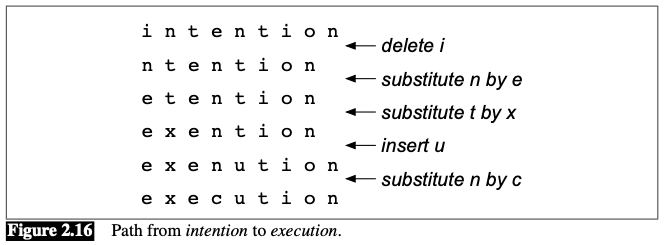
  Imagine some string (perhaps it is exention) that is in this optimal path (whatever it is). The intuition of dynamic programming is that if exention is in the optimal operation list, then the optimal sequence must also include the optimal path from intention to exention. Why? If there were a shorter path from intention to exention, then we could use it instead, resulting in a shorter overall path, and the optimal sequence wouldn’t be optimal, thus leading to a contradiction.

Minimum Edit Distance Algorithm

Define the minimum edit distance between two string

• Given:
  • Source string $X$ of length $n$
  • Target string $Y$ of length m
• $D[i, j]:=$ edit distance between $X[1..i]$ and $Y[1..j]$ (the first $i$ characters of $X$ and the first $j$ characters of $Y$)
• Thus, The edit distance between $X$ and $Y$ is $D[n, m]$

We’ll use dynamic programming to compute $D[n, m]$ bottom up, combining solutions to subproblems.

• Base case:

  • source substring of length $i$ but an empty target string, going from $i$ characters to 0 requires $i$ deletes.
  • target substring of length $j$ but an empty source going from 0 characters to $j$ characters requires $j$ inserts

• Having computed $D[i,j]$ for small $i, j$ we then compute larger $D[i,j]$ based on previously computed smaller values. The value of is$D[i,j]$ computed by taking the minimum of the three possible paths through the matrix which arrive there:

  

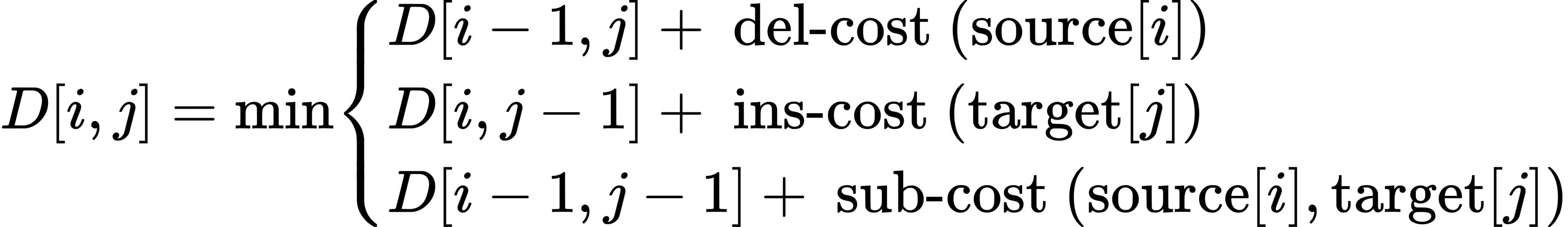
  If we assume the version of Levenshtein distance in which the insertions and deletions each have a cost of 1 ($\text { ins-cost }(\cdot)=\operatorname{del-cost}(\cdot)=1$), and substitutions have a cost of 2 (except substitution of identical letters have zero cost), the computation for $D[i,j]$ becomes:

  

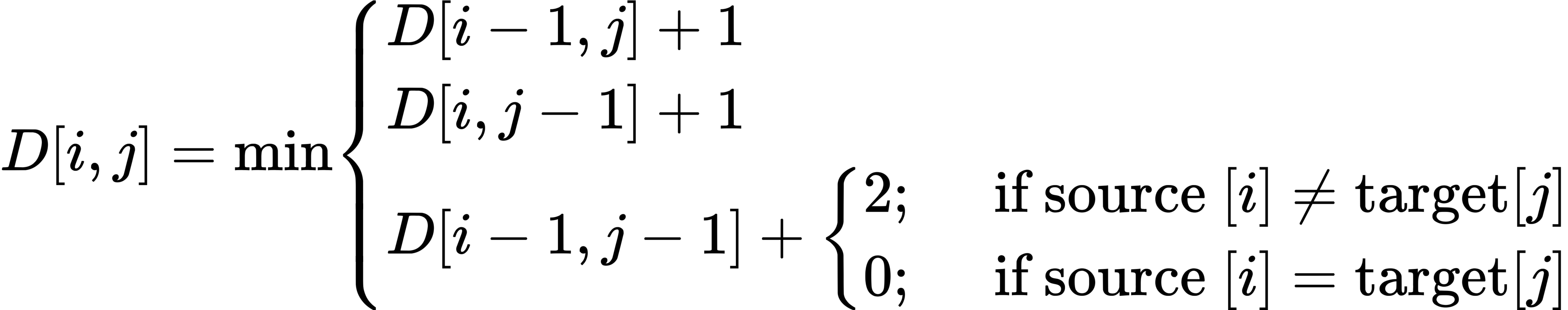
Pseudocode

Example

Minimum Cost Alignment

With a small change, the edit distance algorithm can also provide the minimum cost alignment between two strings.

To extend the edit distance algorithm to produce an alignment, we can start by visualizing an alignment as a path through the edit distance matrix.

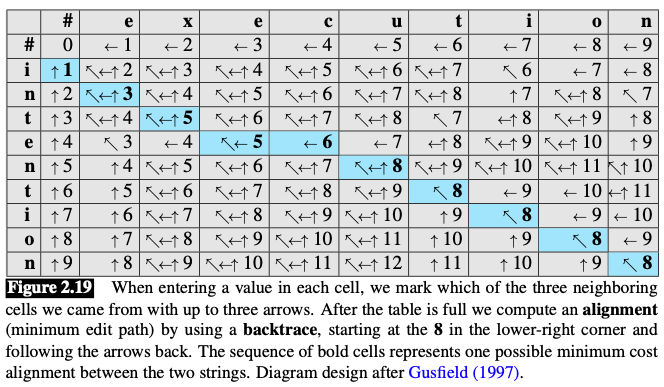
• Boldfaced cell: represents an alignment of a pair of letters in the two strings.
  • If two boldfaced cells occur in the same row, there will be an insertion in going from the source to the target
  • two boldfaced cells in the same column indicate a deletion.

Computation:

1. we augment the minimum edit distance algorithm to store backpointers in each cell.
   • The backpointer from a cell points to the previous cell (or cells) that we came from in entering the current cell.
   • Some cells have mul- tiple backpointers because the minimum extension could have come from multiple previous cells.
2. we perform a backtrace.
   • we start from the last cell (at the final row and column), and follow the pointers back through the dynamic programming matrix. Each complete path between the final cell and the initial cell is a minimum distance alignment.