Recursion
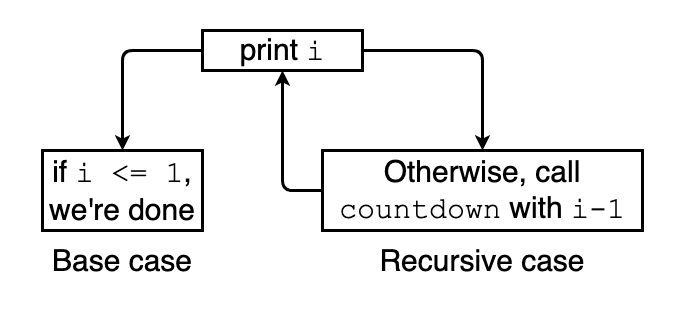
Every recursive function has two parts
- base case: the function does not call itself again, so it will not go into an infinite loop
- recursive case: the function calls itself
Sometimes recursion could be also re-written using loops. In fact, loops are sometimes better for performance. But recursion is used when it makes the solution clearer.
Examples
Count down
def countdown(i):
print(i)
if i <= 0: # base case
return
else: # recursive case
countdown(i-1)
countdown(5)
5
4
3
2
1
0
Factorial
factorial(3) is defined as $3! = 3 \cdot 2 \cdot 1 = 3$
def factorial(x):
# base case
if x == 1:
return 1 # 1! = 1
else:
return x * factorial(x-1)
factorial(3)
6
factorial(5)
120
Divide and Conquer
Divide and conquer (D&C) is a well-known recursive technique for solving problems. To solve a problem using D&C, there’re 2 steps:
- Figure out the base case. This should be the simplest possible case.
- Divide or decrease the problem until it becomes the base case.
Sum of Array
Let’s calculate the sum of an array using D&C.
Figure out the base case.
Base case is that the array is empty. In this situation, sum of this array is 0.
Decrease the problem until it becomes the base case.
sum = a[0] + a[1] + a[2] = a[0] + (a[1] + a[2]) = a[0] + (a[1] + (a[2] + 0))
Example:
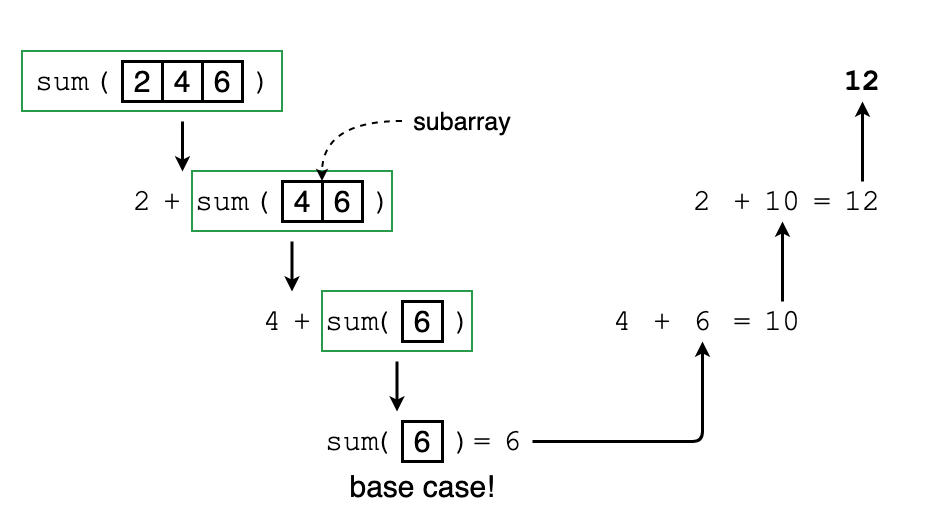
As we can see, in the 2nd and 3rd step, we’re passing a smaller (sub)array into the sum function. That is, we’re decreasing the size of our problem!
When we have figured out the two steps of D&C, the implementation is pretty simple:
def sum(arr):
if not arr: # arr is empty
return 0
else:
return arr[0] + sum(arr[1:])
Count Number of Elements
def length(arr):
if not arr:
# base case: length of empty array is 0
return 0
# recursive case: 1 + length of the remaining subarray
return 1 + length(arr[1:])
Find Maximum
def max(arr):
if len(arr) == 2:
return arr[0] if arr[0] > arr[1] else arr[1]
return arr[0] if arr[0] > max(arr[1:]) else max(arr[1:])
Recursive Binary Search
def binary_search(arr, low, high, target):
if low <= high:
mid = (low + high) // 2
if arr[mid] > target:
# If element is smaller than mid,
# then it can only be present in left subarray
return binary_search(arr, low, mid-1, target)
elif arr[mid] == target:
return mid
else:
# If element is greater than mid,
# then it can only be present in right subarray
return binary_search(arr, mid+1, high, target)
else: # Element is not present in the array
return -1