Hash Table
Hash Table
The Hash table data structure stores elements in key-value pairs where
- Key - unique integer that is used for indexing the values
- Value - data that are associated with keys.
Hash table is also called hash map, map, dictionary, and associative arrays.
Python has built-in hash tables, they’re called dictionary. E.g. we model a dictionary, where key and value correspond to fruit and price, respectively.
catalog = dict() # we use fruit name as key, and price as value
catalog["apple"] = 1.5
catalog["watermelon"] = 3.2
catalog["banana"] = 3
print(catalog)
{'apple': 1.5, 'watermelon': 3.5, 'milk': 3}
Hash Functions (Hashing)
In a hash table, a new index is processed using the key. And the value corresponding to that key is stored in this index. This process is called hashing.
Let $k$ be a key and $h(x)$ be a hash function. $h(k)$ will give us a new index in the table to store the value linked with $k$.
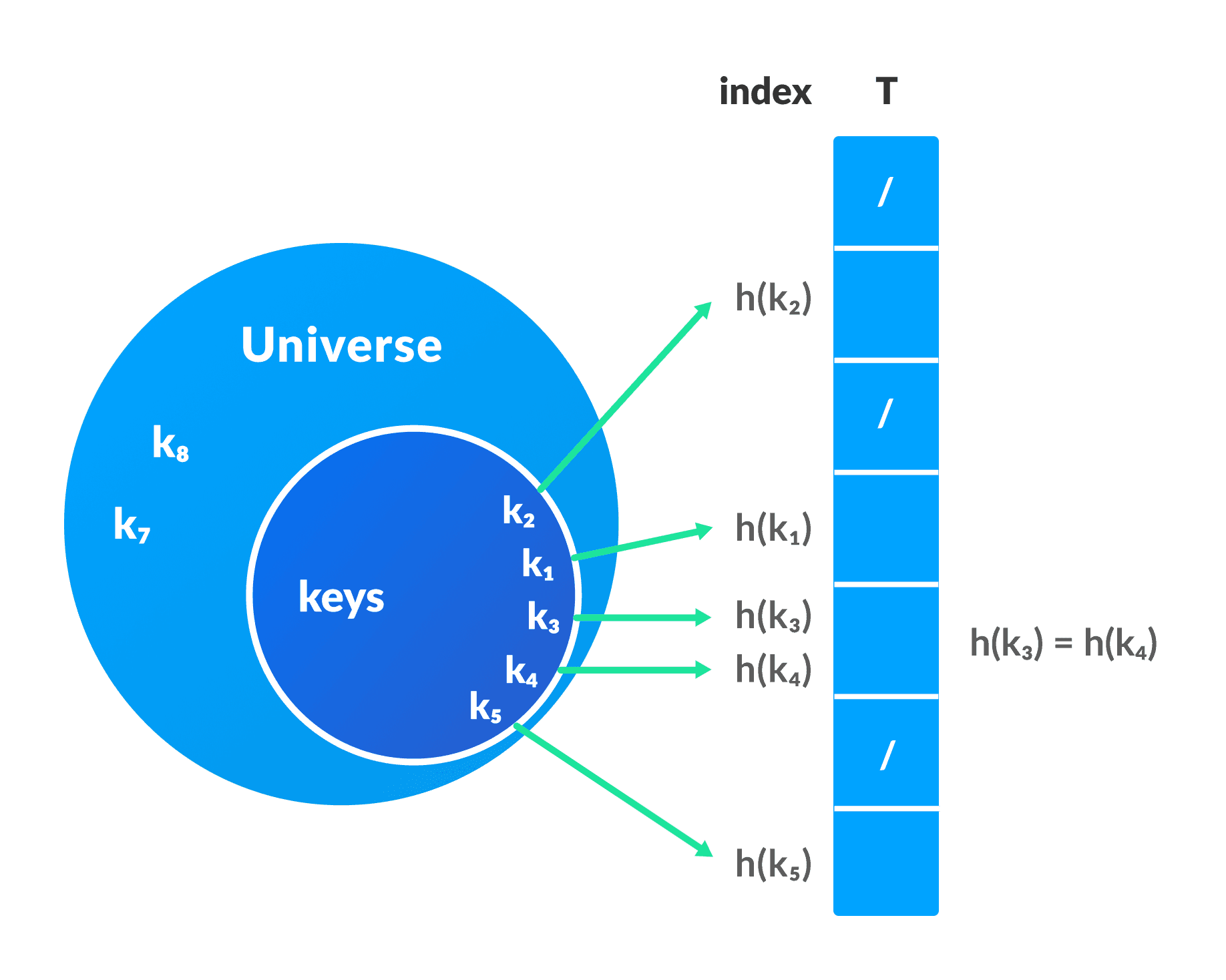
Requirements of a hash function:
- Consistent. Every time we input the same key, we should get the same index.
- Different keys should be mapped to different indexes.
Example
In the example above, let’s say for apple:
hash_function("apple") = 4
Therefore, the price of apple, 1.5, will be stored in table[4].
When we want to retrieve the price of apple (catalog.get("apple")), the hash function will tell us that its price is stored in the index 4 in table. So table[4] will be returned.
Hash Colliison
When the hash function generates the same index for multiple keys, there will be a conflict (what value to be stored in that index). This is called a hash collision.
We can resolve the hash collision using one of the following techniques.
Collision resolution by chaining
In chaining, if a hash function produces the same index for multiple elements, these elements are stored in the same index by using a doubly-linked list.
If j is the slot for multiple elements, it contains a pointer to the head of the list of elements.
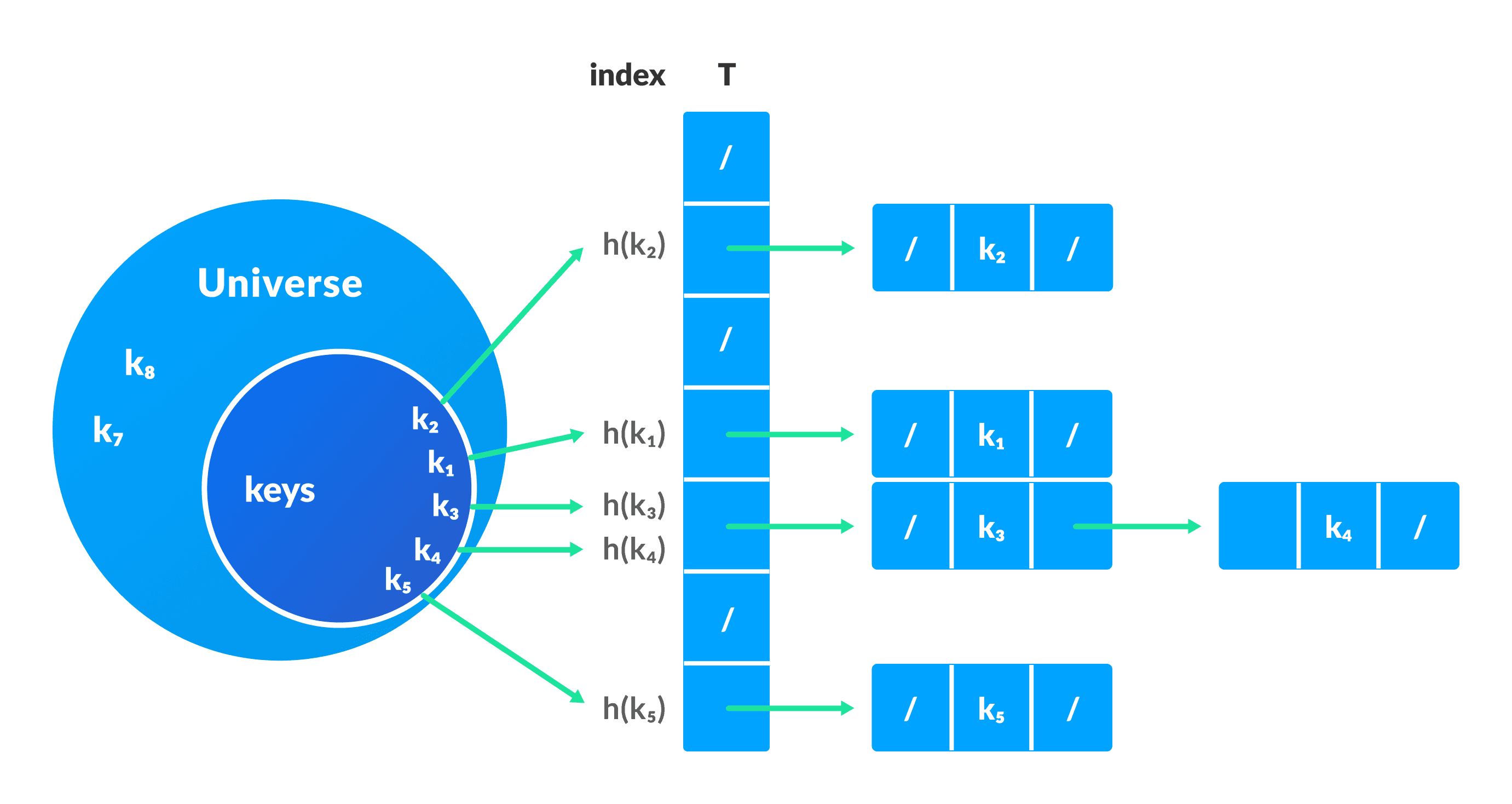
Open Addressing
Linear Probing
In linear probing, collision is resolved by checking the next slot.
$$ h(k, i) = (h^{\prime}(k) + i) \mod m $$where
$i = \{0 ,1, ...\}$
$h^{\prime}(k)$ is a new hash function.
Quadratic Probing
It works similar to linear probing but the spacing between the slots is increased (greater than one) by using the following relation.
$$ h(k, i) = (h^{\prime}(k) + c\_1 i + c\_2 i^2) \mod m $$where
$i = \{0 ,1, ...\}$
$c\_1$ and $c\_2$ are positive auxiliary constants
Double Hashing
If a collision occurs after applying a hash function h(k), then another hash function is applied for finding the next slot.
Avoid Hash Collision
To avoid hash collisions, we need
- a low load factor
- a good hash function
Load Factor
Load factor of a hash table is defined as
$$ \text{load factor} = \frac{\text{number of items in hash table}}{\text{total number of slots}} $$For example
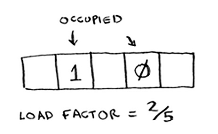
Having a load factor greater than 1 means you have more items than slots in your array. Once the load factor starts to grow, you need to add more slots to your hash table. This is called resizing. With a lower load factor, you’ll have fewer collisions, and your table will perform better.
Rule of thumb
Resize when load factor is greater than 0.7
Make an array that is twice the size.
Good Hash Function
A good hash function distributes values in the array evenly. It can reduce the number of collisions.
We have different methods to find a good hash function (Let $k$ be a key and m be the size of the hash table):
Division method
$$ h(k) = k \mod m $$Multiplication Method
$$ h(k) = \lfloor m(kA \mod 1)\rfloor $$- $\lfloor \rfloor$ gives the floor value
- $A \in (0, 1)$. $kA \mod 1$ gives the fractional part of $kA$. A suggested optimal choice for $A$ is $\frac{\sqrt{5} - 1}{2}$
Performance
Best case
The hash function maps keys evenly all over the hash table. In this case, hash table takes $O(1)$ for everything.
Worst case
The hash function maps all keys to the SAME index. In this case, hash table takes $O(n)$ for everything.
Comparison with Arrays and Linked Lists
| Hash table (average) | Hash table (worst) | Array | Linked list | |
|---|---|---|---|---|
| Search | $O(1)$ | $O(n)$ | $O(1)$ | $O(n)$ |
| Insert | $O(1)$ | $O(n)$ | $O(n)$ | $O(1)$ |
| Delete | $O(1)$ | $O(n)$ | $O(n)$ | $O(1)$ |