Pattern Recognition
Why pattern recognition and what is it?
What is machine learning?
- Motivation: Some problems are very hard to solve by writing a computer program by hand
- Learn common patterns based on either
a priori knowledge or
on statistical information
- Important for the adaptability to different tasks/domains
- Try to mimic human learning / better understand human learning
- Machine learning is concerned with developing generic algorithms, that are able to solve problems by learning from example data
Classifiers
Given an input pattern , assign in to a class
- Example: Given an image, assign label “face” or “non-face”
- : can be an image, a video, or (more commonly) any feature vector that can be extracted from them
- : desired (discrete) class label
- If “class label” is real number or vector –> Regression task
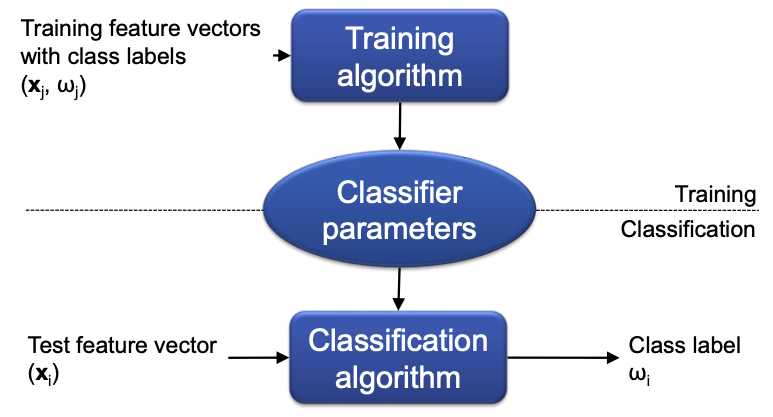
ML: Use example patterns with given class labels to automatically learn

Example
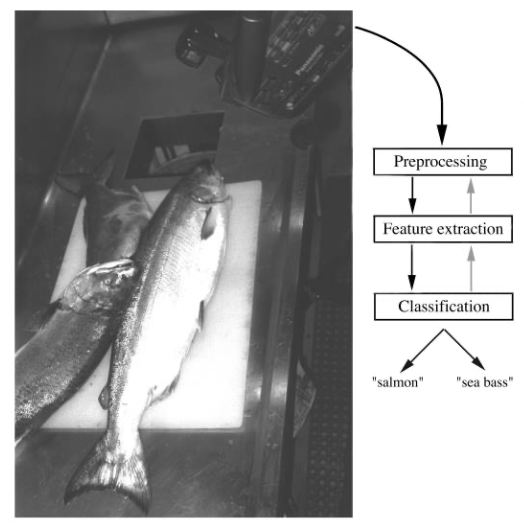
Classification process
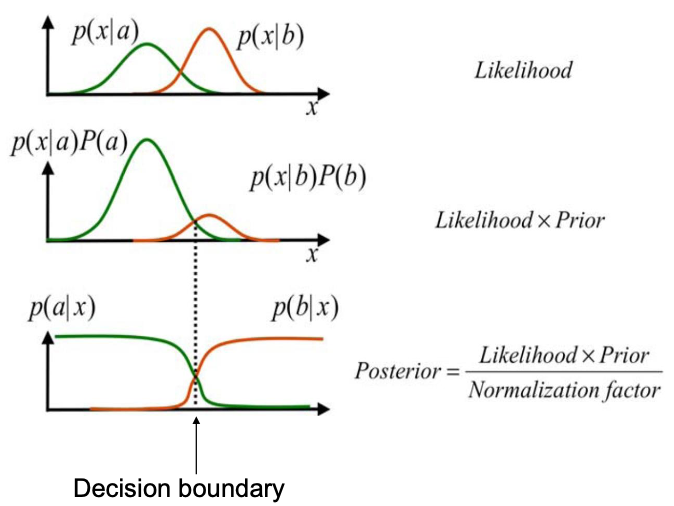
Bayes Classification
Given a feature vector , want to know which class is most likely
Use Bayes’ rule: Decide for the class with maximum posterior probability

🔴 Problem: (and to a lesser degree ) is usually unknown and often hard to estimate from data
Priors describe what we know about the classes before observing anything
Can be used to model prior knowledge
Sometimes easy to estimate (counting)
Example
Gaussian Mixture Models
Gaussian classification
Assumption:
- 👆 This makes estimation easier
- Only need to be estimated
- To reduce parameters, the covariance matrix can be restricted
Diagonal matrix –> Dimensions uncorrelated
Multiple of unit matrix –> Dimensions uncorrelated with same variance
- 👆 This makes estimation easier
🔴 Problem: if the assumption(s) do not hold, the model does not represent reality well 😢
Estimation of with Maximum (Log-)Likelihood
Use parameters, that best explain the data (highest likelihood):
–> Maimize over
Gaussian Mixture Models (GMMs)
Approximate true density function using a weighted sum of several Gaussians
Any density can be approximated this way with arbitrary precision
- But might need many Gaussians
- Difficult to estimate many parameters
Use Expectation Maximization (EM) Algorithm to estimate parameters of the Gaussians as well as the weights
Initialize parameters of GMM randomly
Repeat until convergence
Expectation (E) step:
Compute the probability that data point belongs to Gaussian
- Take the value of each Gaussian at point and normalize so they sum up to one
Maximization (M) step:
Compute new GMM parameters using soft assignments
- Maximum Likelihood with data weighted according to
parametric vs. non-parametric
Parametric classifiers
- assume a specific form of probability distribution with some parameters
- only the parameters need to be estimated
- 👍 Advantage: Need less training data because less parameters to estimate
- 👎 disadvantage: Only work well if model fits data
- Examples: Gaussian and GMMs
Non-parametric classifiers
Do NOT assume a specific form of probability distribution
👍 Advantage: Work well for all types of distributions
👎 disadvantage: Need more data to correctly estimate distribution
Examples: Parzen windows, k-nearest neighbors
generative vs. discriminative
- A method that models and explicitly is called a generative model
- allows to generate new samples of class
- The other common approach is called discriminative models
- directly model or just output a decision given an input pattern
- easier to train because they solve a simpler problem 👏
Linear Discriminant Functions
Separate two classes with a linear hyperplane
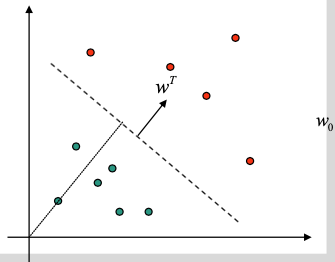
- Decide if else
- : normal vector of the hyperplane
Example:
- Perceptron (see: Perceptron)
- Linear SVM
Support Vector Machines
See: SVM
Linear SVMs
- If the input space is already high-dimensional, linear SVMs can often perform well too
- 👍 Advantages:
- Speed: Only one scalar product for classification
- Memory: Only one vector w needs to be stored
- Training: Training is much faster
- Model selection: Only one parameter to optimize
K-nearest Neighbours
💡 Look at the closest training samples and assign the most frequent label among them
Model consists of all training samples
Pro: No information is lost
Con: A lot of data to manage
Naïve implementation: compute distance to each training sample every time
- Distance metric is needed (Important design parameter!)
- , , , Mahalanobis, … or
- Problem-specific distances
- Distance metric is needed (Important design parameter!)
kNN often good classifier, but:
- Needs enough data
- Scalability issues
Clustering
- New problem setting
- Only data points are given, NO class labels
- Find structures in given data
- Generally no single correct solution possible
K-means
Algorithm
Randomly initialize k cluster centers
Repeat until convergence:
Assign all data points to closest cluster center
Compute new cluster center as mean of assigned data points
👍 Pros: Simple and efficient
👎 Cons:
- needs to be known in advance
- Results depend on initialization
- Does not work well for clusters that are not hyperspherical (round) or clusters that overlap
Very similar to the EM algorithm
- Uses hard assignments instead of probabilistic assignments (EM)
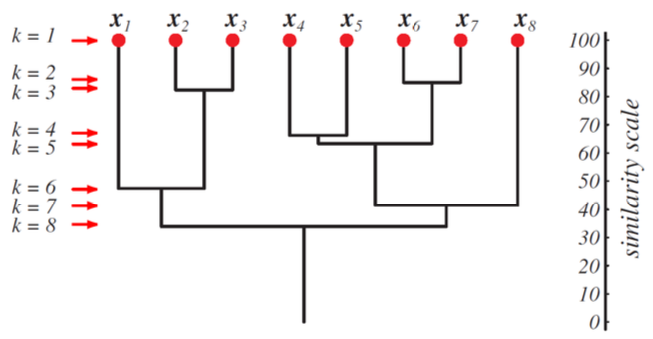
Agglomerative Hierarchical Clustering
Algorithm
Start with one cluster for each data point
Repeat
- Merge two closest clusters
Several possibilities to measure cluster distance
Min: minimal distance between elements
Max: maximal distance between elements
Avg: average distance between elements
Mean: distance between cluster means
Result is a tree called a dendrogram
Example:
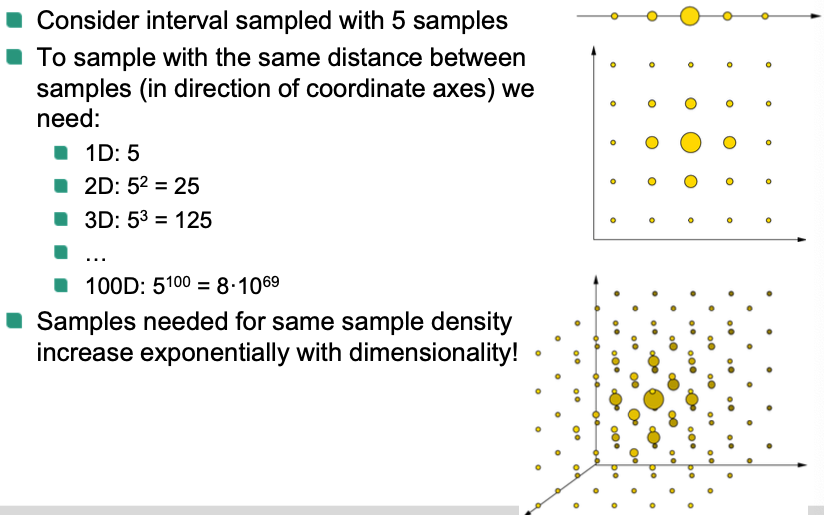
Curse of dimensionality
In computer vision, the extracted feature vectors are often high-dimensional
Many intuitions about linear algebra are no longer valid in high-dimensional spaces 🤪
- Classifiers often work better in low-dimensional spaces
These problems are called “curse of dimensionality" 👿
Example
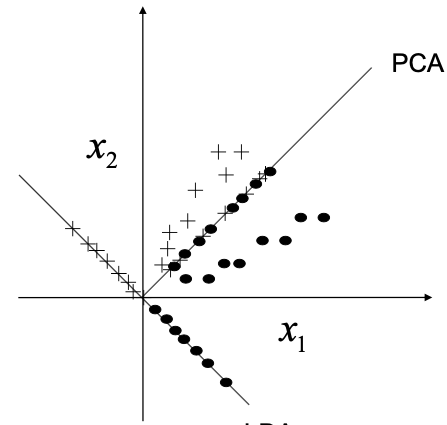
Dimensionality reduction
PCA: Leave out dimensions and minimize error made
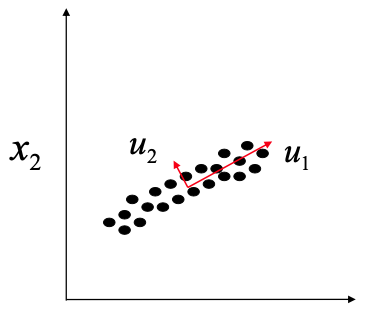
LDA: Maximize class separability