Face Detection: Color-Based

TL;DR

• Different color spaces and classifiers can be used

  • Models: histograms, Gaussian Models, Mixture of Gaussians Model

  • Histogram-backprojection / Histogram matching

  • Bayes classifier

  • Discriminative Classifiers (ANN, SVM)

• Bayesian classifier and ANN seem to work well

  • Sufficient training data is needed for modeling the pdf, in particular for Bayesian approach (positive & negative pdfs learned)

• Advantages: Fast, rotation & scale invariant, robust against occlusions

• Disadvantages:

  • Affected by illumination
  • Cannot distinguish head and hands
  • Skin-colored objects in the background problematic

• Metric: ROC curve used to compare classification results / methods

---

Color-based face detection overview

💡 Idea: human skin has consistent color, which is distinct from many objects

Possible approach:

1. Find skin colored pixels
2. Group skin colored pixels

• (and apply some heuristics) to find the face

Color

• Grayscale Image: Each pixel represented by one number (typically integer between 0 and 255)
• Color image: Pixels represented by three numbers

Different representations exist –> „Color Spaces“

Color spaces

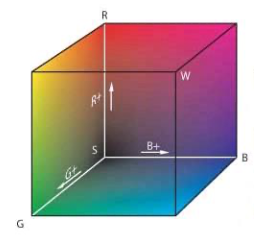
• RGB

  • most widely used

  • specifies colors in terms of the primary colors red (R), green (G), and blue (B)

    

• HSV/HSI: hue (H), saturation (S) and value(V)/intensity (I)

  • Closely related to human perception (hue, colorfulness and brightness)

    

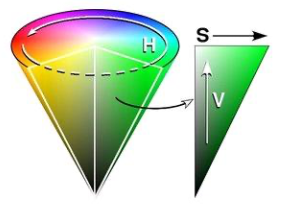
    • Hue: “color”
    • Saturation: How “pure” the color is?
    • Value: “lightness”

• Class Y spaces: YCbCr (Digital Video), YIQ (NTSC), YUV (PAL)

  • Y channel contains brightness, other two channels store chrominance (U=B-Y, V=R-Y)

  • Conversion from RGB to Yxx is a linear transformation

    

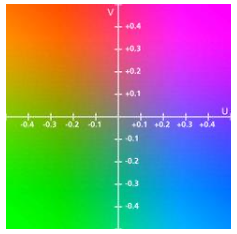
• Perceptually uniform spaces

  • Perceived color difference is uniform to difference in color values
  • Euclidian distance can be used for color comparison

  

• Chromatic Color Spaces

  • Two color channels containing chrominance (colour) information

    • HS (taken from HSV)
    • UV (taken from YUV)

  • Normalized rg from RGB:

    • r = R / (R+G+B)

    • g = G / (R+G+B)

    • b = B / (R+G+B)

  • Sometimes it is argued that chromatic skin color models are more robust

Problems

• Reflected color depends on spectrum of the light source (and properties of the object / surface)
• If the light source / illumination changes, the reflected color signal changes!!! 🤪

How to model skin color?

• Non-parametric models: typically histograms

• Parametric models

  • Gaussian Model
  • Gaussian Mixture Model

• Or just learn decision boundaries between classes (discriminative model)

  • ANN, SVM, …

Histogram as skin color model

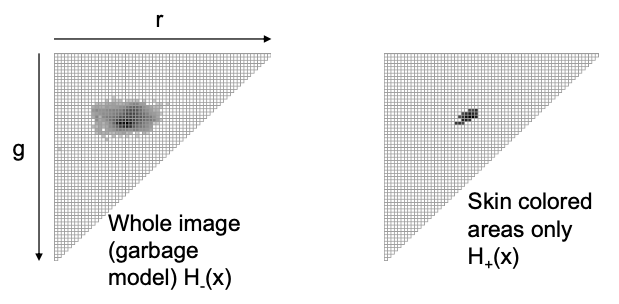
• 👍 Advantages: Works very well in practice
• 👎 Disadvantages
  • Memory size quickly gets high
  • A large number of labelled skin and non-skin samples is needed!

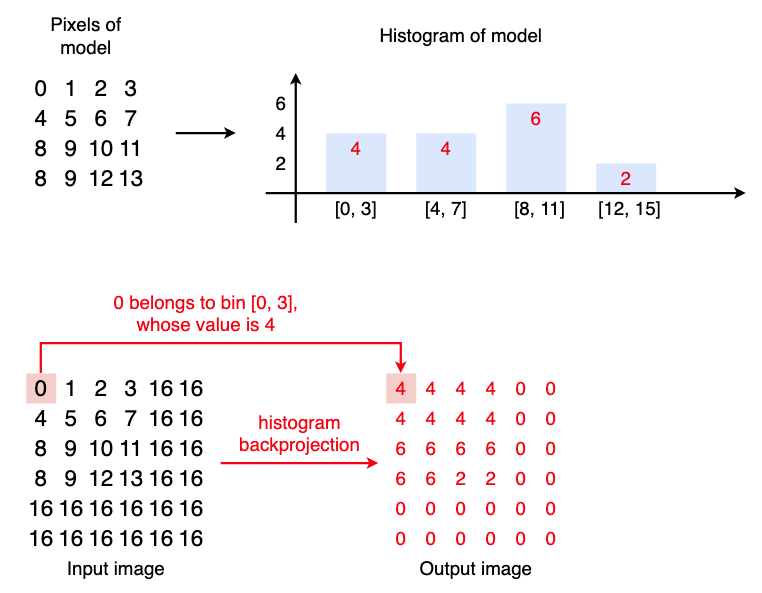
Histogram Backprojection

• The simplest (and fastest) way to utilize histogram information

• Each pixel in the backprojection is set to the value of the (skin-color) histogram bin indexed by the color of the respective pixel

  • A color $x$ is considered as skin color if $H\_{+}(x) > \theta$

• E.g.

  

Histogram Matching

• Backprojection
  • is good, when the color distribution of the target is monomodal.
  • is not optimal, when the target is multi colored! 😢
• 🔧 Solution: Build a histogram of the image within the search window, and compare it to the target histogram.
  • distance metrics for histograms, e.g.:

    • Battacharya distance

    • Histogram intersection

    • Earth-movers distance,…

Histogram Backprojection vs. Matching

• Histogram Backprojection

  • Compares color of a single pixel with color model

  • Fast and simple

  • Can only cope well with mono-modal distributions

  • sufficient for skin-color classification

• Histogram Matching / Intersection

  • Compares color histogram of image patch with color model

  • Better performance

  • Can cope with multi-modal distributions

  • Computationally expensive

Parametric models

Gaussian Density Models

• Gaussian Densities

  • Assume that the distribution of skin colors p(x) has a parametric functional form

  • Most common function: Gaussion function $\mathrm{G}(\mathbf{x} ; \mu, \mathbf{C})$

    $$ p(x | \text{skin})=G(x ; \mu, C)=\frac{1}{(2 \pi)^{d / 2}|C|^{1 / 2} }\exp \left\\{-1 / 2(x-\mu)^{\top} C^{-1}(x-\mu)\right\\} $$
    • Mean $\mu$ and covariance matrix $C$ are estimated from a training set of skin colors $S = {x\_1,x\_2,...,x\_N}$:
      • $\mu = E\{x\}$
      • $C = E\{(\boldsymbol{x}-\mu)^T(\boldsymbol{x}-\mu)\}$

  • A color is considered as skin color if

    • $p(x|\text{skin}) > \theta$
    • $p(x|\text{skin}) > p(x|\text{non-skin})$

Mixture of Gaussian Models

$$ p(x)=\sum\_{i=1}^{K} \pi\_{i} G\left(x, \mu\_{i}, C\_{i}\right) $$

• Parameter set $\Phi$ can be estimated using the EM algorithm

  • Iteratively changes parameters so as to maximize the log-likelihood of the training set: $$ L=\log \prod\_{i=1}^{N} p\left(x\_{i} \mid \Phi\right) $$

• A color is considered as skin color if

  • $p(x|\text{skin}) > \theta$
  • $p(x|\text{skin}) > p(x|\text{non-skin})$

Bayes Classifier

• Skin Classification using Bayes Decision Rule

  • Minimum cost decision rule

  • Classify pixel to skin class if $P(\text{Skin} | x)>P(\text{Non-Skin} | x)$

  • Decision Rule:

    $$ \frac{p(\mathbf{x} \mid \text {Skin})}{p(\mathbf{x} \mid \text {Non-Skin})} \geq \frac{P(\text {Non-Skin})}{P(\text {Skin})} $$

  • The classconditionals $p(x|\omega)$ can be estimated from the corresponding histograms:

    $$ p\left(x \mid \omega\_{i}\right)=h\_{i}(x) / \sum\_{x} h\_{i}(x) $$
    • $h\_i(x)$: count of pixels from class $\omega\_{i}$ that have value $x$

Discriminative Models / Classifiers

• Artificial Neural Networks
• Support Vector Machine

Performance Measures

For classification

When comparing recognition hypotheses with ground-truth annotations have to consider four cases:

More see: Evaluation

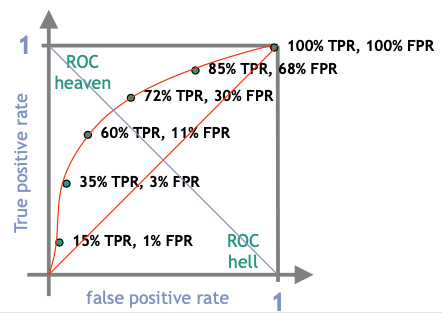
ROC (Receiver Operating Characteristic)

• Used for the task of classification
• Measures the trade-off between true positive rate and false positive rate

$$ \begin{array}{l} \text { true positive rate }=\frac{\mathrm{TP}}{\mathrm{Pos}}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}} \\\\ \text { false positive rate }=\frac{\mathrm{FP}}{\mathrm{Neg}}=\frac{\mathrm{FP}}{\mathrm{FP}+\mathrm{TN}} \end{array} $$

• Each prediction hypothesis has generally an associated probability value or score

• The performance values can therefore plotted into a graph for each possible score as a threshold

• Example:

  

Skin-color: Analysis and Comparison

Conclusions ¹

• Bayesian approach and MLP worked best

  • Bayesian approach needs much more memory

• Approach is largely unaffected by choice of color space, but

• Results degraded when only chrominance channels were used

From Skin-Colored Pixels to Faces

• Skin-colored pixels need to be grouped into object representations

  

• 🔴 Problems:

  • skin-colored background,
  • further skin-colored body parts (hands, arms, …),
  • Noise, …

Perceptual Grouping

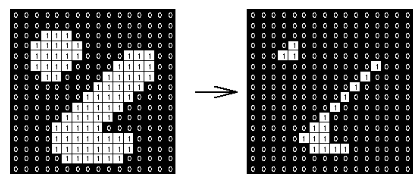
• Morphological Operators: Operators performing an action on shapes where the input and output is a binary image.

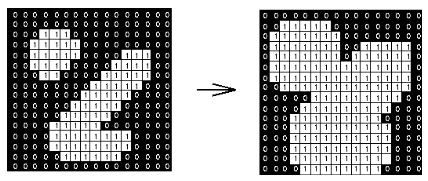
• Threshold each pixel‘s skin affiliation –> Binary Image

  

• Morphological Erosion

  • Remove pixels from edges of objects

  • Set pixel value to min value of surrounding pixels

    

• Morphological Dilatation

  • Add pixels to edges of objects

  • Set pixel value to max value of surrounding pixels

    

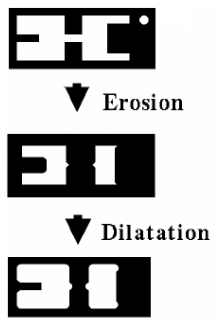
• Morphological Opening

  • Apply erosion, then dilatation

    

  • Goal:

    • Smooth outline
    • Open small bridges
    • Eliminate outliers

• Morphological Closing

  • Apply dilatation, then erosion

    

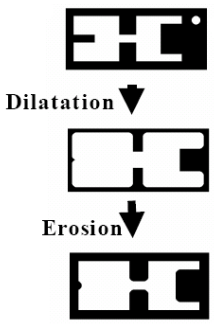
  • Goal:

    • Smooth inner edges
    • Connect small distances
    • Fill unwanted holes

• Apply morphological closing then morphological opening

  • Resulting image is reduced to connected regions of skin color (blobs)

    

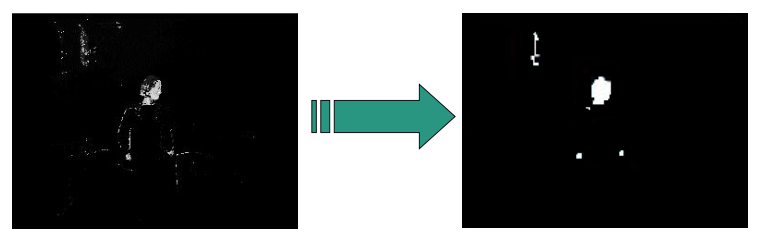
From Skin Blobs To Faces

• Goal: align bounding box around face candidate

  

• Important for:

  • Face Recognition

  • Head Pose Estimation

• Different approaches:

  • Choose cluster with biggest size

  • Ellipse fitting (approximate face region by ellipse)

  • Heuristics to distinguish between different skin clusters

  • Use temporal information (tracking)

  • Facial Feature Detection

  • …