Tracking

Introduction

Tracking Vs. Detection

• Detection: Find an object in a single image

  • Face, person, body part, facial landmarks, …
  • No assumption about dynamics, temporal consistency made

• Tracking:

  • determine a target’s locations (and/or rotation, deformation, pose, …) over a sequence of images

    i.e.: determine the target’s state (location and/or rotation, deformation, pose, …) over a sequence of observations derived from images

  • Provides object positions (etc.) in each frame

Motivation

• Use more than one image to analyse the scene
• Use a-priori knowledge to improve analysis
  • system dynamics, imaging / measurment process,

Target types

• Single objects: face, person, …
• Multiple objects: group of people, head and hands, …
• Articulated body: full body, hand

Sensor setup

• Single camera
• Multiple cameras
• Active cameras
• Cameras + microphones

observations used for tracking

• Templates
• Color
• Foreground-Background segmentation Edges
• Dense Disparity
• Optical flow
• Detectors (body, body parts)

Tracking as State Estimation

• Want to predict state of the system (position, pose, …)
  • But state cannot directly be measured
• Only certain observations (measurements) can be made
  • But Observations are noisy! (due to measurement errors)

What is the most likely state $x$ of the system at a given time, given a sequence of observations $Z\_t$ ?

• $x\_t$: state of the system at time $t$

• $z\_t$: Observation / measurement about the certain aspects of the system at

  time $t$

• Observations up to time $t$: $z\_{1:t}$ or $Z\_t$

Bayes Filter

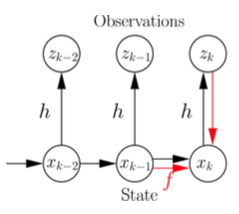
• Assume state $x$ to be Markov process

  $$p\left(x\_{t} \mid x\_{t-1}, x\_{t-2}, . ., x\_{0}\right)=p\left(x\_{t} \mid x\_{t-1}\right)$$

• States $x$ generate observations $z$

  $$p\left(z\_{t} \mid x\_{t}, x\_{t-1}, . ., x\_{0}\right)=p\left(z\_{t} \mid x\_{t}\right)$$

• Want to estimate most likely state $x\_t$ given sequence $Z\_t$:

  $$\arg \max p\left(x\_{t} \mid Z\_{t}\right)$$

• Can be estimated recursively

  

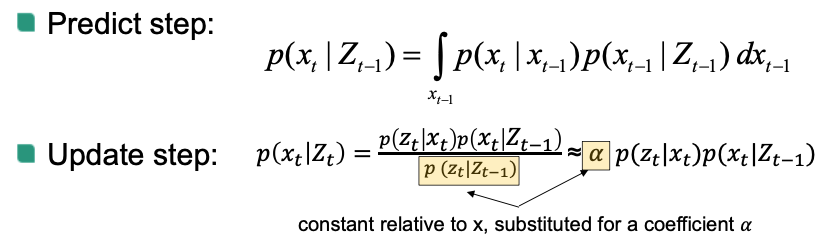
• Need:

  • Process model: $p(x\_t | x\_{t-1})$
  • Measurement model: $p(z\_t | x\_t)$

Helpful resource:

• Bayes Filters
• 概率机器人——贝叶斯滤波

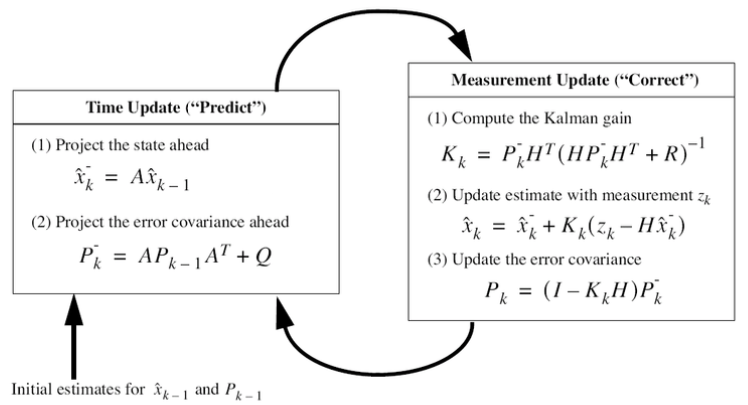
Kalman filter

• An instance of a Bayes filter
• Assumes
  • Linear state propagation and measurement model
  • Gaussian process and measurement noise

The process to be estimated:

• $x\_k$: state at time $k$
• $A$: transition matrix
• $z\_k$: obeservation at time $k$
• $H$: measurement matrix
• $p(w) \sim N(0, Q)$: process noise
• $p(v) \sim N(0, R)$: measurement noise

Note:

• The simple Kalman Filter is NOT applicable, when the process to be estimated is NOT linear or the measurement relationship to the process is NOT linear.

  $\rightarrow$ The Extended Kalman Filter (EKF) linearizes about the current mean and covariance

Paticle Filter

Helpful resources:

• Particle Filters Basic Idea

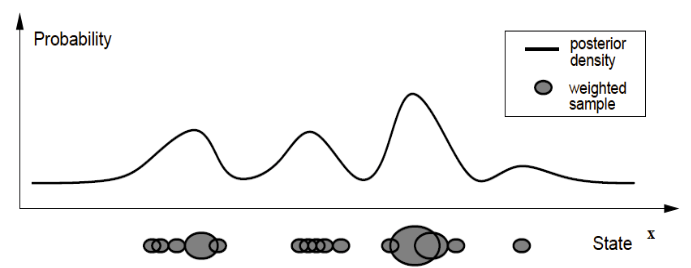
• The Kalman Filter often fails when the measurement density is multimodal / non-Gaussian.
• A Particle Filter represents and propagates arbitrary probability distributions. They are represented by a set of weighted samples.
  • The Particle Filtering is a numerical technique (unlike the Kalman filter which is analytical).
  • Like a Kalman Filter, a Particle Filter incorporates a dynamic model describing system dynamics

Bayesian Tracking

Bayes rule applied to tracking

Simplifying assumption (Markov):

where

• $x\_t$: state at time $t$
• $z\_t$: observation at time $t$
• $X\_t$: history of states up to the time $t$
• $Z\_t$: history of observations up to $t$

Observation and Motion Model

• $p(z\_t | x\_t)$: The likelihood that the $z\_t$ is observed, given that the true state of the system is represented by $x\_t$
• $p(x\_{t} | x\_{t-1})$: The likelihood that the state of the system is $x\_t$ when the previous state was $x\_{t-1}$

Factored Sampling

Probability density function is represented by weighted samples (“particles“)

Particle Filter (PF)

For a PF tracker, you need

• a set of $N$ weighted samples (particle) at time $k$

  \left\\{\left(s\_{k}^{(i)}, \pi\_{k}^{(i)}\right) \mid i=1 \dots N\right\\}

• the motion model

  $$s\_{k}^{(i)} \leftarrow s\_{k-1}^{(i)}$$

• the observation model

  $$\pi\_{k}^{(i)} \leftarrow s\_{k}^{(i)}$$

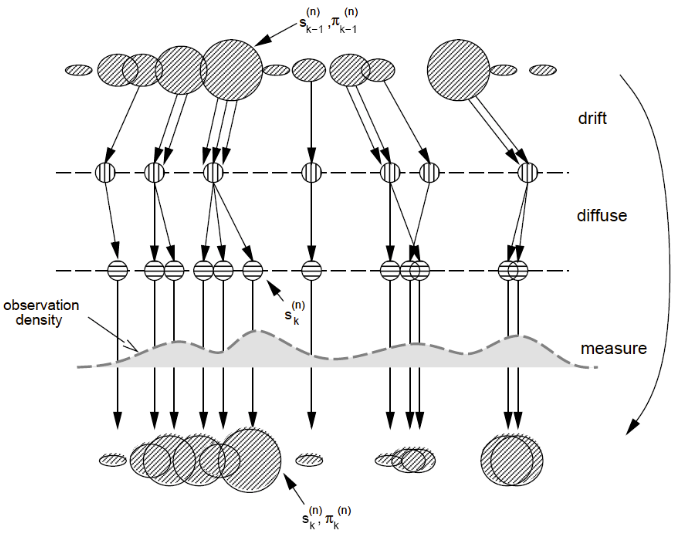
The Condensation Algorithm

A popular instance of a particle filter in Computer Vision

1. Select

   Randomly select $N$ new samples $S\_{k}^{(i)}$ from the old sample set $S\_{k-1}^{(i)}$ according to their weights $\pi\_{k-1}^{(i)}$

2. Predict

   Propagate the samples using the motion model

3. Measure

   Calculate weights for the new samples using the observation model

   $$\pi\_{k}^{(i)}=p\left(z\_{k} \mid x\_{k}=s\_{k}^{(i)}\right)$$

Illustration:

How to get the target position?

• Cluster the particle set and search for the highest mode
• Just take the strongest particle

How many particles are needed?

• Depends strongly on the dimension of the state space!
• Tracking 1 object in the image plane typically requires 50-500 particles

Problem

The Dimensionality Problem

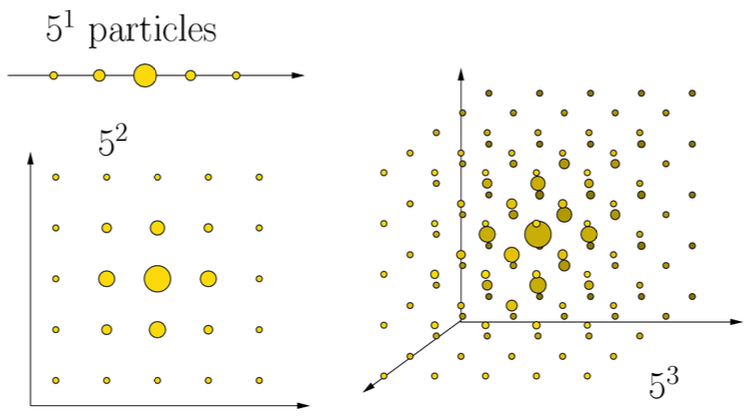
Examples

Tracking one Face with a Particle Filter

• State: ($x$, $y$, scale)

• Observations: skin color

• Procedure:

  1. Select and predict samples

  2. Measurement step

     • For each particle

       • Count supporting skin pixels in box defined by ($x$, $y$, scale)
       • Particle weights determined based on skin color support

     • Particle with maximum weight choosen as best solution

Tracking multiple objects

Two different approaches:

• A dedicated tracker for each of the objects
  • Start with one tracker, once an object is tracked, initialize one more tracker to search for more objects
  • Typically fast and well parallelizable
  • Optimal global assignment / tracking difficult to find, Information has to be shared across trackers to find a good assignment
• A single tracker in a joint state space
  • Easier to find optimal assignment
  • Number of objects has to be known in advance
  • State space becomes high dimensional (curse of dimensionality)

Face and Head Pose Tracking

• Particle filter: Head-pose estimation integrated in the tracker
• Observation model
  • Use bank of face detectors for different poses
  • Update particle weights with score of matching detector, i.e. the detector with closest angle to hypothesis
• Dynamical model: Gaussian noise, no explicit velocity model
• Occlusion handling
  • Set particle weight to zero, if it is too close to another track’s center