Docs
AI
CV
CV Lecture
Tracking 2

Tracking 2

Multi-Camera Systems

Type of multi-camera systems

  • Stereo-camera system (narrow baseline)

    ​

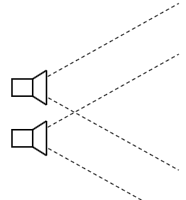
    截屏2021-07-20 17.13.58

    • Close distance and equal orientation
    • An object’s appearance is almost the same in both cameras
    • Allows for calculation of a dense disparity map

  • Wide-baseline multi-camera system

    ​

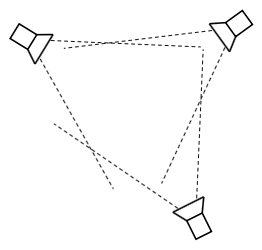
    截屏2021-07-20 17.15.59

    • Arbitrary distance and orientation, overlapping field of view

    • An object’s appearance is different in each of the cameras

      截屏2021-07-20 17.16.15

    • Allows for 3D localization of objects in the joint field of view

  • Multi-camera network

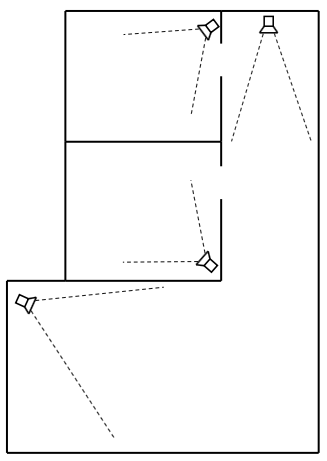
    ​ 截屏2021-07-20 17.16.55

    • Non-overlapping field of view
    • An object’s appearance differs strongly from one camera to another

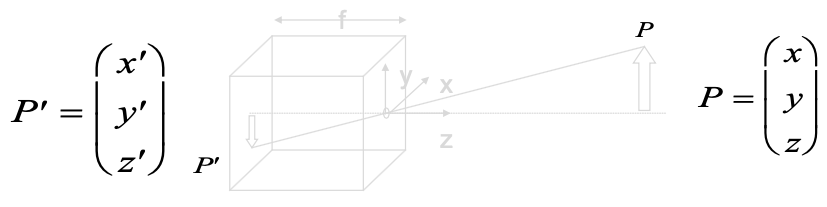
3D to 2D projection: Pinhole Camera Model

Summary:

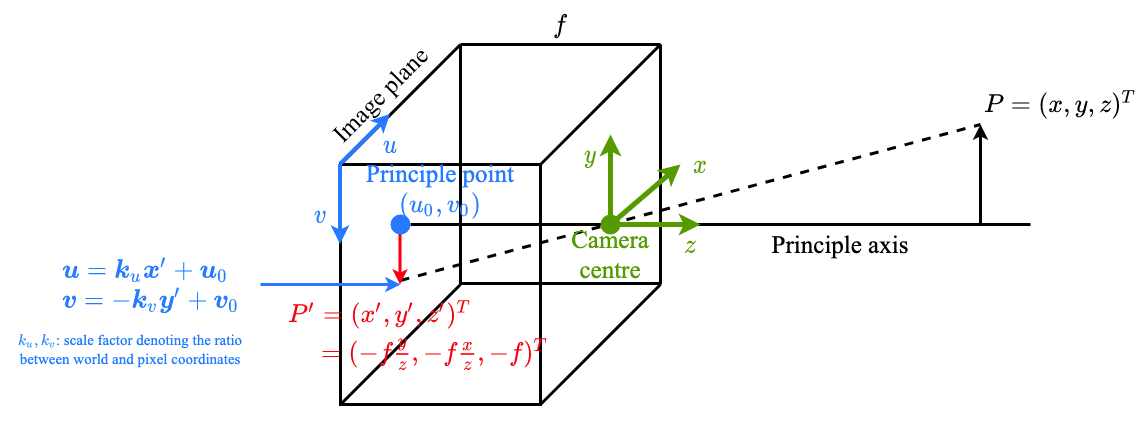
截屏2021-07-24 18.49.45

截屏2021-07-20 17.19.45

$$ z^{\prime} = -f $$ $$ \frac{y^{\prime}}{-f}=\frac{y}{z} \Rightarrow y^{\prime}=\frac{-f y}{z} $$ $$ \frac{x^{\prime}}{-f}=\frac{x}{z} \Rightarrow x^{\prime}=\frac{-f x}{z} $$

Pixel coordinates $(u, v)$ of the projected points on image plane

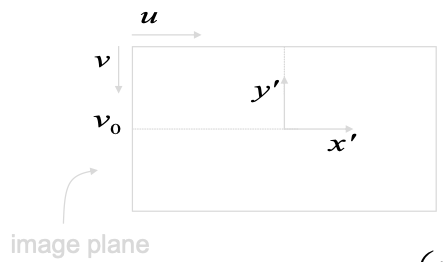
截屏2021-07-20 18.24.21

$$ \begin{array}{l} \boldsymbol{u}=\boldsymbol{k}\_{u} \boldsymbol{x}^{\prime}+\boldsymbol{u}\_{\mathrm{0}} \\\\ \boldsymbol{v}=-\boldsymbol{k}\_{v} \boldsymbol{y}^{\prime}+\boldsymbol{v}\_{\mathrm{0}} \end{array} $$

where $k\_u$ and $k\_v$ are scaling factors which denote the ratio between world and pixel coordinates.

In matrix formulation:

$$ \left(\begin{array}{l} u \\\\ v \end{array}\right)=\left(\begin{array}{cc} k\_{u} & 0 \\\\ 0 & -k\_{v} \end{array}\right)\left(\begin{array}{l} x^{\prime} \\\\ y^{\prime} \end{array}\right)+\left(\begin{array}{l} u\_{0} \\\\ v\_{0} \end{array}\right) $$

Perspective Projection

  • internal camera parameters

    $$ \begin{array}{l} \alpha\_{u}=k\_{u} f \\\\ \alpha\_{v}=-k\_{v} f \\\\ u\_{0} \\\\ v\_{0} \end{array} $$
    • have to be known to perform the projection
    • they depend on the camera only
    • Perform calibration to estimate

Calibration

Intrinsics parameters: describe the optical properties of each camera (“the camera model”)

  • $f$: focal length
  • $c\_x, c\_y$: the principal point (“optical center”), sometimes also denoted as $u\_0, v\_0$
  • $K\_1, \dots, K\_n$: distortion parameters (radial and tangential)

Extrinsic parameters: describe the location of each camera with respect to a global coordinate system

  • $\mathbf{T}$: translation vector
  • $\mathbf{R}$: $3 \times 3$ rotation matrix

Transformation of world coordinate of point $p^* = (x, y, z)$ to camera coordinate $p$:

$$ p = \mathbf{R} (x, y, z)^T + \mathbf{T} $$

Calibration steps

  1. For each camera: A calibration target with a known geometry is captured from multiple views
  2. The corner points are extracted (semi-)automatically
  3. The locations of the corner points are used to estimate the intrinsics iteratively
  4. Once the intrinsics are known, a fixed calibration target is captured from all of the camerasextrinsics

Triangulation

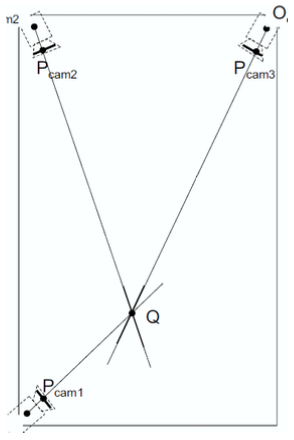
截屏2021-07-20 19.14.22

  • Assumption: the object location is known in multiple views
  • Ideally: The intersection of the lines-of-view determines the 3D location
  • Practically: least-squares approximation