Body Pose

Kinect

What is Kinect?

• Fusion of two groundbreaking new technologies
  • A cheap and fast RGB-D sensor
  • A reliable Skeleton Tracking

Structured light

• Kinect uses Structured Light to simulate a stereo camera system
• Kinect provides an unique texture for every point of the image, therefore only Block-Matching is required

Pose Recognition for User Interaction

Few constrains:

• Extremely low latency.
• Low computational power.
• High recognition rate, without false positives.
• Any personalized training step.
• Few people at once.
• Complex poses will be usual.

Pose Recognition¹

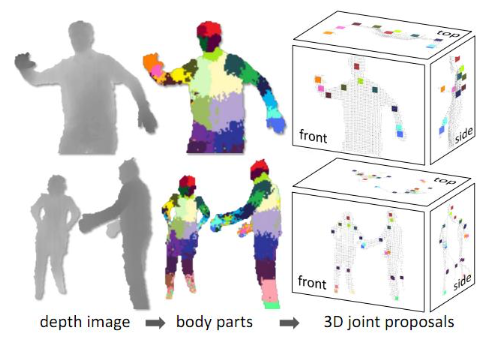
1st step: Pixel classification

Speed is the key

• Uses only one disparity image.

• It classifies each pixel independently.

• The process of feature extraction is simultaneous to the classification.

• Simplest possible feature: difference between two pixels.

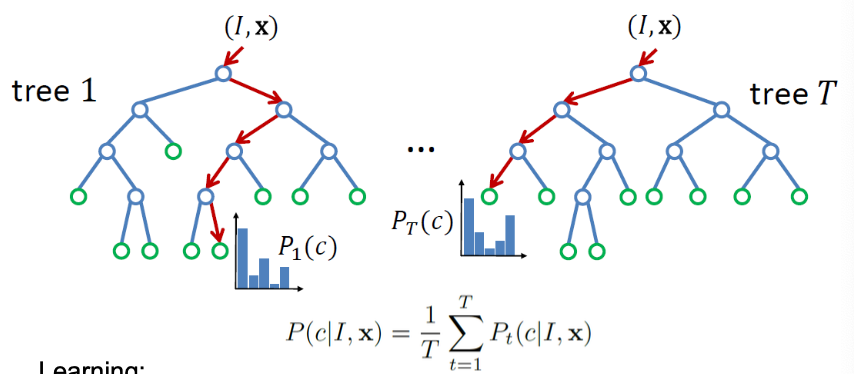
• Classification is done through Random Decision Forests.

  • Learning
    • Randomly choose a set of thresholds and features for splits.
    • Pick the threshold and feature that provide the largest information gain.
    • Recurse until a certain accuracy is reached or depth is obtained.
  

• Everything has an optimal GPU implementation.

Training

• Key: using a huge amount of training data

• Synthetic Training DB

  

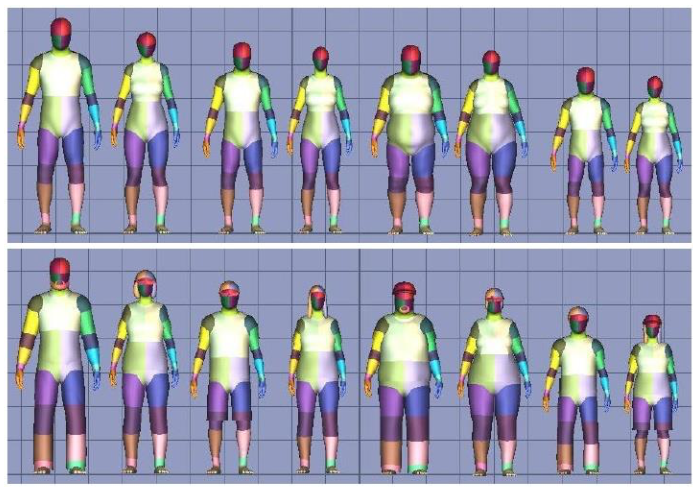
• Pixel classification results

  

Joint estimation

• Use mean shift clustering on the pixels with Gaussian kernel to infer the center of clusters.

• Clustering is done in 3d space but every pixel is weighted by their world surface area to get depth invariance.

• Finally the sum of the weighted pixels is used as a confidence measure.

• Results

  

Criticism 👎

• Not open source
• Biased towards upper body frontal poses
• Very difficult to improve or adapt.

Pose Estimation without Kinect: Convolutional Pose Machines ²

Pose Machine

• Unconstrained 2D-pose estimation on real world RGB images.

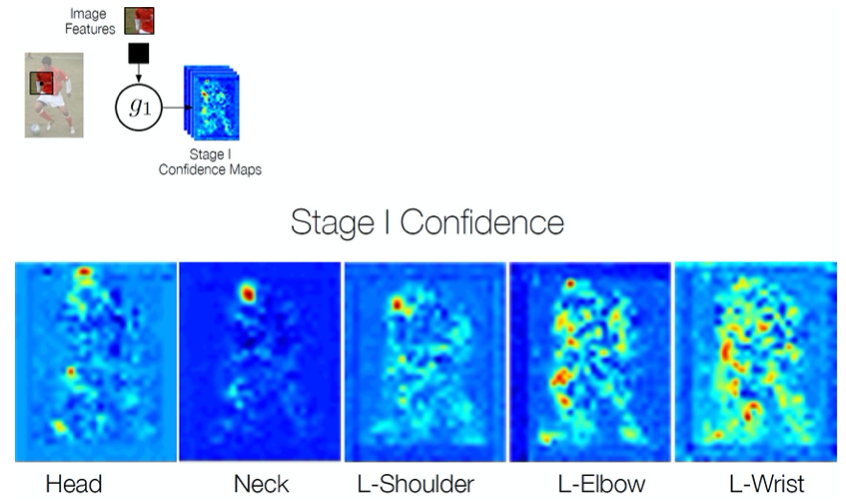
• Outputs confidence maps for every joint of the skeleton.

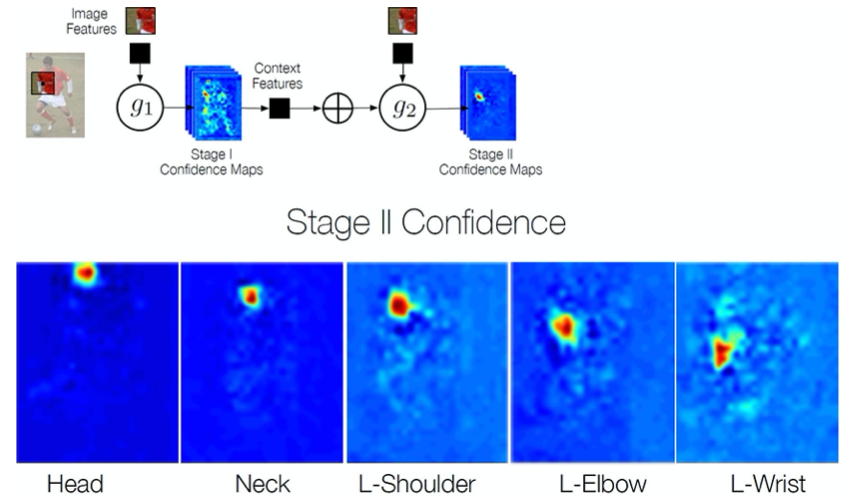
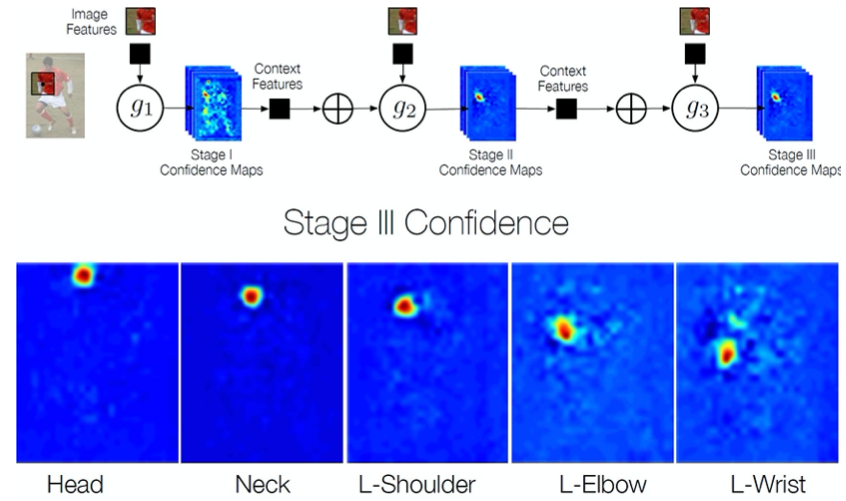
• Works in multiple stages refining the confidence maps.

• 💡 Idea:

  • Local image evidence is weak (first stage confidence maps)

  • Part context can be a strong cue (confidence maps of other body joints)

    ➔ Use confidence maps of all body joints of the previous stage to refine current results

    

Example

Details

We denote the pixel location of the $p$-th anatomical landmark (refer to as a part) $Y\_{p} \in \mathcal{Z} \subset \mathbb{R}^{2}$

• $\mathcal{Z}$: set of all $(u, v)$ locations in an image

🎯 Goal: to predict the image locations $Y = (Y\_1, \dots, Y\_P)$ for all $P$ parts.

In each stage $t \in \{1 \dots T\}$, the classifiers $g\_t$ predict beliefs for assigning a location to each part $Y\_{p}=z, \forall z \in \mathcal{Z}$, based on

• features extracted from the image at the location $z$ denoted by $\mathbf{x}\_{z} \in \mathbb{R}^{d}$ and
• contextual information from the preceding classifier in the neighborhood around each $Y\_p$ in stage $t$.

First stage

A classifier in the first stage $t = 1$ produces the following belief values:

• $b\_{1}^{p}\left(Y\_{p}=z\right)$: score predicted by the classifier $g\_1$ for assigning the $p$-th part in the first stage at image location $z$.

We represent all the beliefs of part $p$ evaluated at every location $z = (u, v)^T$ in the image as $\mathbf{b}\_{t}^{p} \in \mathbb{R}^{w \times h}$:

• $w, h$: width and height of the image, respectively

For convenience, we denote the collection of belief maps for all the parts as $\mathbf{b}\_{t} \in \mathbb{R}^{w \times h \times(P+1)}$ ($+1$ for background)

Subsequent stages

The classifier predicts a belief for assigning a location to each part $Y\_{p}=z, \forall z \in \mathcal{Z}$, based on

• features of the image data $\mathbf{x}\_{z}^{t} \in \mathbb{R}^{d}$ and
• contextual information from the preceeding classifier in the neighborhood around each $Y\_p$

• $\psi\_{t>1}(\cdot)$: mapping from the beliefs $b\_{t−1}$ to context features.

In each stage, the computed beliefs provide an increasingly refined estimate for the location of each part.

Confidence maps generation

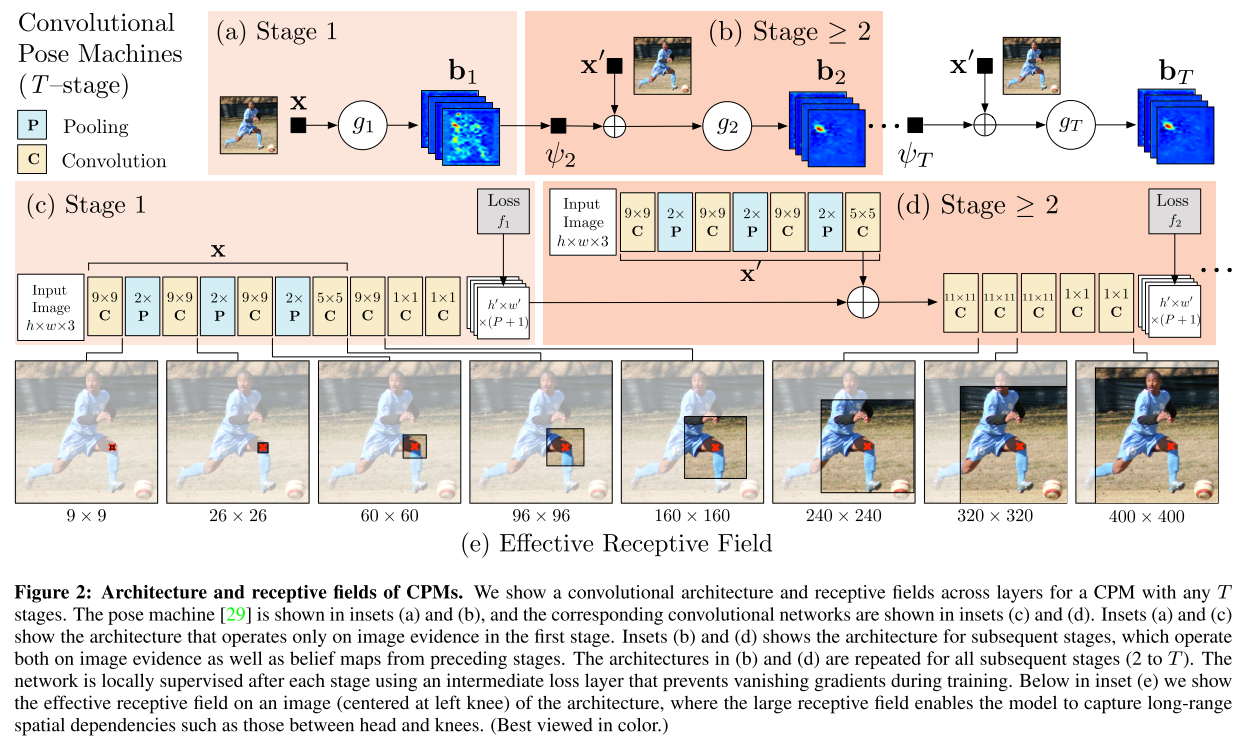
Fully Convolutional Network (FCN)

• Does not have Fully Connected Layers.
• The same network can be applied to arbitrary image sizes.
• Similar to a sliding window approach, but more efficient

CPM

The prediction and image feature computation modules of a pose machine can be replaced by a deep convolutional architecture allowing for both image and contextual feature representations to be learned directly from data.

Advantage of convolutional architectures: completely differentiale $\rightarrow$ enabling end-to-end joint trainining of all stages 👍

Learning in CPM

Potential problem of a network with a large number of layers: vanishing gradient

Solution

• Define a loss function at the output of each stage $t$ that minimizes the $l_2$ distance between the predicted ($b\_{t}^{p}$) and ideal ($b\_{*}^{p}\left(Y\_{p}=z\right)$) belief maps for each part.

  • The ideal belief map for a part $p$, $b\_{*}^{p}\left(Y\_{p}=z\right)$, are created by putting Gaussian peaks at ground truth locations of each body part $p$.

  Cost function we aim to minimize at the output of each stage at each level:

  $$f\_{t}=\sum\_{p=1}^{P+1} \sum\_{z \in \mathcal{Z}}\left\|b\_{t}^{p}(z)-b\_{*}^{p}(z)\right\|\_{2}^{2} .$$
  • $P$: all body parts
  • $\mathcal{Z}$: set of all image locations in a believe map

• The overall objective for the full architecture is obtained by adding the losses at each stage:

  $$\mathcal{F}=\sum\_{t=1}^{T} f\_{t}$$