Gesture Recognition

Introduction

Gesture

• a movement usually of the body or limbs that expresses or emphasizes an idea, sentiment, or attitude
• the use of motions of the limbs or body as a means of expression

Automatic Gesture Recognition

• A gesture recognition system generates a semantic description for certain body motions
• Gesture recognition exploits the power of non-verbal communication, which is very common in human-human interaction
• Gesture recognition is often built on top of a human motion tracker

Applications

• Multimodal Interaction
  • Gestures + Speech recognition
  • Gestures + gaze
  • Human-Robot Interaction
  • Interaction with Smart Environments
• Understanding Human Interaction

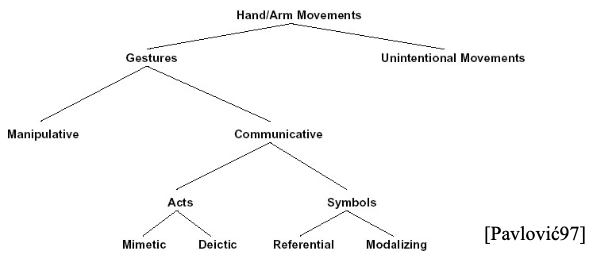
Types of Gestures

• Hand & arm gestures

  • Pointing Gestures
  • Sign Language

• Head gestures

  • Nodding, head shaking, turning, pointing

• Body gestures

Automatic Gesture Recognition

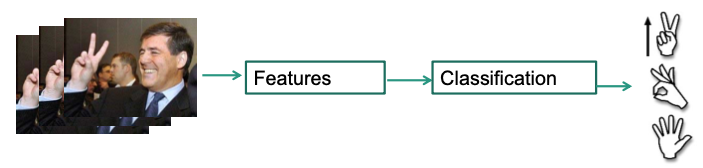
• Feature Acquisition
  • Appearances: Markers, color, motion, shape, segementation, stereo, local descriptors, space-time interest points, …
  • Model based: body- or hand-models
• Classifiers
  • SVM, ANN, HMMs, Adaboost, Dec. Trees, Deep Learning …

Hidden Markov Models (HMMs) for Gesture Recognition

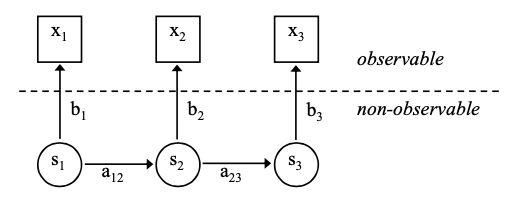
• “hidden”: comes from observing observations and drawing conclusions WITHOUT knowing the hidden sequence of states

• Markov assumption (1st order): the next state depends ONLY on the current state (not on the complete state history)

A Hidden Markov Model is a five-tuple

• $S = \\{s\_1, s\_2, \dots, s\_n\\}$: set of states
• $\pi$: the initial probability distribution
  • $\pi(s\_i)$ = probability of $s\_i$ being the first state of a state sequence
• $\mathbf{A} = (a\_{ij})$: the matrix of state transition probabilities
  • $(a\_{ij})$: probability of state $s\_j$ following $s\_i$
• $B = \\{b\_1, b\_2, \dots, b\_n\\}$: the set of emission probability distributions/densities
  • $b\_i(x)$: probability of observing $x$ when the system is in state $s\_i$
• $V$: the observable feature space
  • Can be discrete ($V = \\{x\_1, x\_2, \dots, x\_v\\}$) or continuous ($V = \mathbb{R}^d$)

Properties of HMMs

• For the initial probabilities:

  $$\sum\_i \pi(s\_i) = 1$$
  • Often simplified by $$\pi(s\_1) = 1, \quad \pi(s\_i > 1) = 0$$

• For state transition probabilities:

  $$\forall i: \sum\_j a\_{ij} = 1$$
  • Often: $a\_{ij} = 0$ for most $j$ except for a few states

• When $V = \\{x\_1, x\_2, \dots, x\_v\\}$ then $b\_i$ are discrete probability distributions, the HMMs are called discrete HMMs

• When $V = \mathbb{R}^d$ then $b\_i$ are continuous probability density functions, the HMMs are called continuous (density) HMMs

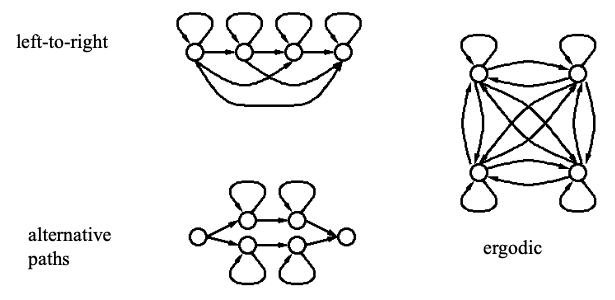
HMM Topologies

The Observation Model

Most popular: Gaussian mixture models

• $n\_j$: number of Gaussians (in state $j$)
• $c\_{jk}$: mixture weight for $k$-th Gaussian (in state $j$)
• $\mu\_{jk}$: means of $k$-th Gaussian (in state $j$)
• $\Sigma\_{jk}$: covariane matrix of $k$-th Gaussian (in state $j$)

Three Main Tasks with HMMs

Given an HMM $\lambda$ and an observation $x\_1, x\_2, \dots, x\_T$

• The evaluation problem

  compute the probability of the observation $p(x\_1, x\_2, \dots, x\_T | \lambda)$

  $\rightarrow$ “Forward Algorithm”

• The decoding problem

  compute the most likely state sequence $s\_{q1}, s\_{q2}, \dots, s\_{qT}$, i.e.

  $$\operatorname{argmax}\_{q 1, \ldots, q \tau} p\left(q\_{1}, . ., q\_{T} \mid x\_{1}, x\_{2}, \ldots, x\_{T}, \lambda\right)$$

  $\rightarrow$ “Viterbi-Algorithm”

• The learning/optimization problem

  Find an HMM $\lambda^\prime$ s.t. $p\left(x\_{1}, x\_{2}, \ldots, x\_{T} \mid \lambda^{\prime}\right)>p\left(x\_{1}, x\_{2}, \ldots, x\_{T} \mid \lambda\right)$

  $\rightarrow$ “Baum-Welch-Algo”, “Viterbi-Learning”

Sign Language Recognition

• American Sign Language (ASL)
  • 6000 gesture describe persons, places and things
  • Exact meaning and strong rules of context and grammar for each
• Sign recognition
  • HMM ideal for complex and structured hand gestures of ASL

Feature extraction

• Camera either located as a 1st-person and a 2nd-person view
• Segment hand blobs by a skin color model

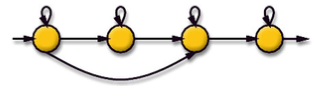
HMM for American Sign Language

• Four-State HMM for each word

  

• Training

  • Automatic segmentation of sentences in five portions
  • Initial estimates by iterative Viterbi-alignment
  • Then Baum-Welch re-estimation
  • No context used

• Recognition

  • With and without part-of-speech grammar
  • All features / only relative features used

ASL Results

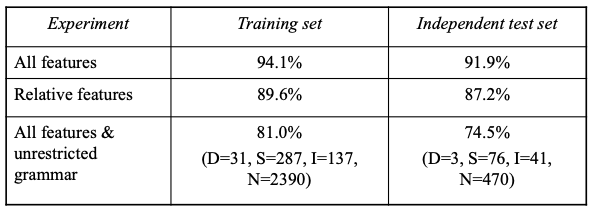
Desk-based

348 training and 94 testing sentences without contexts

Accuracy:

• $N$: #Words
• $D$: #Deletions
• $S$: #Substituitions
• $I$: #Insertions

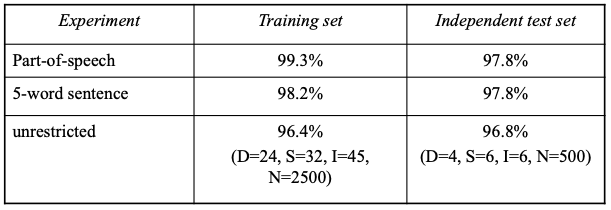
Wearable-based

• 400 training sentences and 100 for testing
• Test 5-word sentences
• Restricted and unrestricted similar!

Pointing Gesture Recognition

• Pointing gestures

  • are used to specify objects and locations

  • can be needful to resolve ambiguities in verbal statements

• Definition: Pointing gesture = movement of the arm towards a pointing target

• Tasks

  • Detect occurrence of human pointing gestures in natural arm movements
  • Extract the 3D pointing direction

Interaction in a Smart Room