👍 Batch Normalization
TL;DR
Problem: During training, updating a lower layer changes the input distribution for the next layer → next layer constantly needs to adapt to changing inputs
💡Idea: mean/variance normalization step between layers
Faster / more effective training
Gradients less dependent on scale of parameters
Allow higher learning rates
Combat saturation problem
How:
Mean over the batch dimension
Variance of the mini-batch
Normalization
Scale and shift ( and are network parameters)
Motivation: Feature scaling
Make different features have the same scaling (normalizing the data)
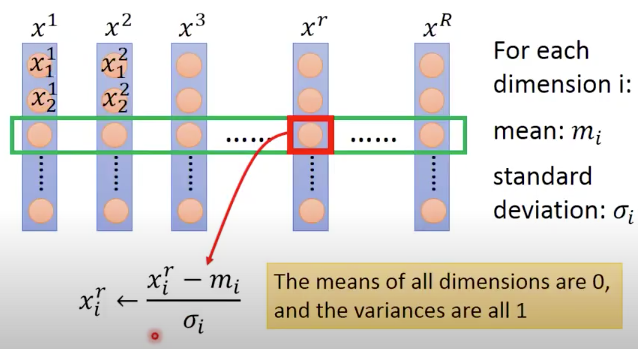
- : the -th feature of the -th input sample/instance
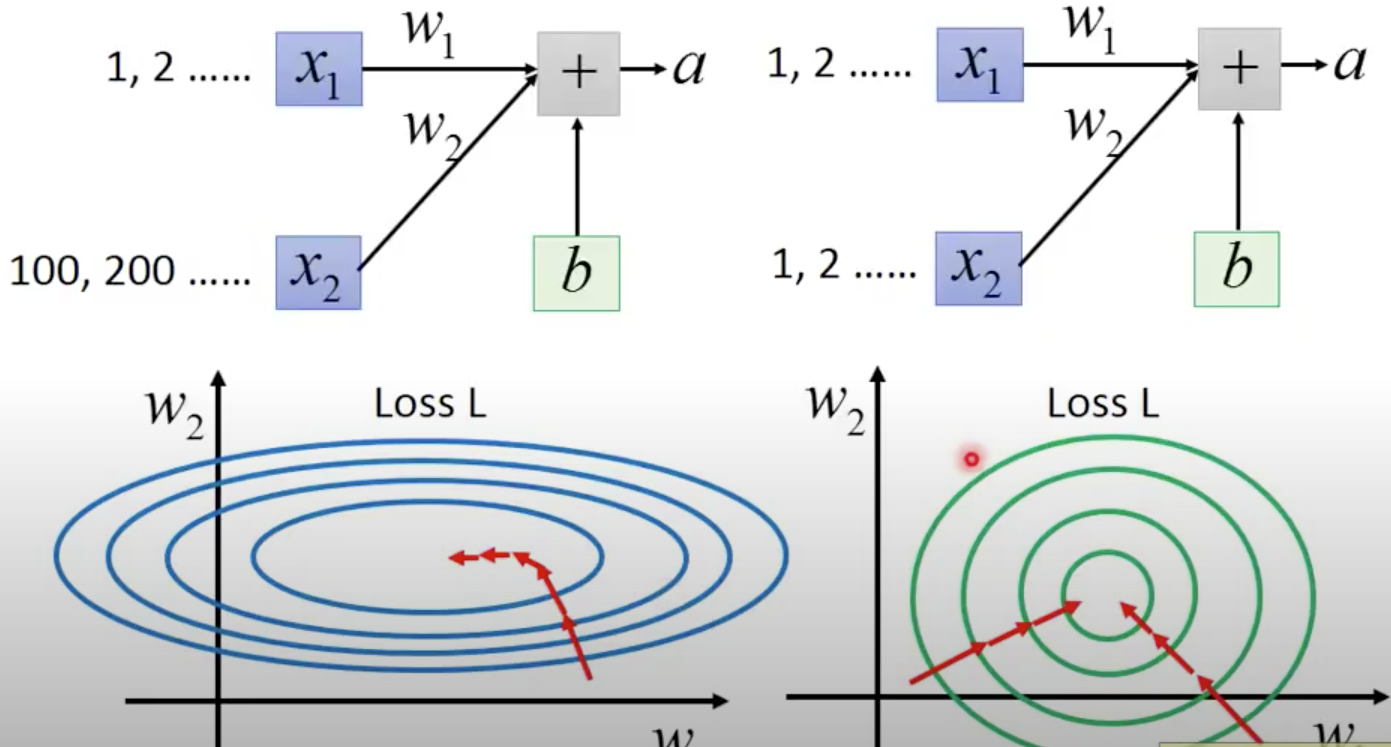
In general, gradient descent converges much faster with feature scaling than without it.
Illustration:
In hidden layer
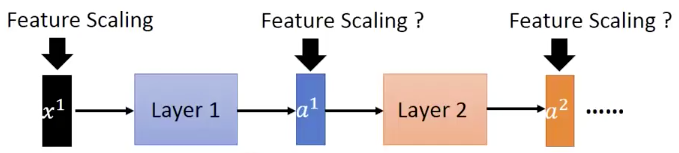
From the point of view of Layer 2, its input is , which is the output of Layer 1. As feature scaling helps a lot in training (gradient descent will converge much faster), can we also apply feature scaling for and the other hidden layer’s output (such as )?
Internal Covariate Shift
In Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift, the author’s definition is:
We define Internal Covariate Shift as the change in the distribution of network activations due to the change in network parameters during training.
In neural networks, the output of the first layer feeds into the second layer, the output of the second layer feeds into the third, and so on. When the parameters of a layer change, so does the distribution of inputs to subsequent layers.
These shifts in input distributions can be problematic for neural networks, especially deep neural networks that could have a large number of layers.
A common solution is to use small learning rate, but the training would then be slower. 😢
Batch Nomalization (BN)
💪 Aim: solve internal covariate shift
Batch
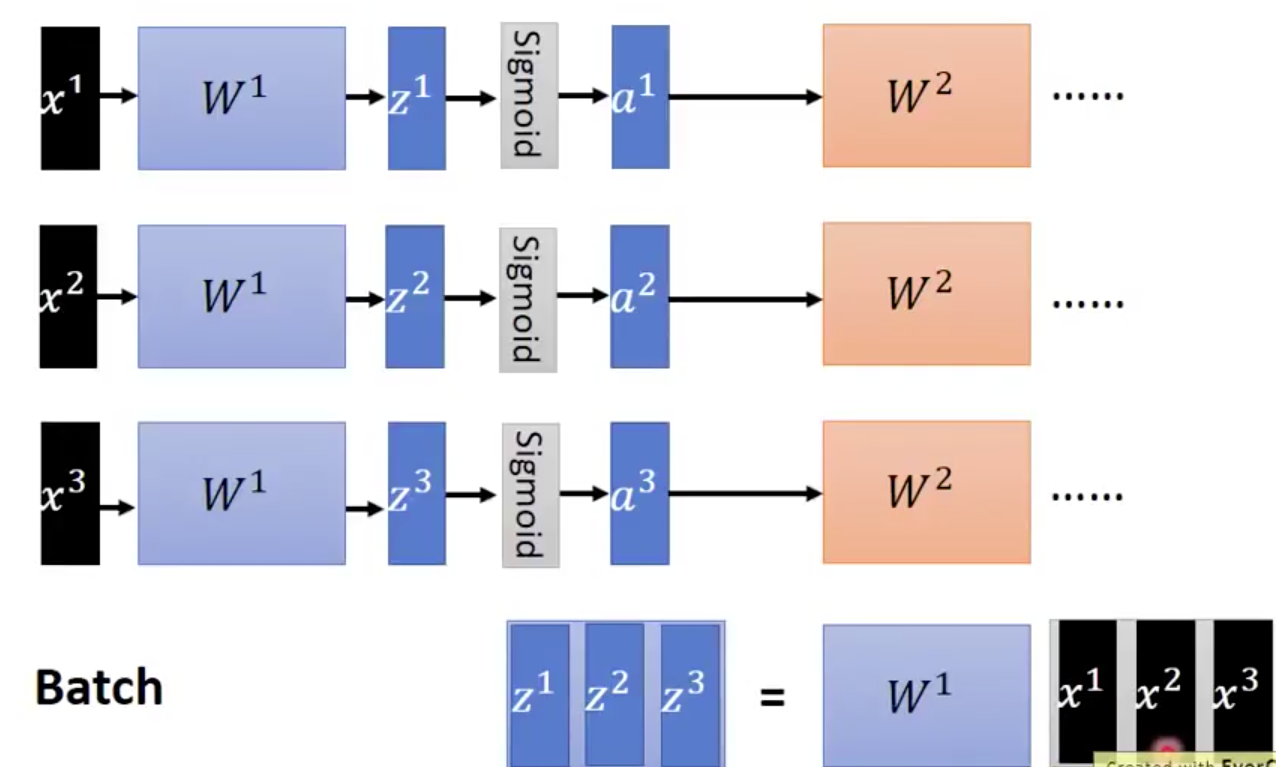
Batch normalization
Usually we apply BN on the input of the activation function (i.e., before activation function )
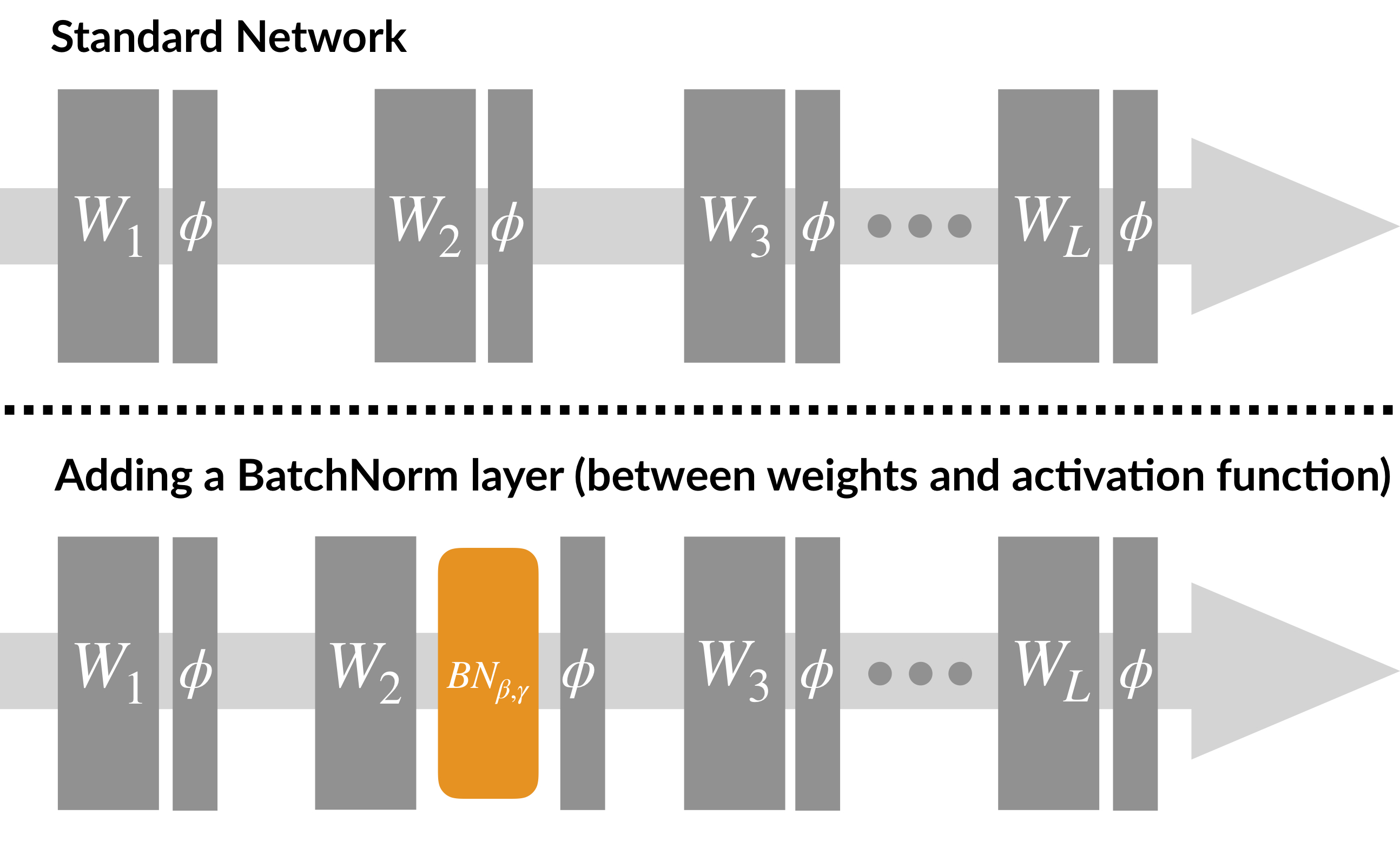
Take the first hidden layer as example:
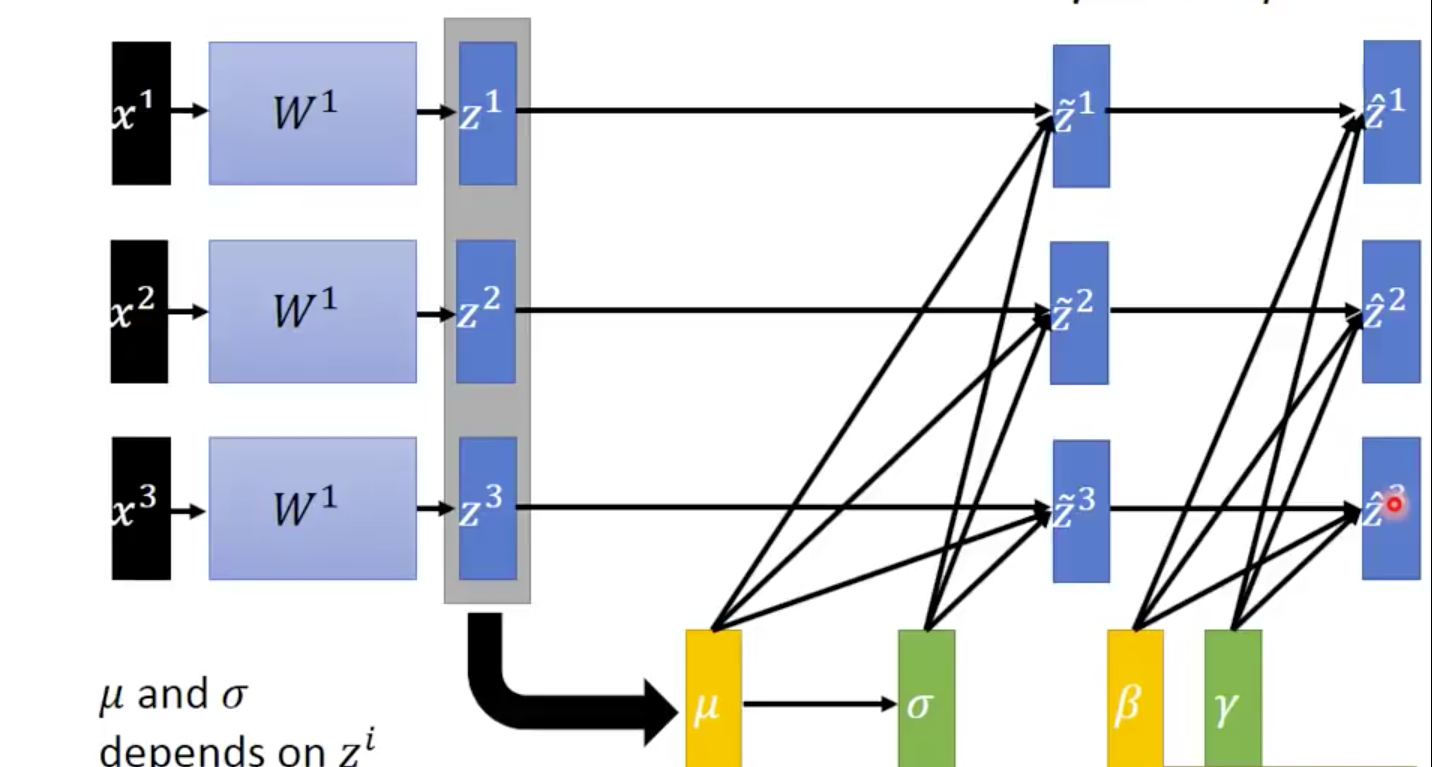
- Compute mean
- Compute standard deviation
Normalize (Division is element-wise)
Now has zero mean and unit variance.
- Good for activation function which could saturate (such as sigmoid, tanh, etc.)
Sigmoid witout BN Sigmoid with BN 
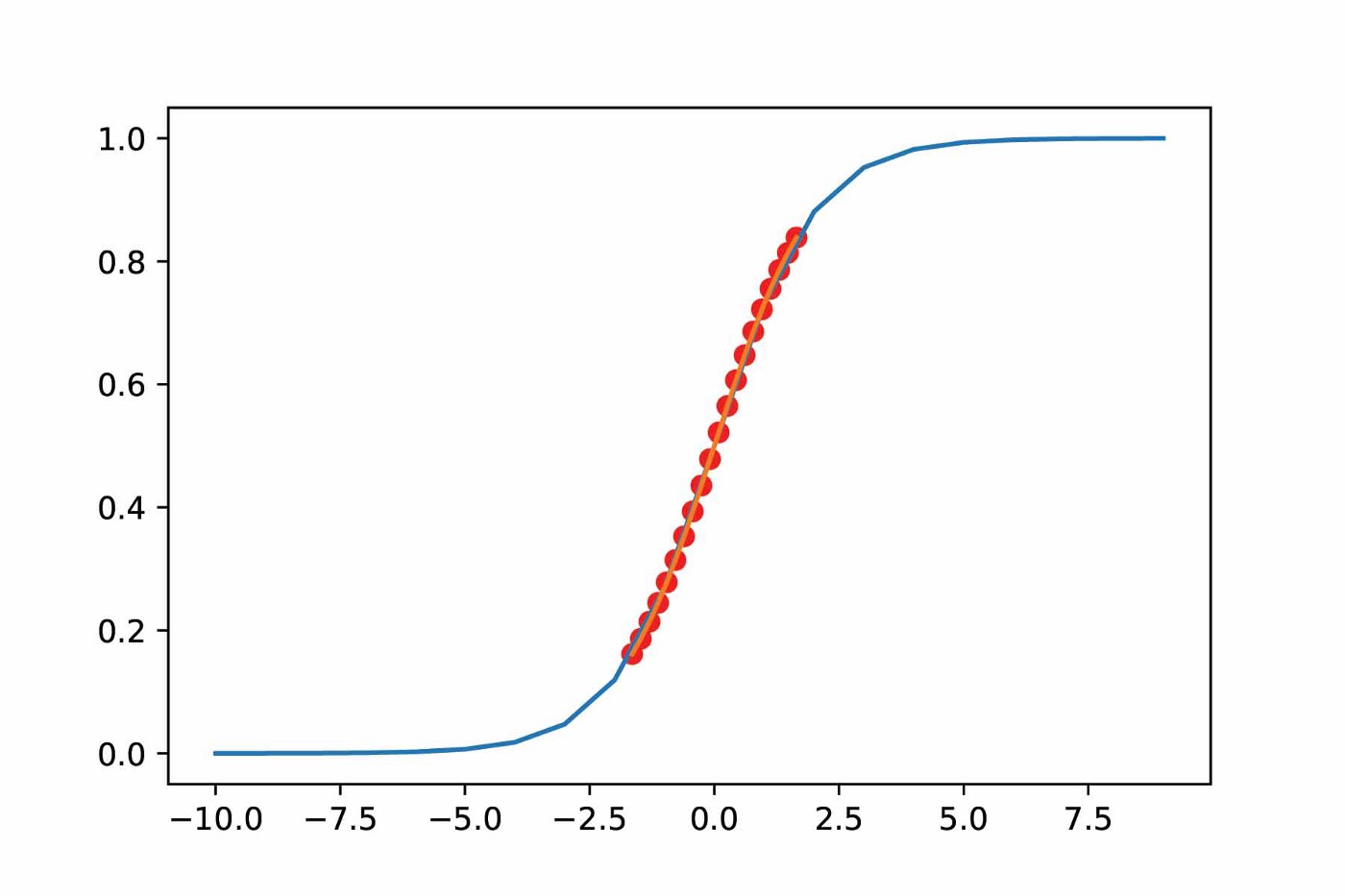
- Good for activation function which could saturate (such as sigmoid, tanh, etc.)
Scale and shift
- In practice, restricting the activations of each layer to be strictly zero mean and unit variance can limit the expressive power of the network.
- E,g,, some activation function doesn’t require the input to be zero mean and unit variance
- Scaling and shifting allow the network to learn input-independent parameters and that can convert the mean and variance to any value that the network desires
- In practice, restricting the activations of each layer to be strictly zero mean and unit variance can limit the expressive power of the network.
Note:
Ideally, and should be computed using the whole training dataset
But this is expensive and infeasible
- The size of training dataset is enormous
- When gets updated, the output of the hidden layer will change, we have to compute and again
In practice, we can apply BN on batch of data, instead of the whole training dataset
But the size of bach can not be too small
If we apply BN on a small batch, it is difficult to estimate the mean () and the standard deviation () of the WHOLE training dataset
The performance of BN will be bad!
BN in Testing

Problem: We do NOT have batch at testing stage. How can we estimate and ?
Ideal solution: Compute and using the whole training set
- But it is difficult in pratice
- Traing set too large
- Training could be online training
Practical solution: Compute the moving average of and of the batches during training
👍 Benefit of BN
Reduce training times, and make very deep net trainable
- Less covariate shift, we can use larger learning rate
- less exploding/vanishing gradients
- Especailly effective for sigmoid, tanh, etc.
Learning is less affected by parameters initialization

Reduces the demand for regularization, helps preventing overfitting
Layer Normalization
Batch Normalization was wonderful, but not always applicable
When large mini-batch was not feasible
It was difficult to apply for Recurrent Neural Networks
Alternative: Layer Normalization
Perform
over the feature dimension
Not as effective as Batch Normalization, but still widely used because of better efficiency.
Normalization Techniques Comparison
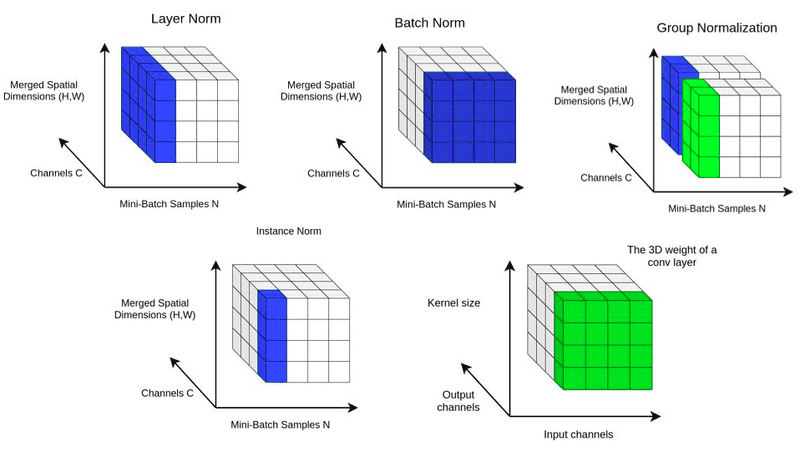
Normalization techniques. (Source: In-layer normalization techniques for training very deep neural networks)