👍 Transformer
TL;DR
Transformer
High-Level Look
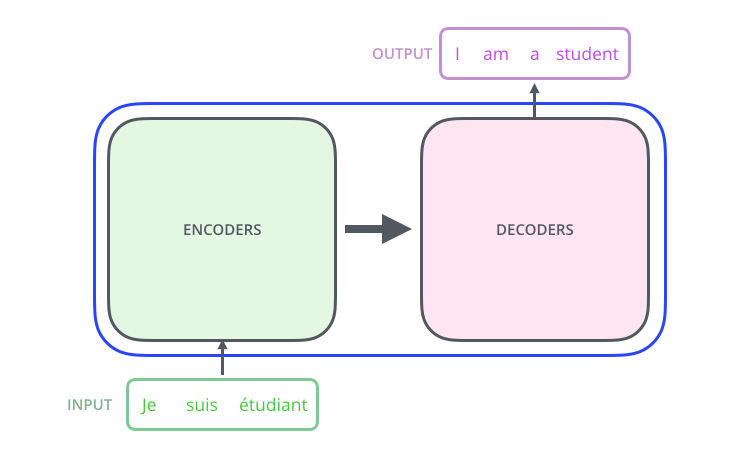
Let’s begin by looking at the model as a single black box. In a machine translation application, it would take a sentence in one language, and output its translation in another.

The transformer consists of
- an encoding component
- a decoding component
- connections between them
Let’s take a deeper look:
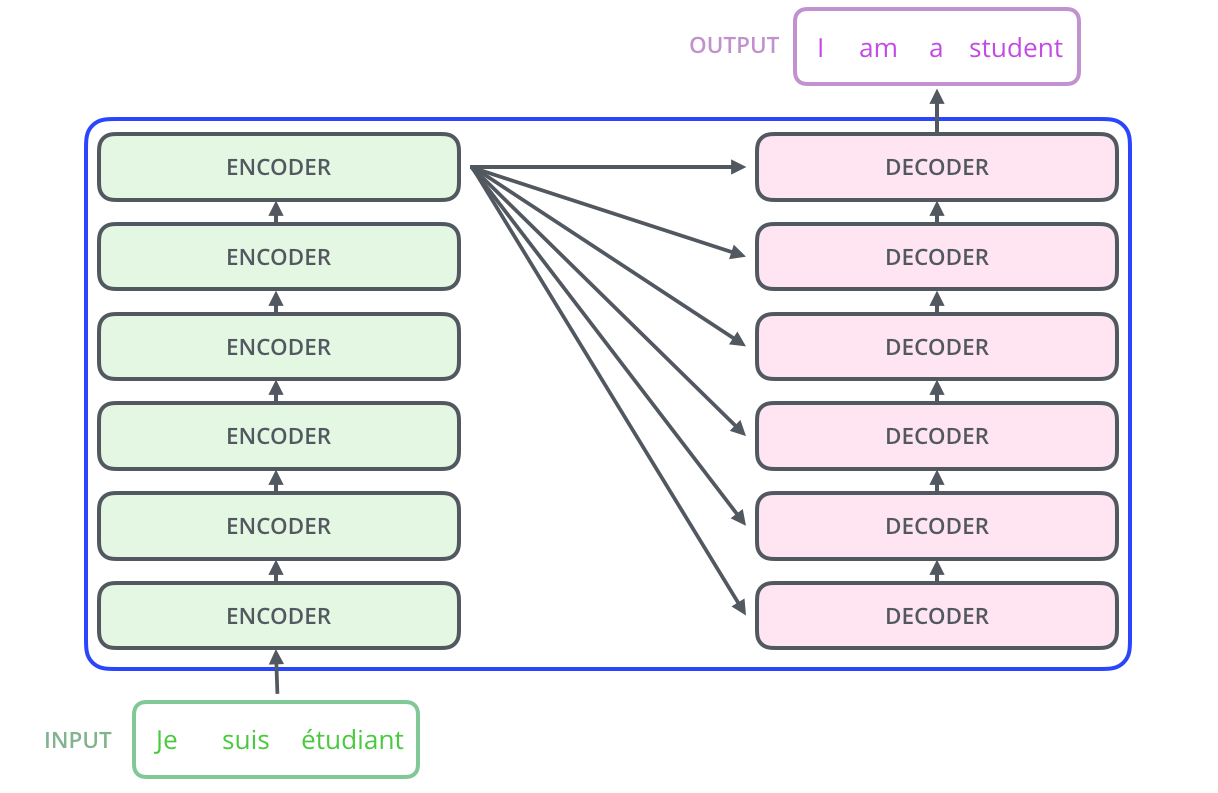
The encoding component is a stack of encoders (the paper stacks six of them on top of each other – there’s nothing magical about the number six, one can definitely experiment with other arrangements).
The decoding component is a stack of decoders of the same number.
Encoder
The encoders are all identical in structure (yet they do NOT share weights). Each one is composed of two sub-layers:
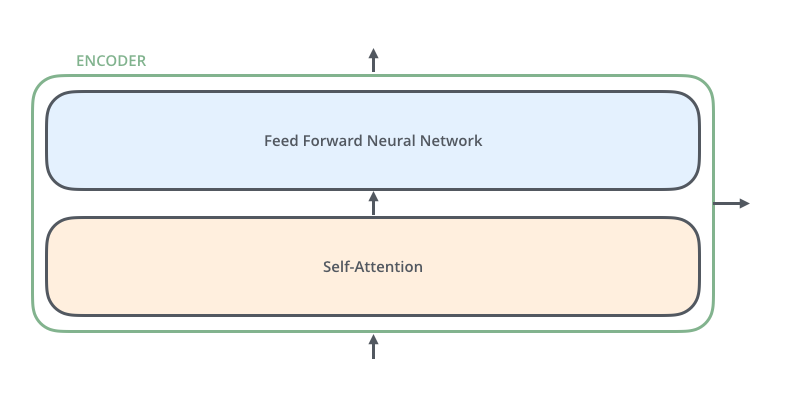
- Self-attention layer: helps the encoder to look at other words in the input sentence as it encodes a specific word.
- Feed Forwrd Neural Network (FFNN): The exact same feed-forward network is independently applied to each position.
Decoder
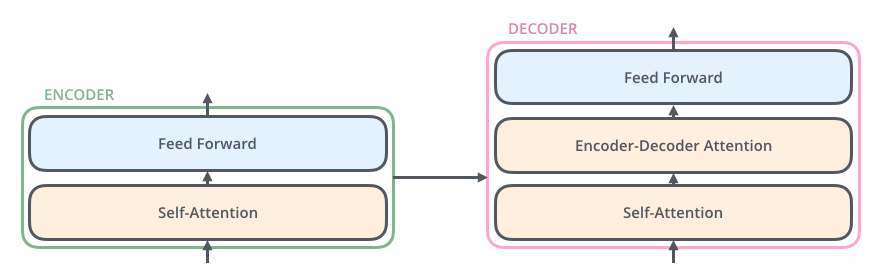
The decoder has both those layers, but between them is an attention layer that helps the decoder focus on relevant parts of the input sentence (similar what attention does in seq2seq models)
Encoding Component
How tensors/vectors flow
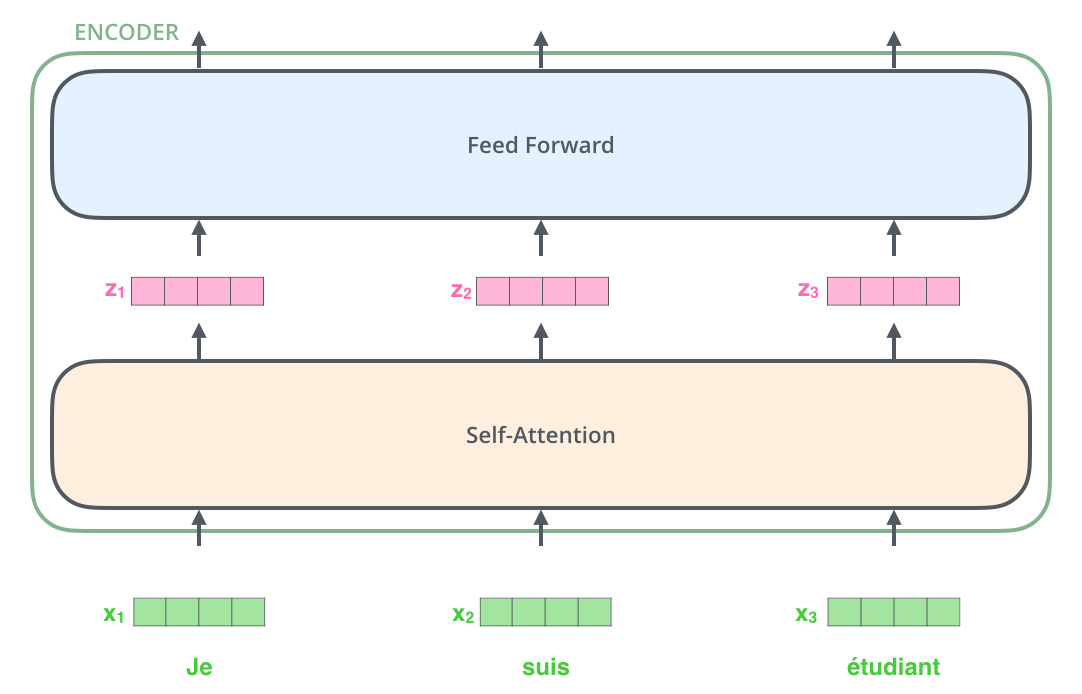
As is the case in NLP applications in general, we begin by turning each input word into a vector using an embedding algorithm.

Each word is embedded into a vector of size 512. We’ll represent those vectors with these simple boxes.
Note that the embedding ONLY happens in the bottom-most encoder.
The abstraction that is common to all the encoders is that they receive a list of vectors each of the size 512 (The size of this list is hyperparameter we can set – basically it would be the length of the longest sentence in our training dataset.)
- In bottom encoder: word embeddings
- In other encoders: output of the encoder that’s directly below
After embedding the words in our input sequence, each of them flows through each of the two layers of the encoder.
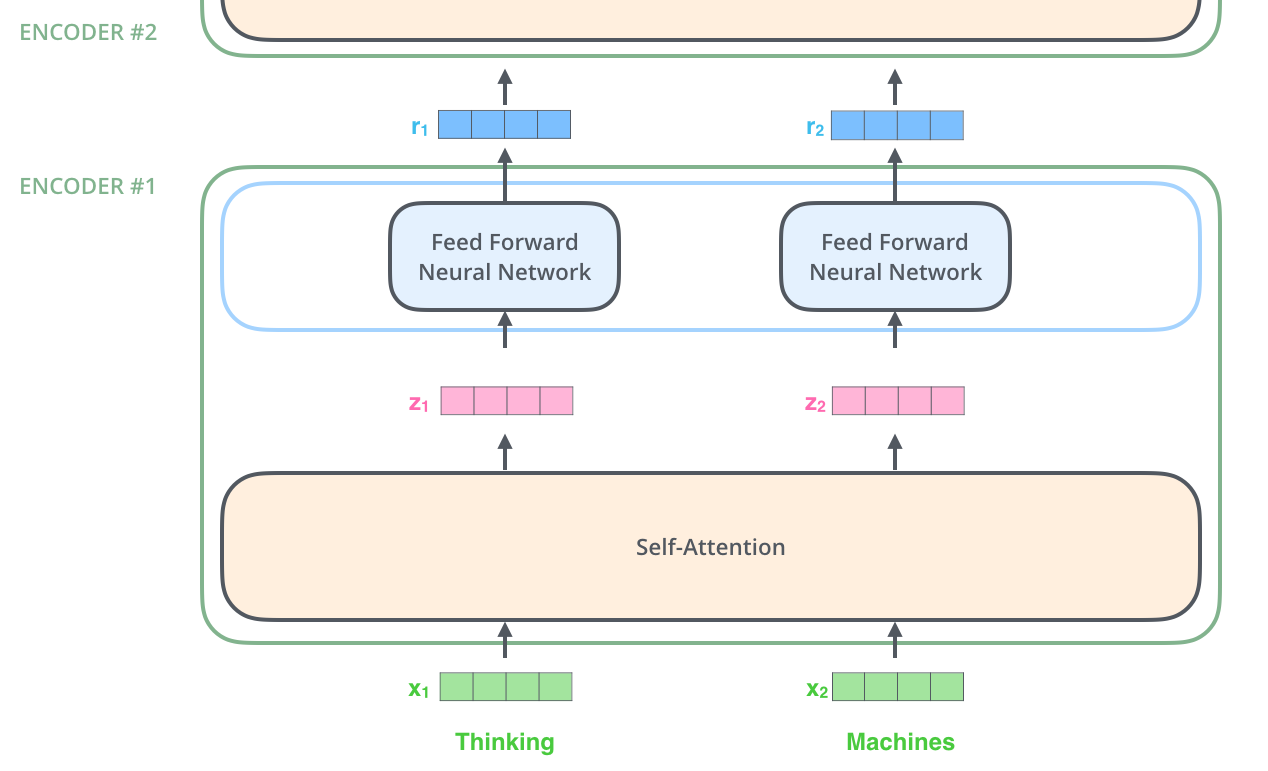
- The word in each position flows through its own path in the encoder. There are dependencies between these paths in the self-attention layer.
- The feed-forward layer does not have those dependencies, thus the various paths can be executed in parallel while flowing through the feed-forward layer. 👏
In summary, An encoder
- receives a list of vectors as input
- processes this list by passing these vectors into a ‘self-attention’ layer, then into a feed-forward neural network
- sends out the output upwards to the next encoder.
Self-Attention
Say the following sentence is an input sentence we want to translate:
”The animal didn't cross the street because it was too tired”
What does “it” in this sentence refer to? Is it referring to the street or to the animal? It’s a simple question to a human, but not as simple to an algorithm.
As the model processes each word (each position in the input sequence), self attention allows it to look at other positions in the input sequence for clues that can help lead to a better encoding for this word. Therefore, when the model is processing the word “it”, self-attention allows it to associate “it” with “animal”.
We can think of how maintaining a hidden state allows an RNN to incorporate its representation of previous words/vectors it has processed with the current one it’s processing. Self-attention is the method the Transformer uses to bake the “understanding” of other relevant words into the one we’re currently processing.

When encoding the word ‘it’ in 5.encoder (the top encoder in the stack), part of the attention mechanism was focusing on ‘The Animal’, and baked a part of its representation into the encoding of ‘it’. (Visualization source: Tensor2Tensor notebook)
Self-Attention in Detail
Calculate self-attention using vectors:
Create three vectors
- Query vector
- Key vector
- Value vector
from each of the encoder’s input vectors by multiplying the embedding by three matrices that we trained during the training process.
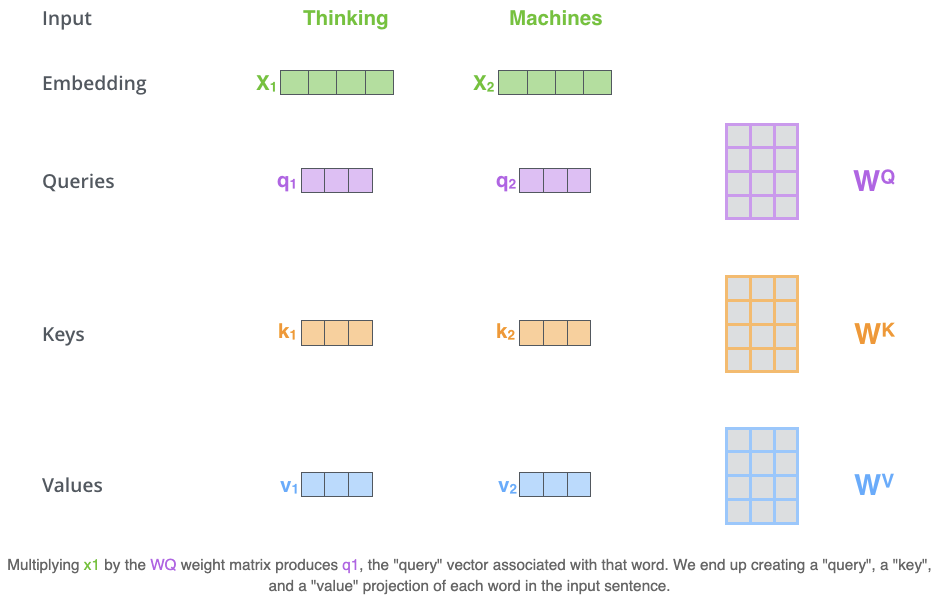
These new vectors are smaller in dimension (64) than the embedding vector (512). They don’t have to be smaller, this is an architecture choice to make the computation of multiheaded attention (mostly) constant.
calculate a score
The score determines how much focus to place on other parts of the input sentence as we encode a word at a certain position.
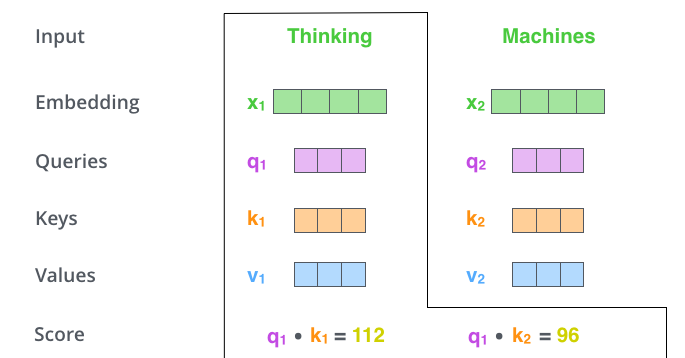
- Say we’re calculating the self-attention for the first word in this example, “Thinking”. We need to score each word of the input sentence against this word.
The score is calculated by taking the dot product of the query vector with the key vector of the respective word we’re scoring.
- So if we’re processing the self-attention for the word in position #1, the first score would be the dot product of q1 and k1. The second score would be the dot product of q1 and k2.
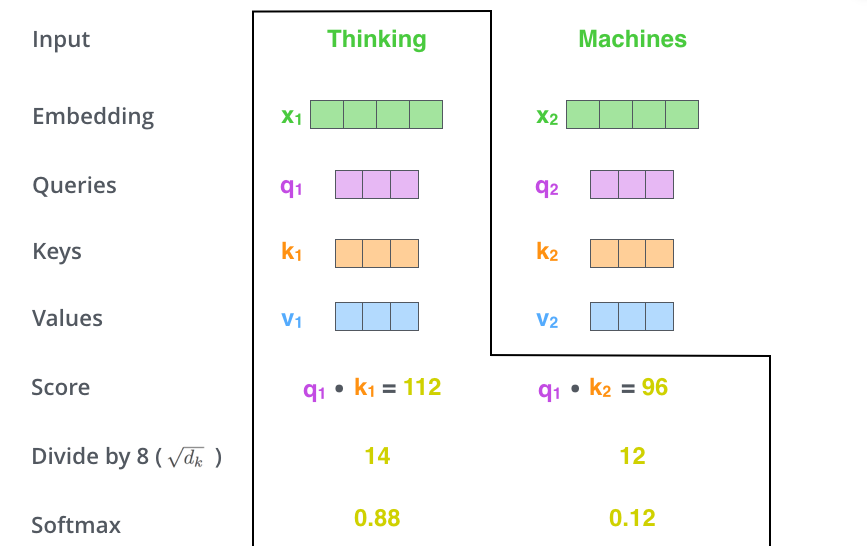
Divide the scores by the square root of the dimension of the key vectors
In paper the dimension of the key vectors is 64. Therefore devide the scores by 8
(There could be other possible values here, but this is the default)
This leads to having more stable gradients. 👏
Pass the result through a softmax operation
- Softmax normalizes the scores so they’re all positive and add up to 1.
- The softmax score determines how much each word will be expressed at this position.
- Clearly the word at this position will have the highest softmax score
- but sometimes it’s useful to attend to another word that is relevant to the current word.
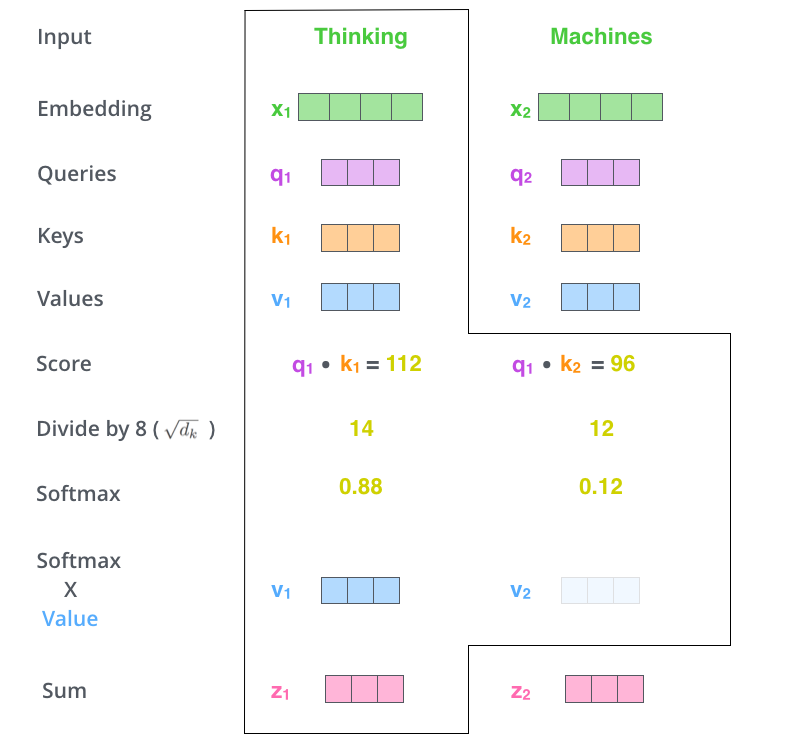
Multiply each value vector by the softmax score (in preparation to sum them up)
- Keep intact the values of the word(s) we want to focus on
- drown-out irrelevant words (by multiplying them by tiny numbers like 0.001, for example)
Sum up the weighted value vectors
- This produces the output of the self-attention layer at this position (for the first word).
- The resulting vector is one we can send along to the feed-forward neural network.
Matrix Calculation of Self-Attention
In the actual implementation, the above calculation is done in matrix form for faster processing.
Calculate the Query, Key, and Value matrices
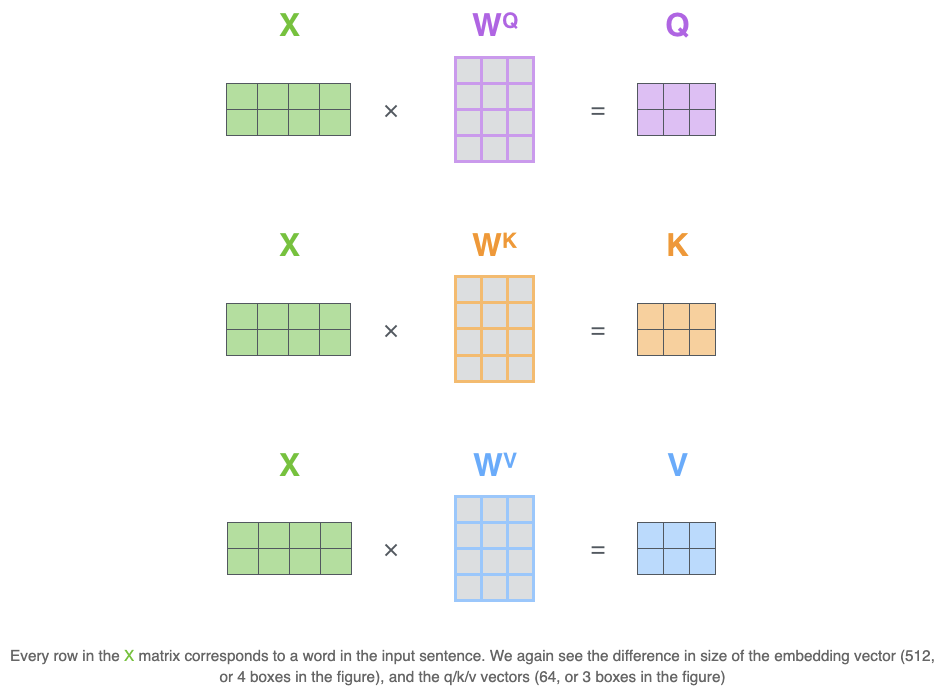
- Pack our embeddings into a matrix X
- Multiplying it by the weight matrices we’ve trained (, , )
Calculate the outputs of the self-attention layer
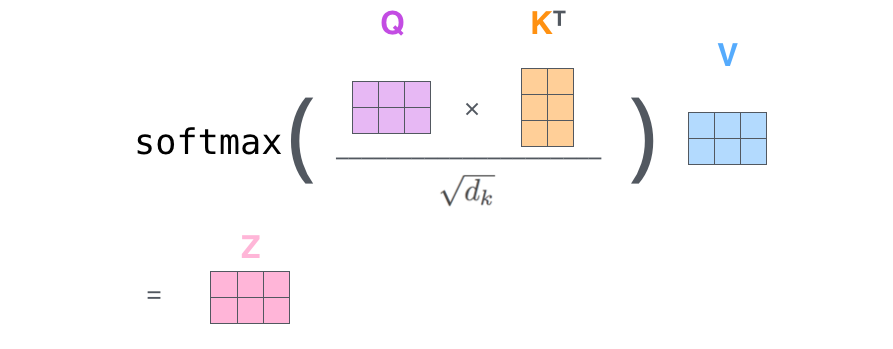
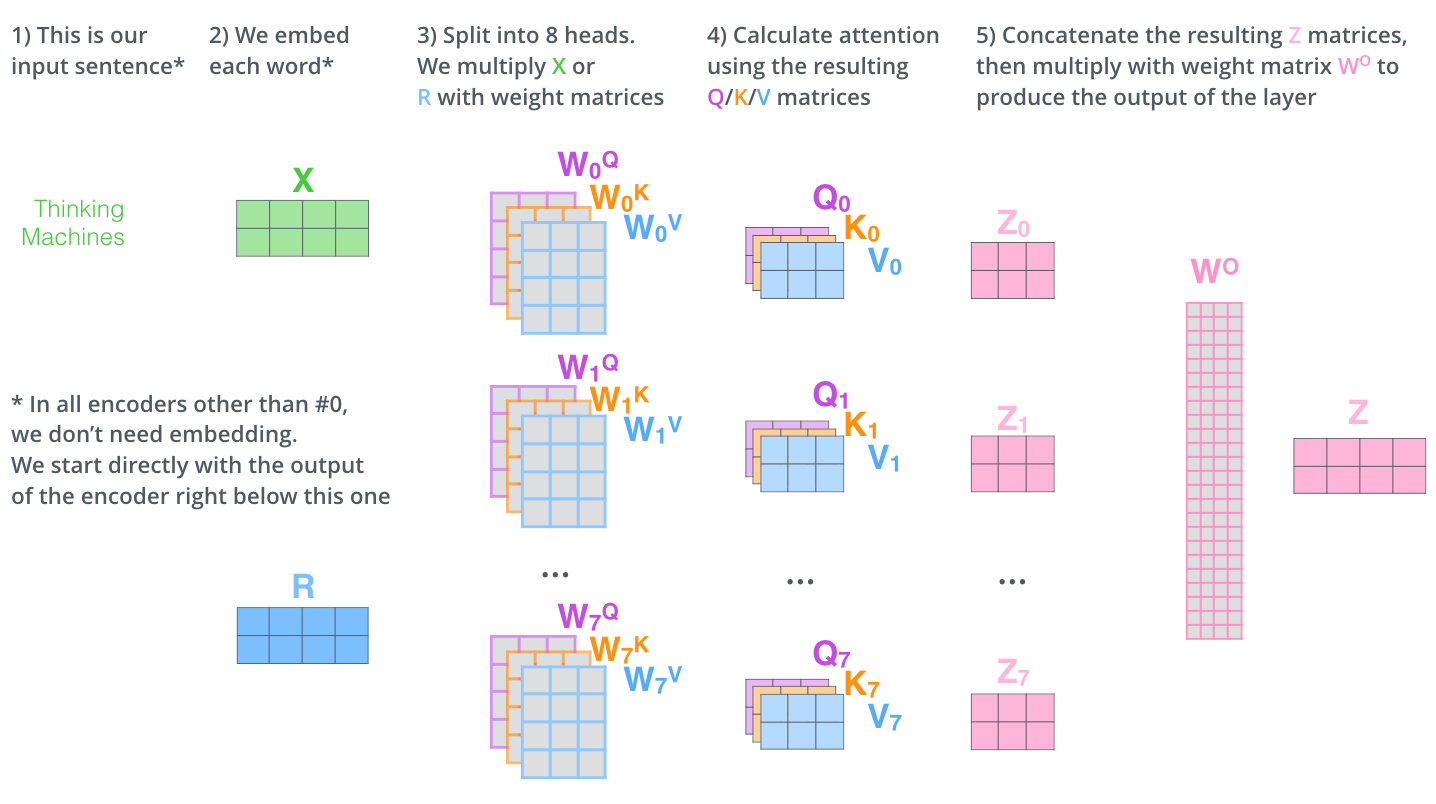
“Multi-headed” Mechanism
The paper further refined the self-attention layer by adding a mechanism called “multi-headed” attention. This improves the performance of the attention layer in two ways:
Expands the model’s ability to focus on different positions
Gives the attention layer multiple “representation subspaces”
With multi-headed attention we have not only one, but multiple sets of Query/Key/Value weight matrices
(the Transformer uses eight attention heads, so we end up with eight sets for each encoder/decoder)
Each of these sets is randomly initialized.
After training, each set is used to project the input embeddings (or vectors from lower encoders/decoders) into a different representation subspace.
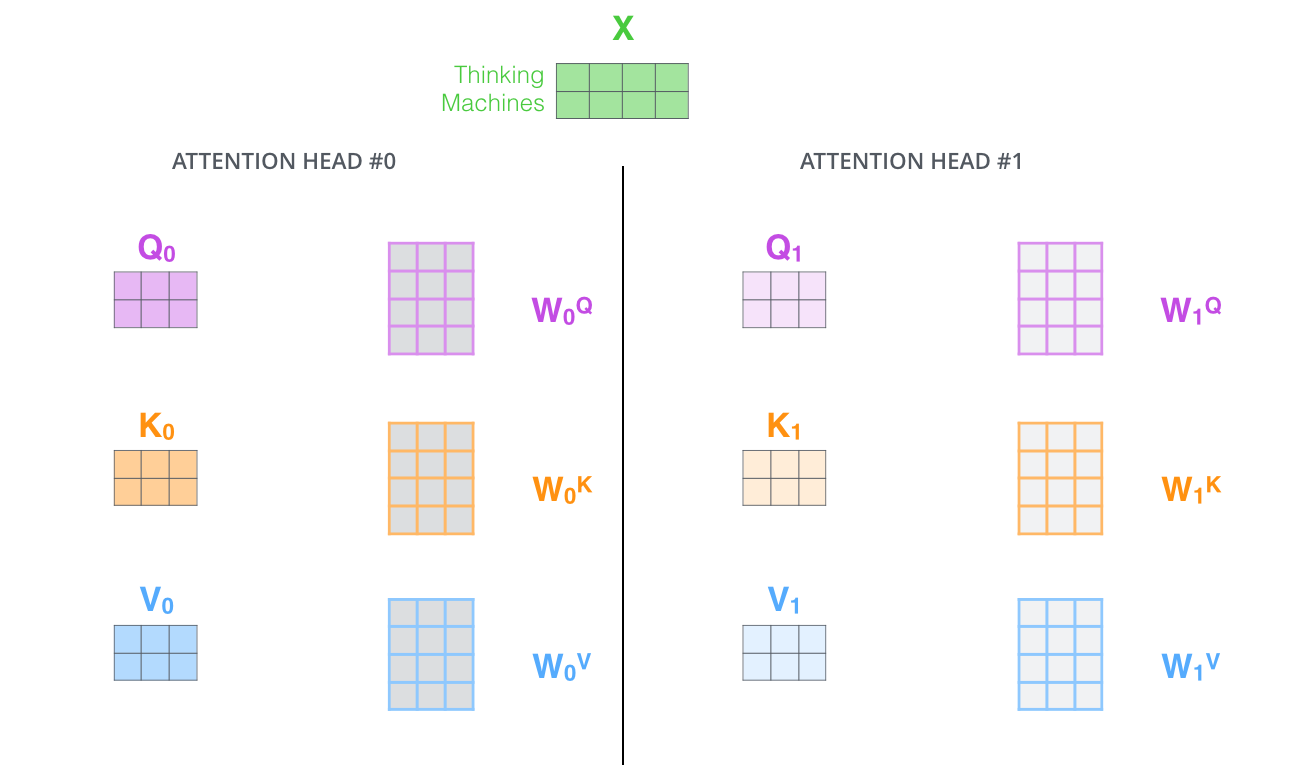
With multi-headed attention, we maintain separate // weight matrices for each head resulting in different // matrices. As we did before, we multiply by the // matrices to produce // matrices.
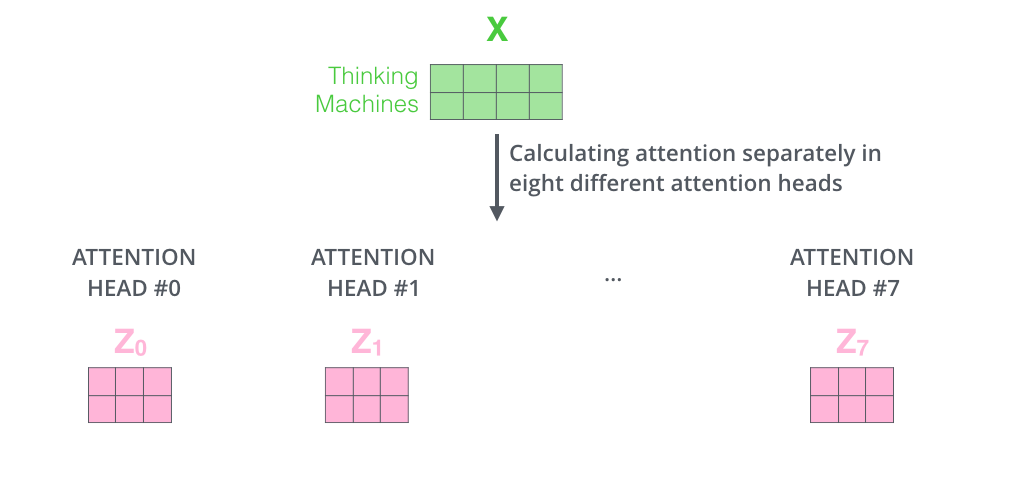
If we do the same self-attention calculation as above, just eight different times with different weight matrices, we end up with eight different matrices
Since the feed-forward layer is expecting a single matrix (a vector for each word), we concat the matrices then multiple them by an additional weights matrix .
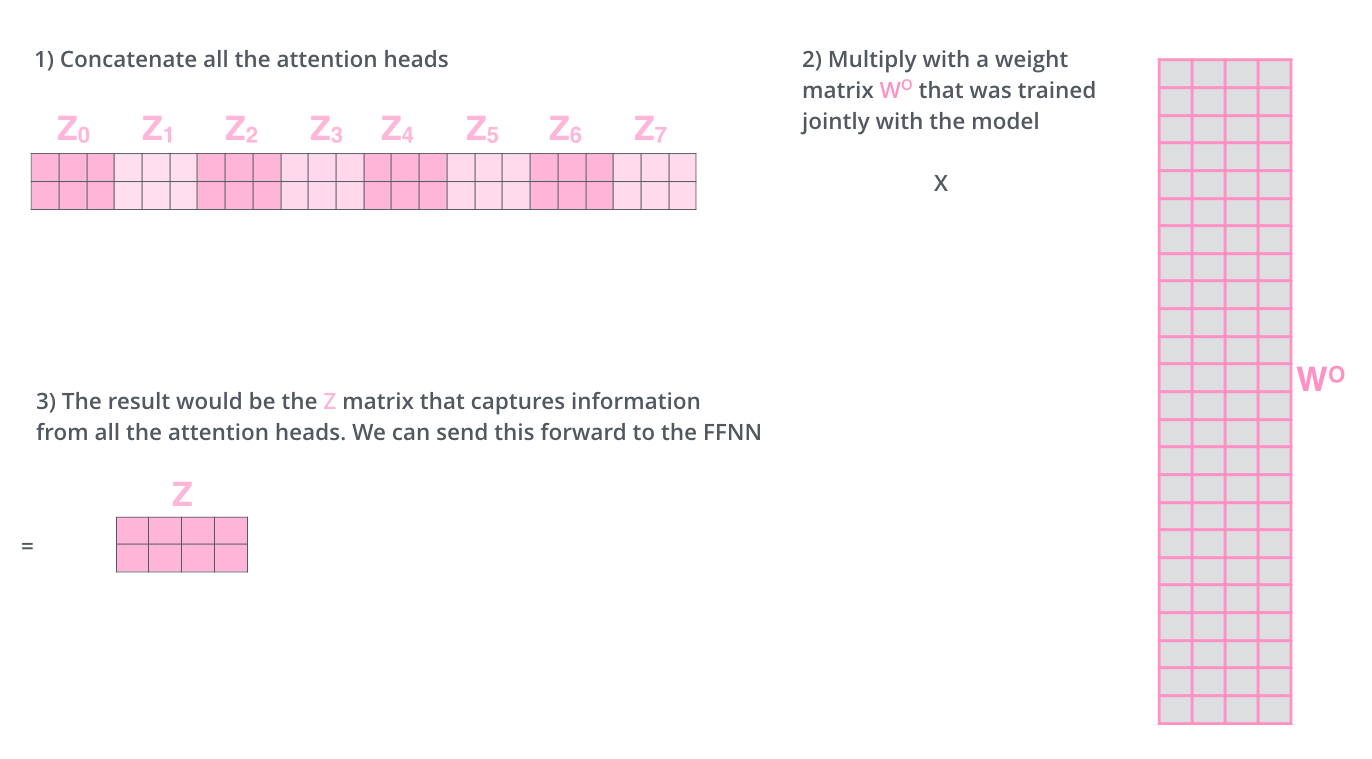
Summarize them into a figure
Example
Let’s revisit our example from before to see where the different attention heads are focusing as we encode the word “it” in our example sentence:

As we encode the word ‘it’, one attention head is focusing most on ’the animal’, while another is focusing on ’tired’ – in a sense, the model’s representation of the word ‘it’ bakes in some of the representation of both ‘animal’ and ’tired’. (Visualization source: Tensor2Tensor notebook)
Representing The Order of The Sequence Using Positional Encoding
In order to represent the order of the words in the input sequence, the transformer adds a vector to each input embedding.
- These vectors follow a specific pattern that the model learns, which helps it determine the position of each word, or the distance between different words in the sequence.
- 💡 Intuition: adding these values to the embeddings provides meaningful distances between the embedding vectors once they’re projected into // vectors and during dot-product attention.
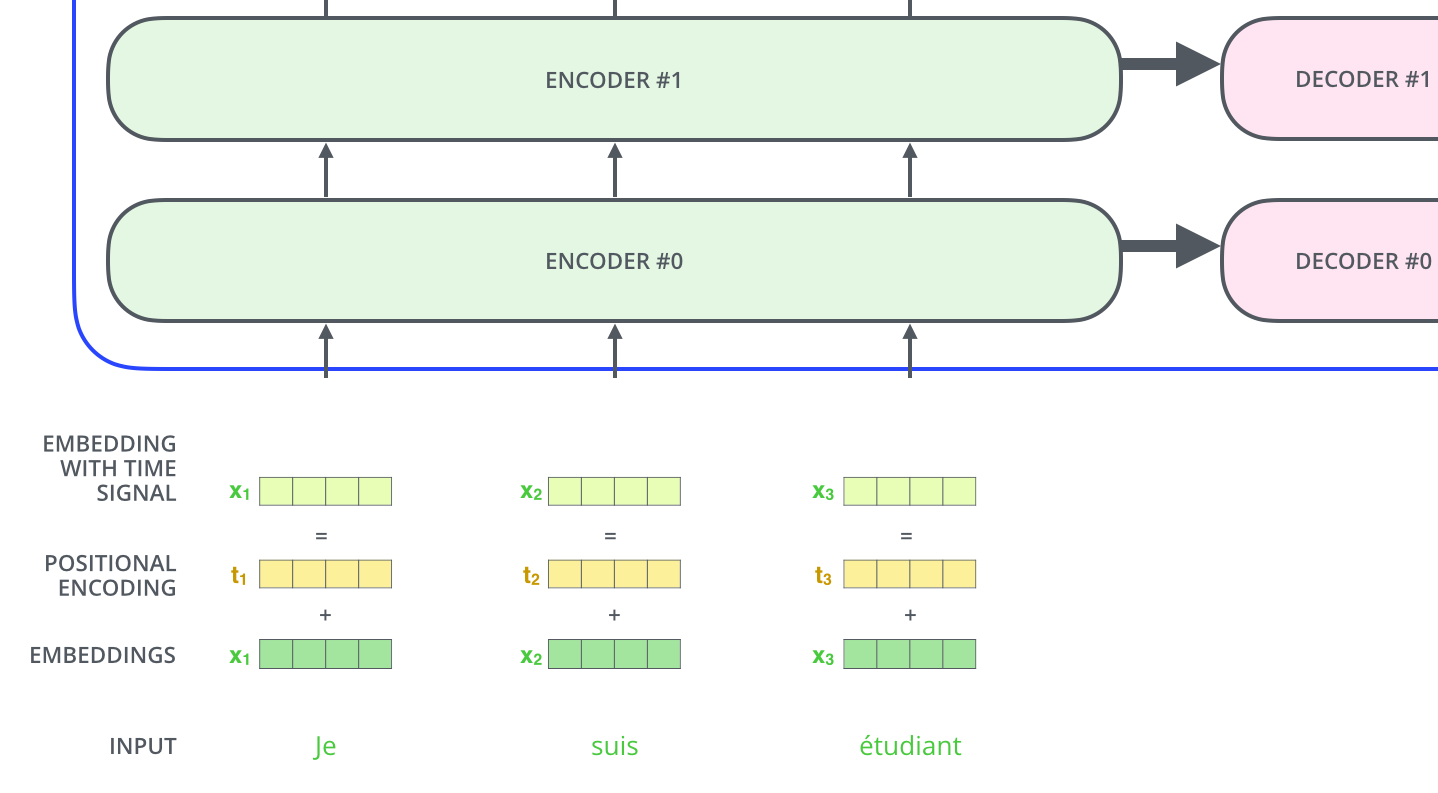
To give the model a sense of the order of the words, we add positional encoding vectors – the values of which follow a specific pattern.
For instance, if we assumed the embedding has a dimensionality of 4, the actual positional encodings would look like this:
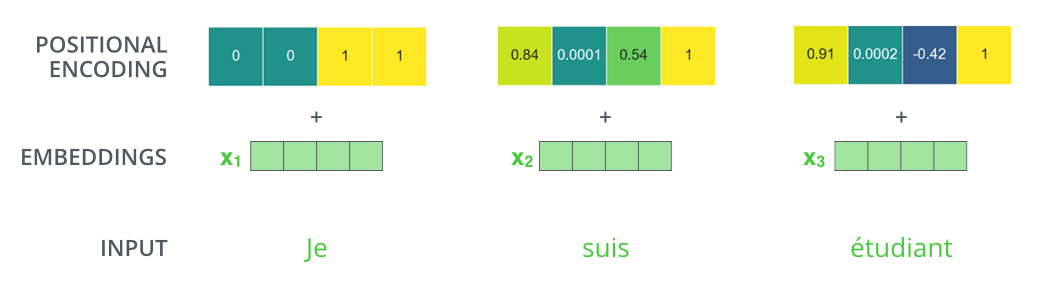
A real example of positional encoding with a toy embedding size of 4
What might this pattern look like?
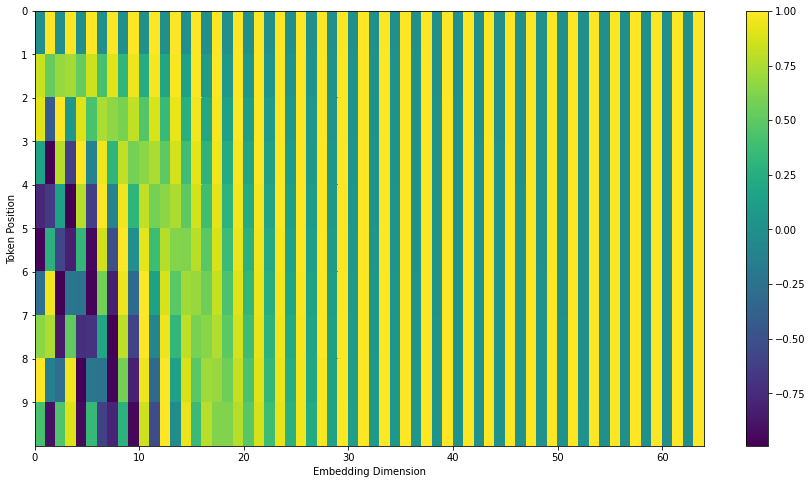
In the following figure, each row corresponds the a positional encoding of a vector.
- The first row would be the vector we’d add to the embedding of the first word in an input sequence.
- Each row contains 512 values – each with a value between 1 and -1.
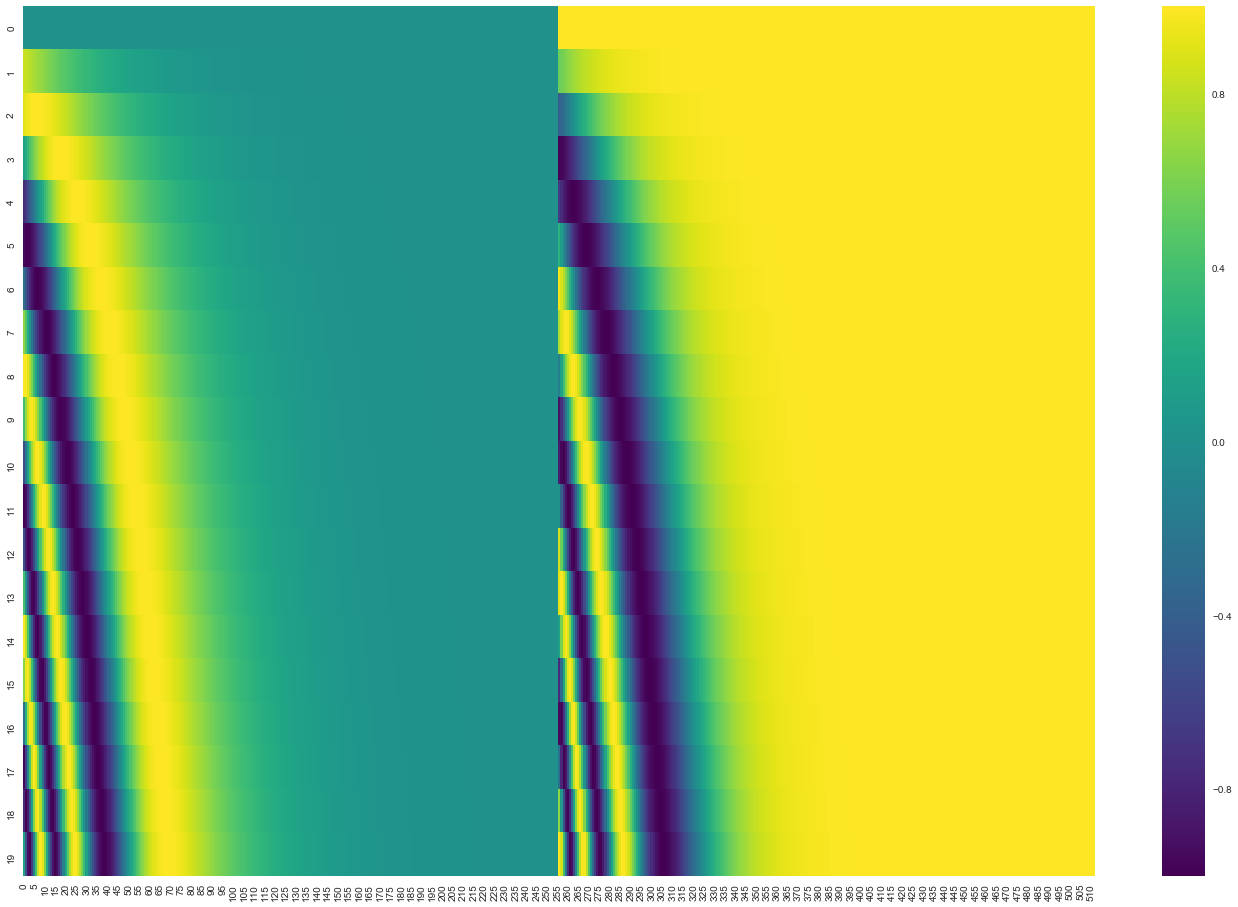
A real example of positional encoding for 20 words (rows) with an embedding size of 512 (columns). You can see that it appears split in half down the center. That’s because the values of the left half are generated by one function (which uses sine), and the right half is generated by another function (which uses cosine). They’re then concatenated to form each of the positional encoding vectors.
July 2020 Update: The positional encoding shown above is from the Tranformer2Transformer implementation of the Transformer. The method shown in the paper is slightly different in that it doesn’t directly concatenate, but interweaves the two signals. The following figure shows what that looks like.
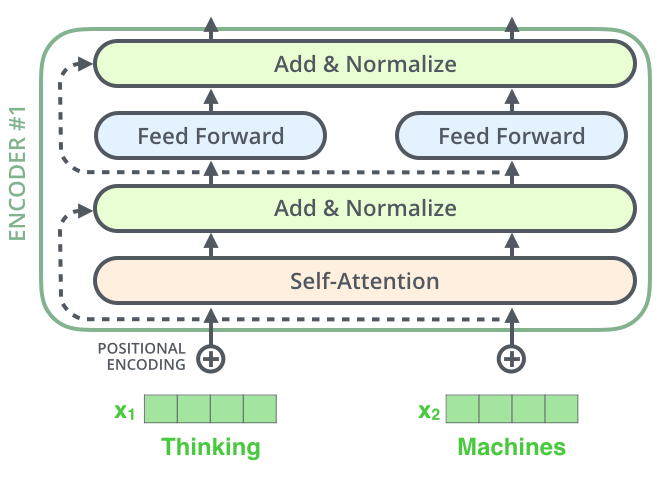
The Residuals
Each sub-layer (self-attention, FFNN) in each encoder has a residual connection around it, and is followed by a layer-normalization step.
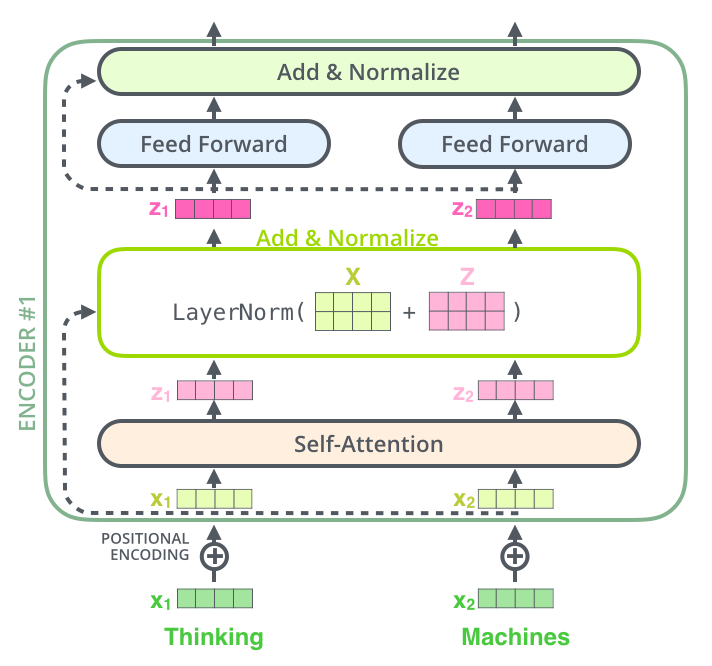
Visualize the vectors and the layer-norm operation associated with self attention
This goes for the sub-layers of the decoder as well.
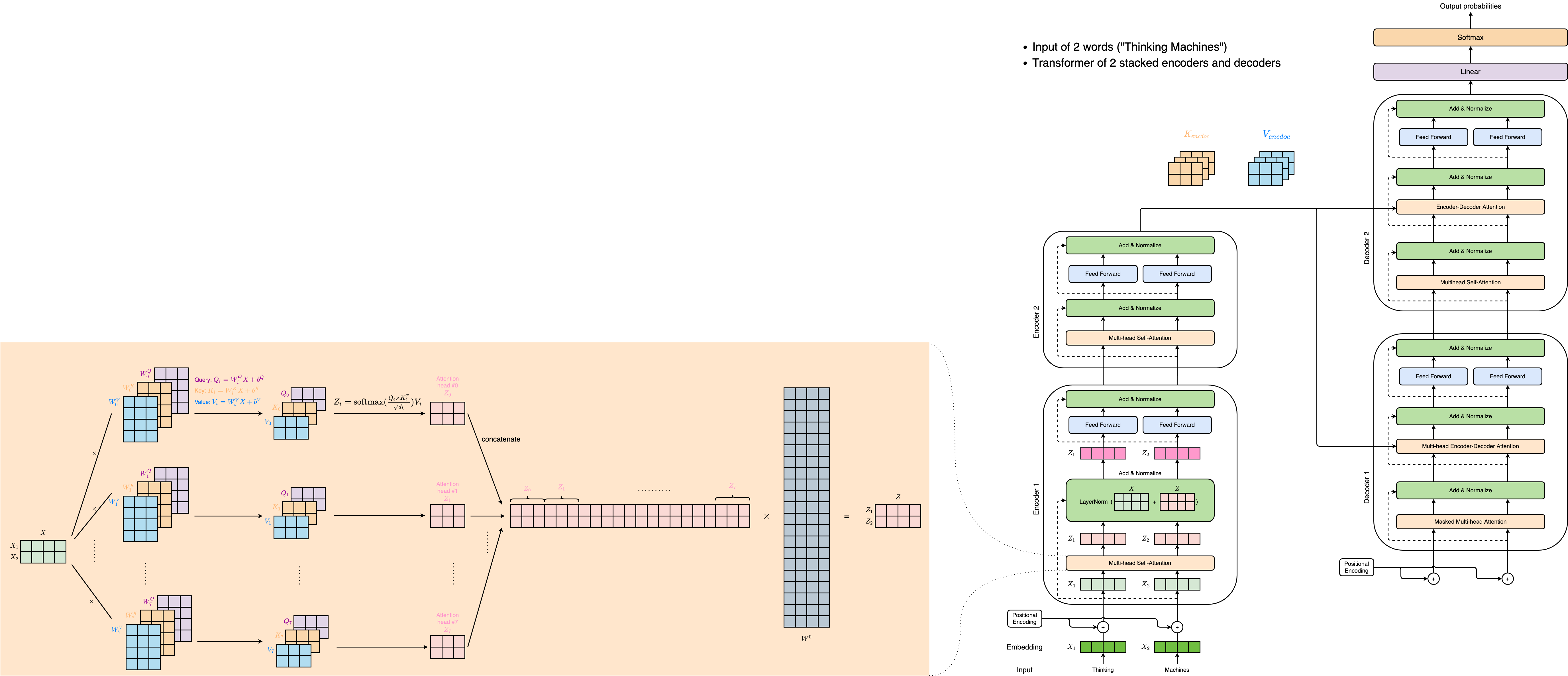
If we’re to think of a Transformer of 2 stacked encoders and decoders, it would look something like this:
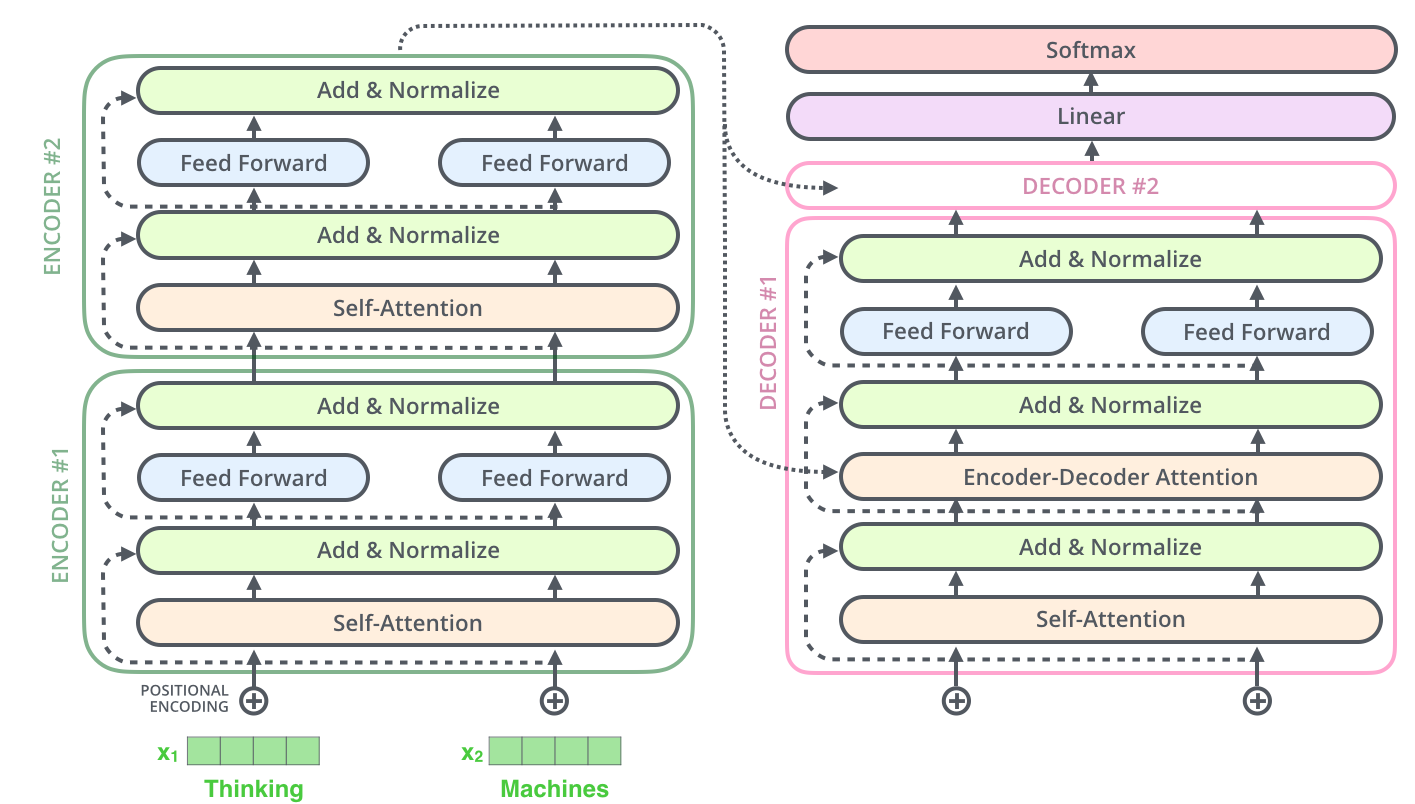
Decoding Component
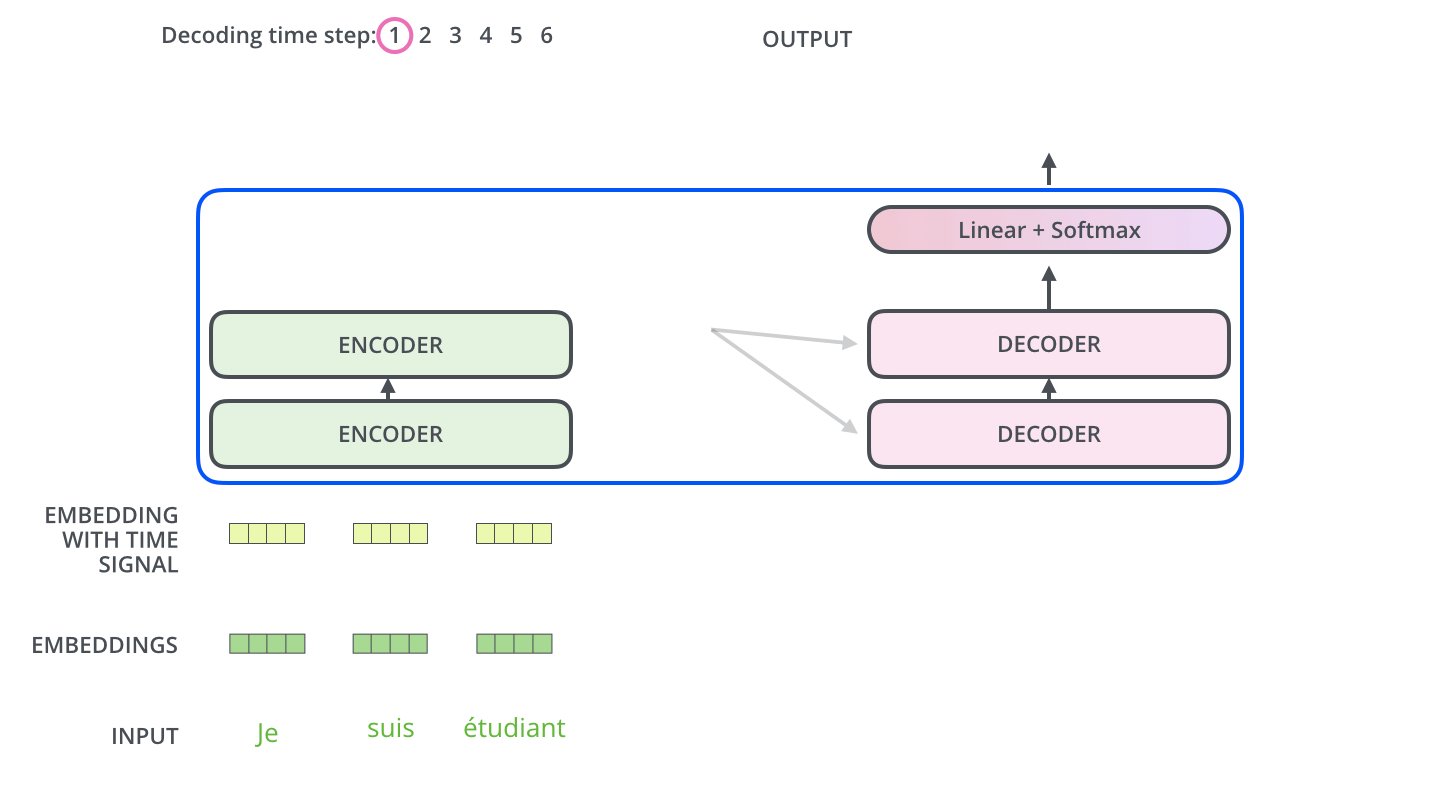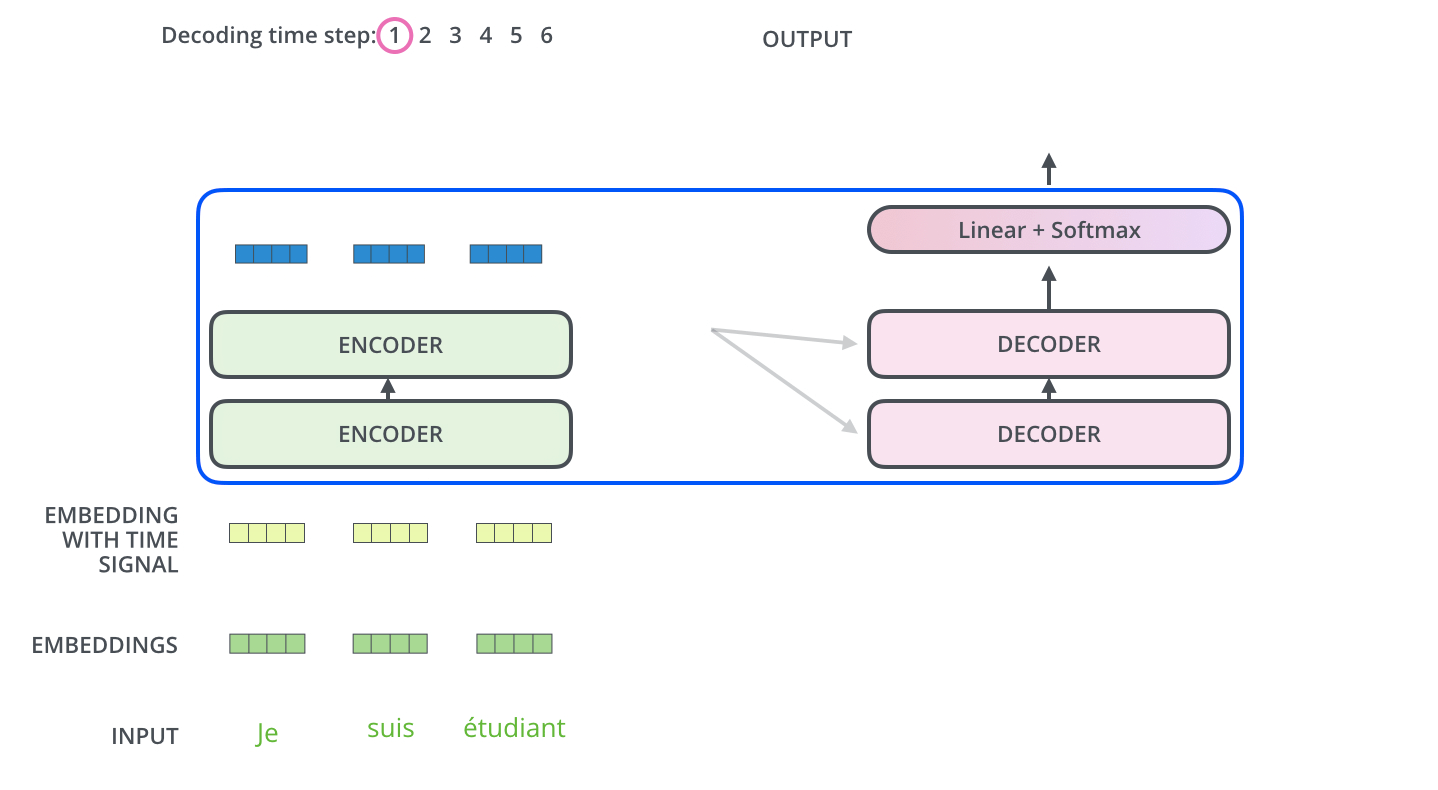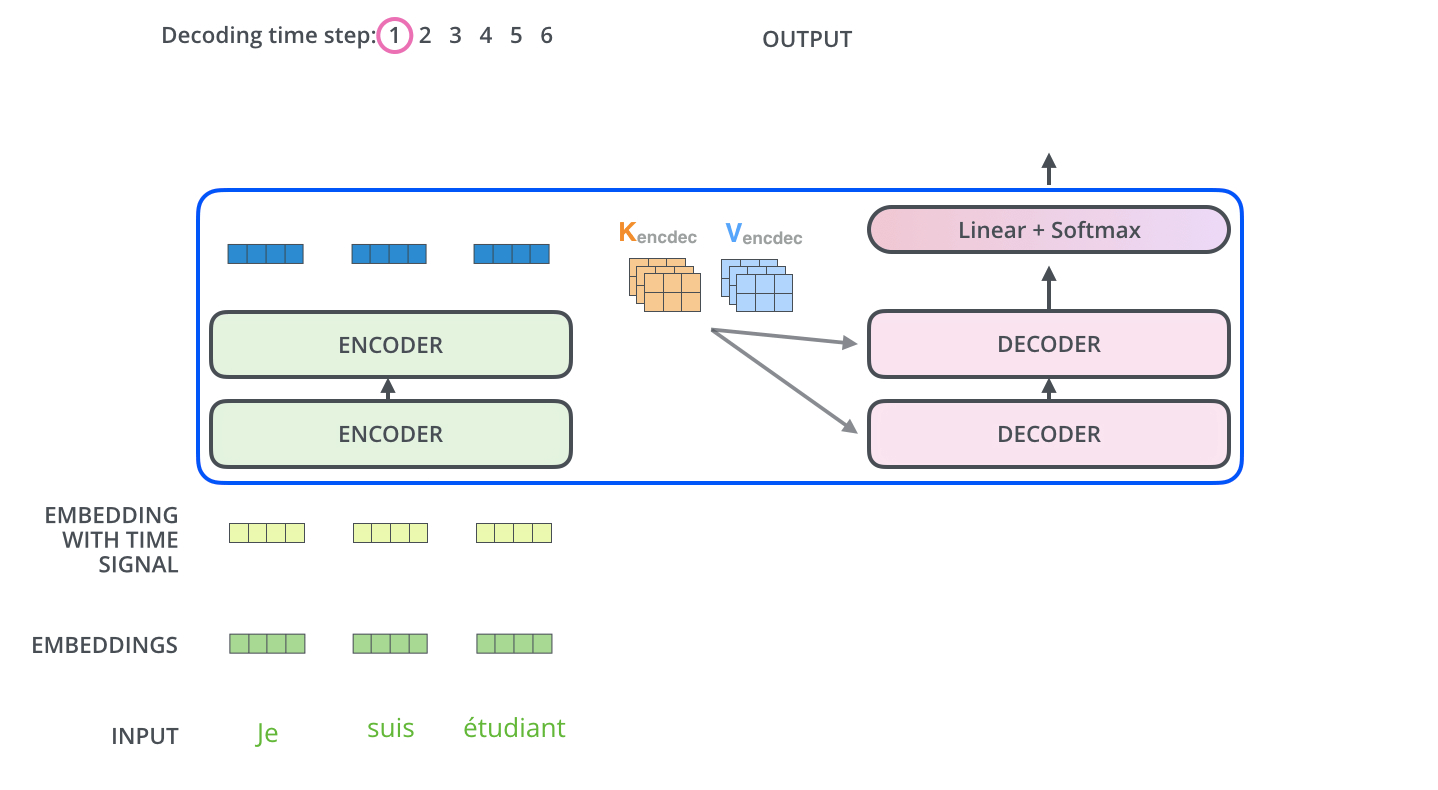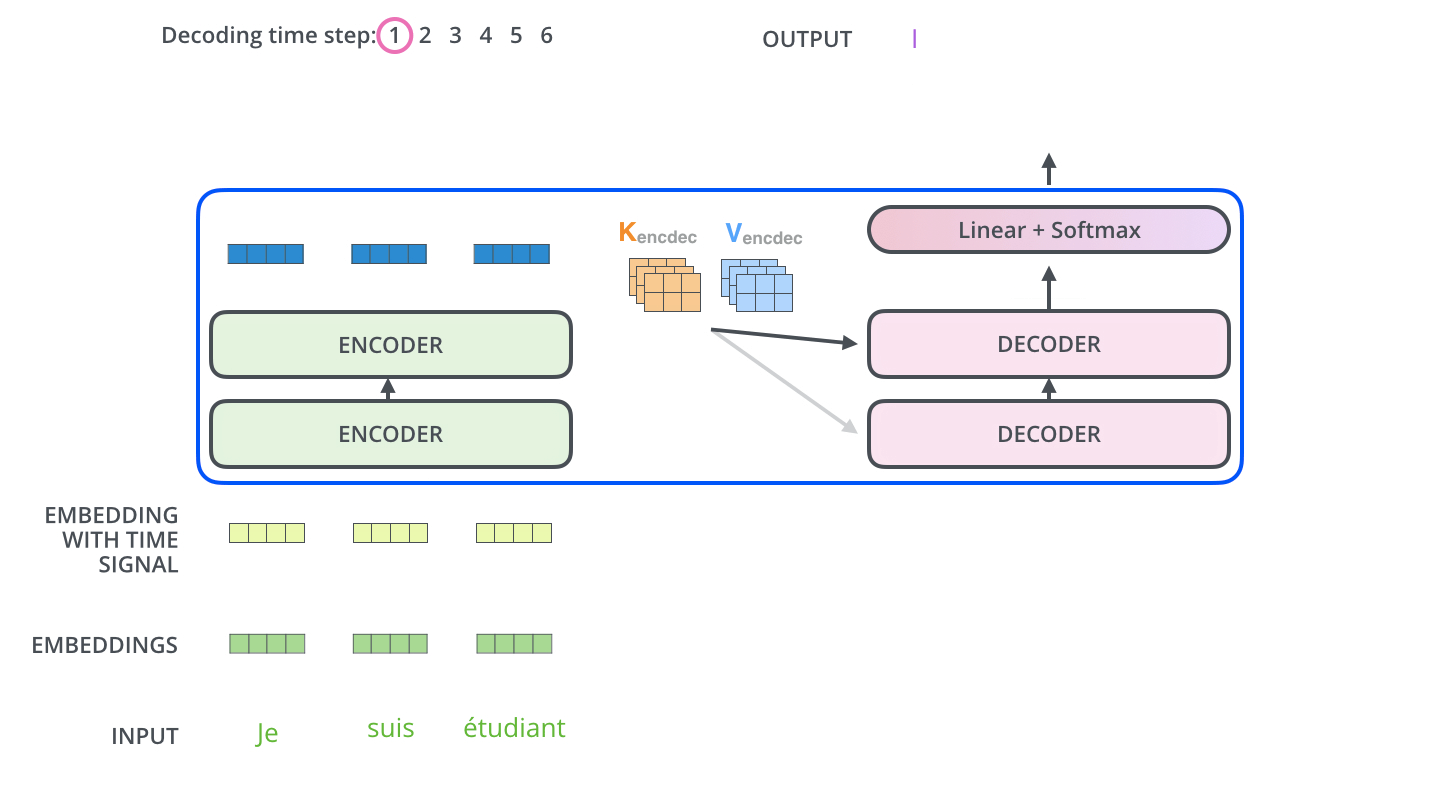
After finishing the encoding phase, we begin the decoding phase. Each step in the decoding phase outputs an element from the output sequence (the English translation sentence in this case).
- The encoder start by processing the input sequence.
- The output of the top encoder is then transformed into a set of attention vectors and .
- These are to be used by each decoder in its “encoder-decoder attention” layer which helps the decoder focus on appropriate places in the input sequence
The following steps repeat the process until a special symbol <eos> is reached, indicating the transformer decoder has completed its output.
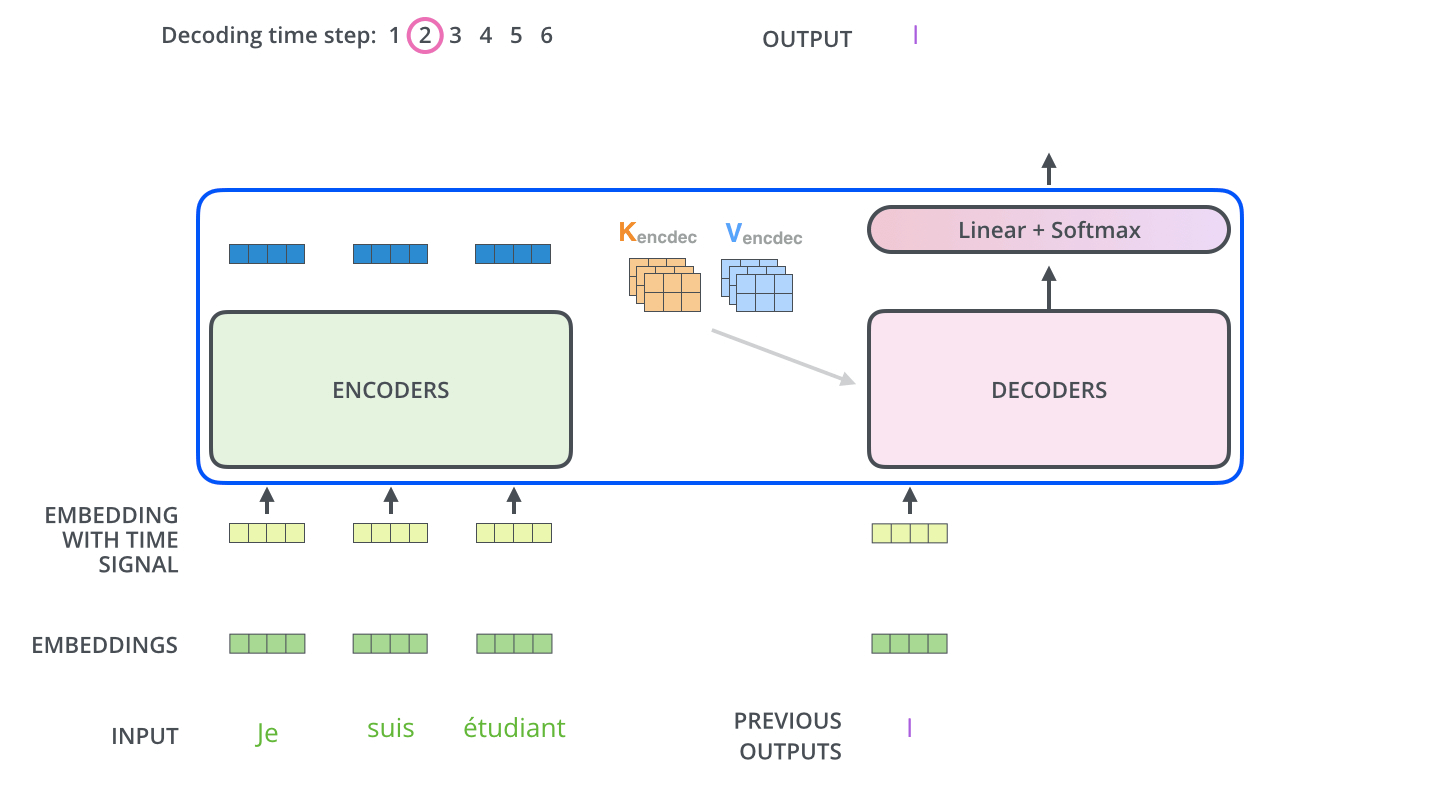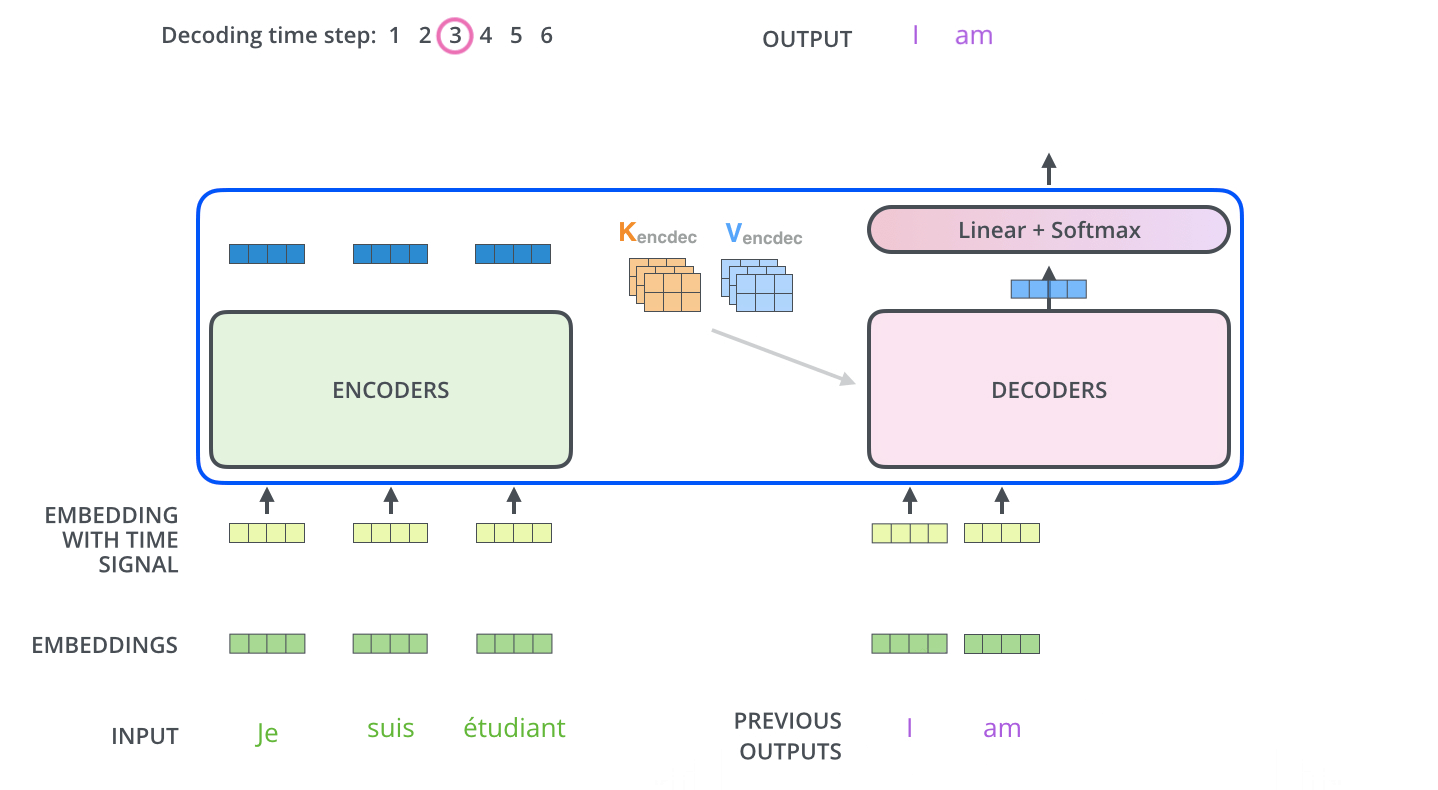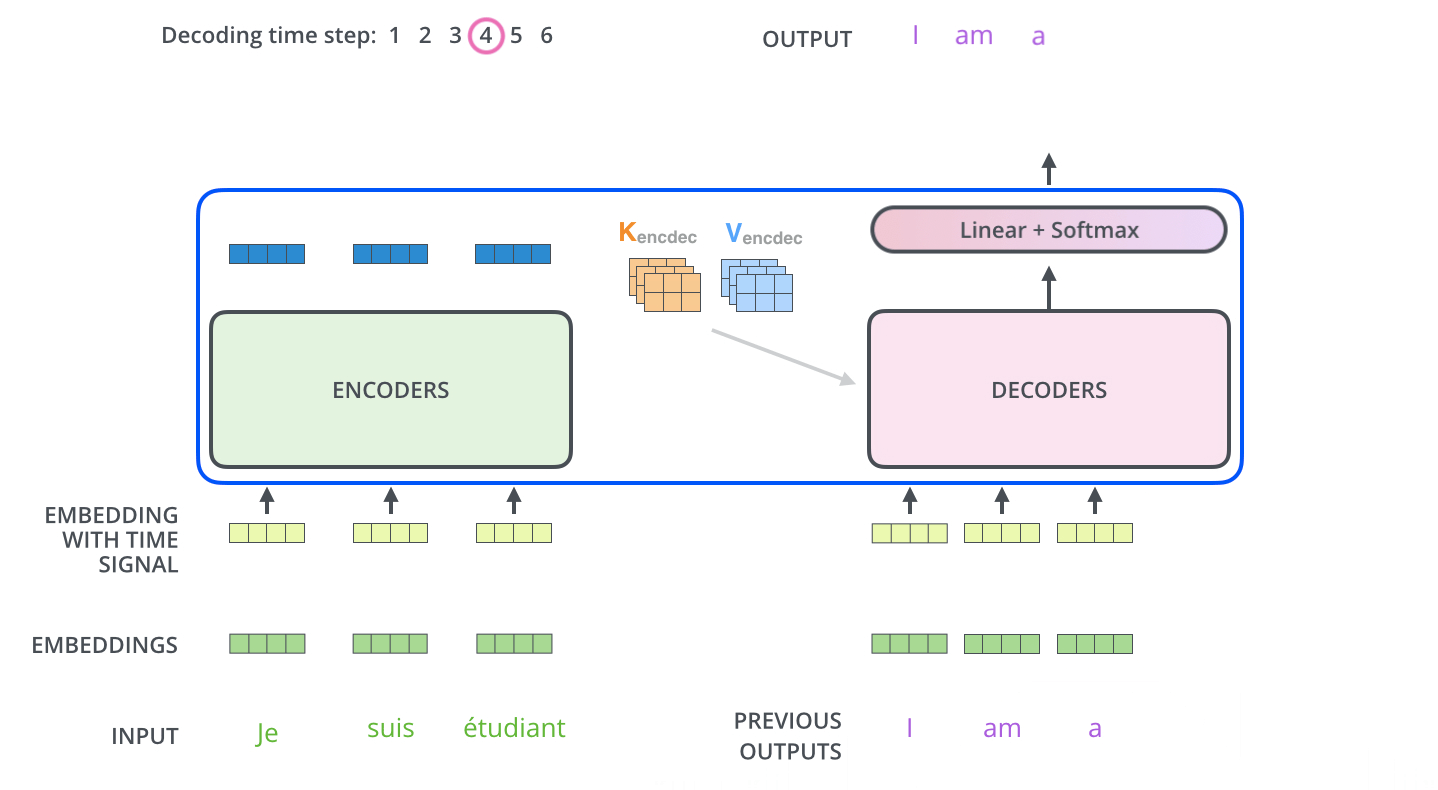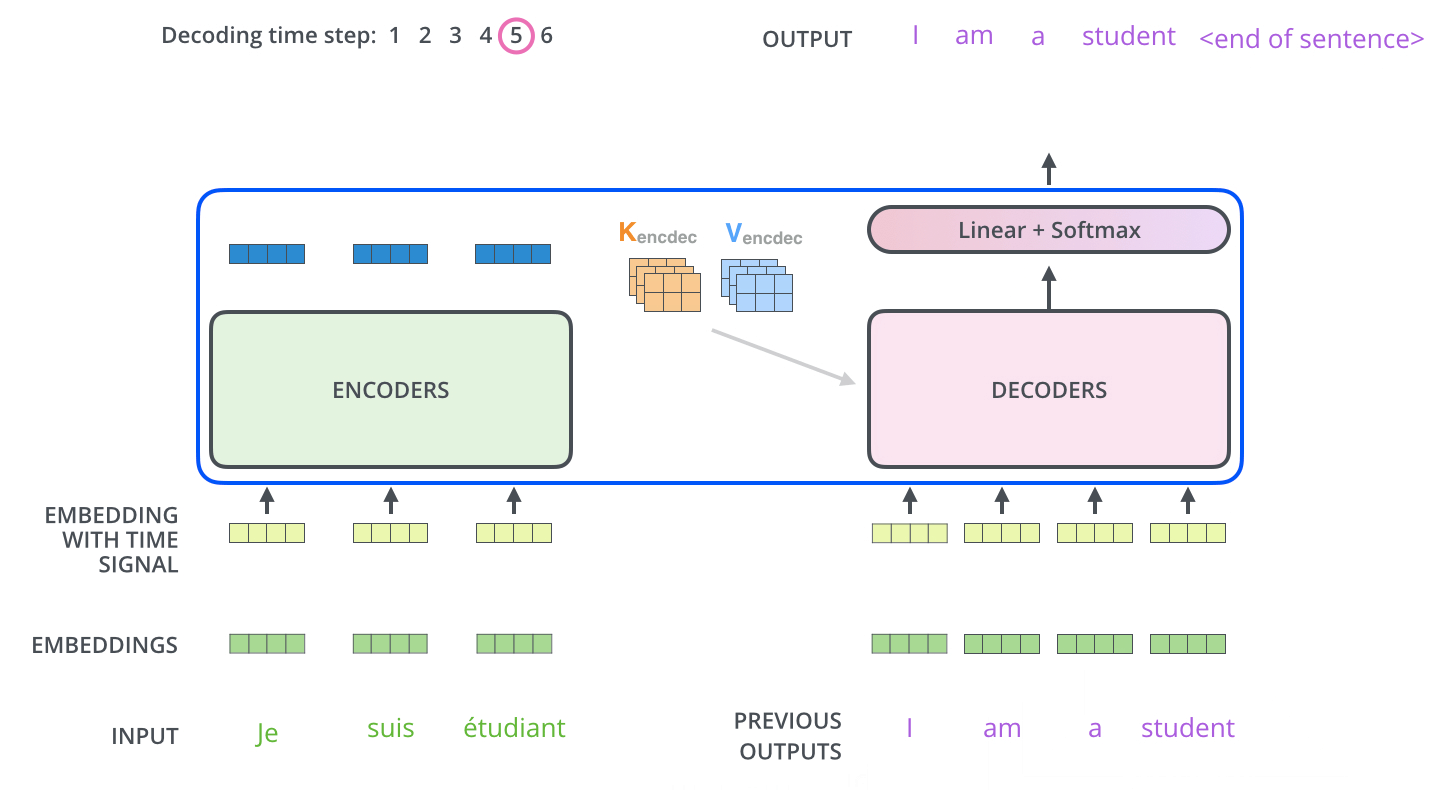
- The output of each step is fed to the bottom decoder in the next time step,
- The decoders bubble up their decoding results just like the encoders did.
- Just like we did with the encoder inputs, we embed and add positional encoding to those decoder inputs to indicate the position of each word.
Note that the self attention layers in the decoder operate in a slightly different way than the one in the encoder: In the decoder, the self-attention layer is ONLY allowed to attend to earlier positions in the output sequence.
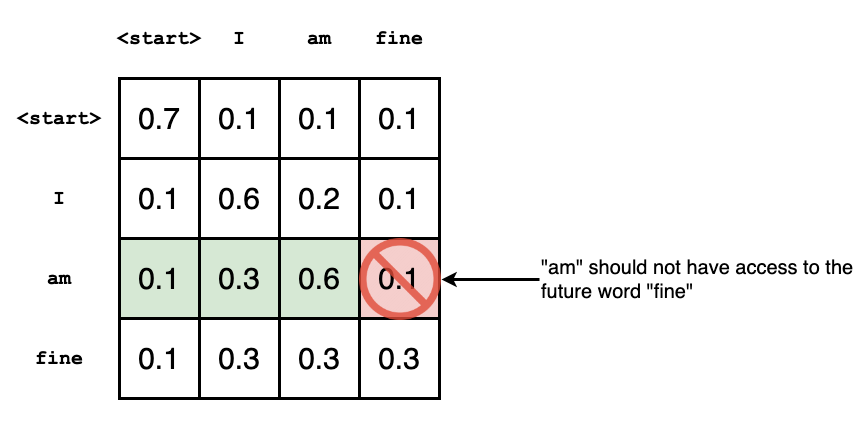
This can be done by masking future positions (setting them to
-inf) before the softmax step in the self-attention calculation.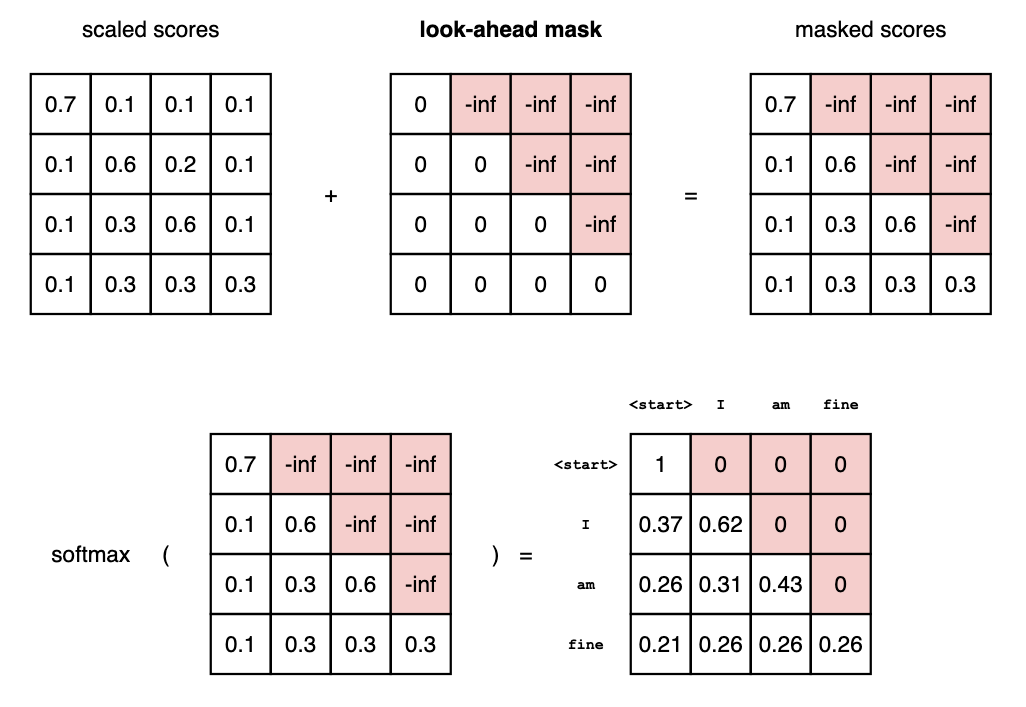
The attention scores for ‘am’ have values for itself and all other words before, but zero for the word ‘fine’. This essentially tells the model to put NO focus on the word ‘fine’.
The Final Linear and Softmax Layer
The final Linear layer + Softmax layer: Turn a vector of floats (the output of the decoder) into a word
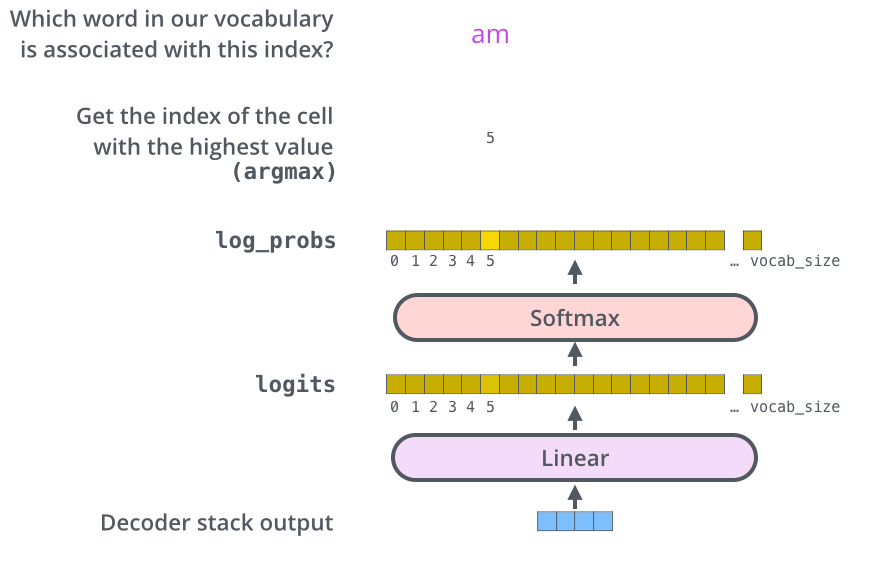
- Linear layer: a simple fully connected neural network that projects the vector produced by the stack of decoders, into a much, much larger vector called a logits vector
- Let’s assume that our model knows 10,000 unique English words (our model’s “output vocabulary”) that it’s learned from its training dataset. This would make the logits vector 10,000 cells wide – each cell corresponding to the score of a unique word.
- Softmax layer
- Turns those scores into probabilities (all positive, all add up to 1.0).
- The cell with the highest probability is chosen, and the word associated with it is produced as the output for this time step.
Training
Word Representation
During training, an untrained model would go through the exact same forward pass. Since we are training it on a labeled training dataset, we can compare its output with the actual correct output.
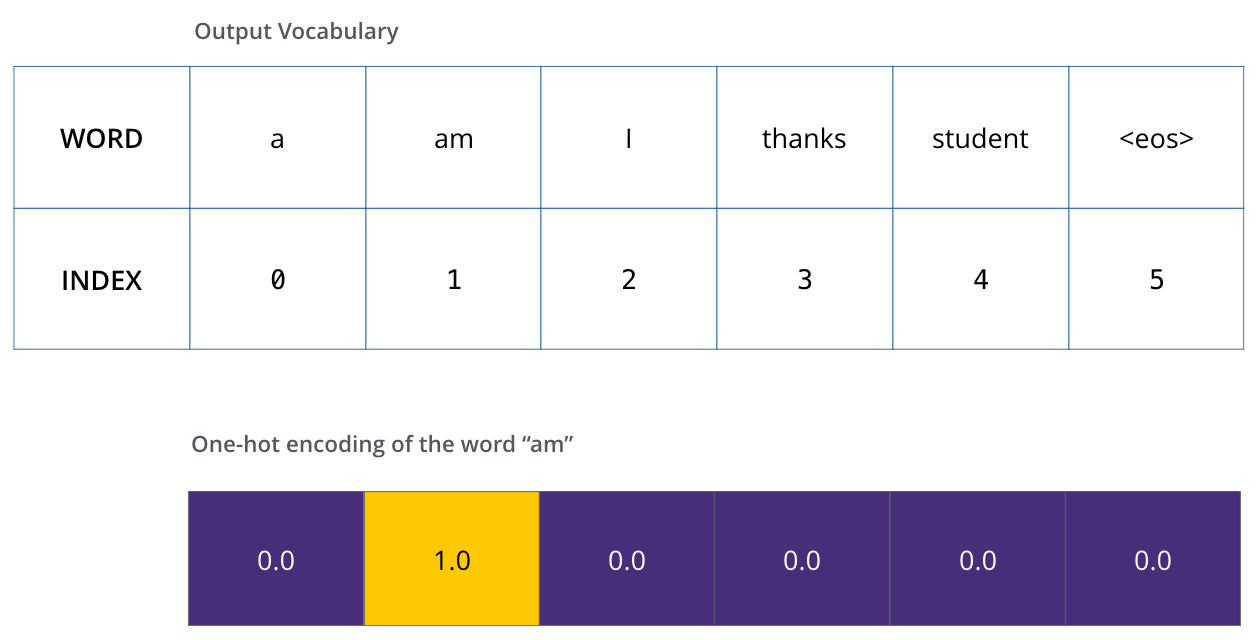
To visualize this, let’s assume our output vocabulary only contains six words: “a”, “am”, “i”, “thanks”, “student”, and “<eos>” (short for ‘end of sentence’).
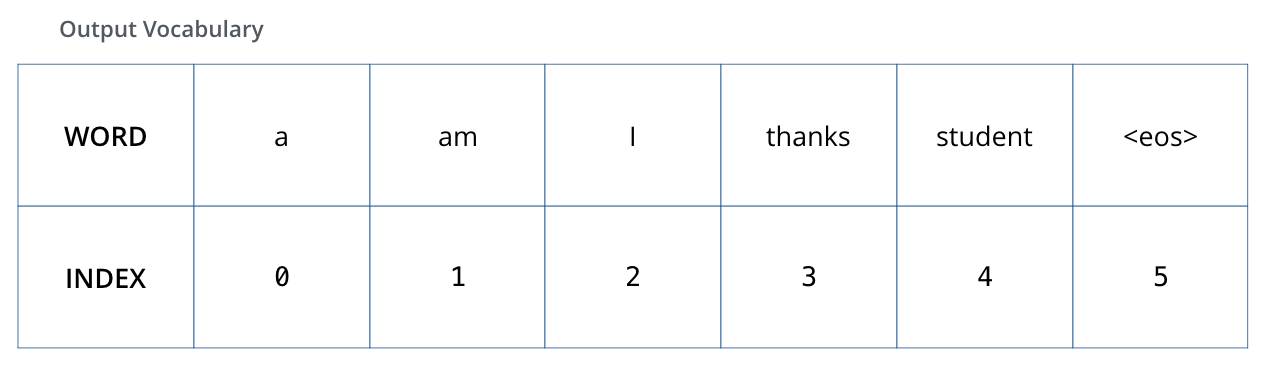
The output vocabulary of our model is created in the preprocessing phase before we even begin training.
After defining the output vocabulary, use One-Hot-encoding to indicate each word in our vocabulary. E.g., we can indicate the word “am” using the following vector:
The Loss Function
Say it’s our first step in the training phase, and we’re training it on a simple example – translating “merci” into “thanks”.
We want the output to be a probability distribution indicating the word “thanks”. But since this model is not yet trained, that’s unlikely to happen just yet.
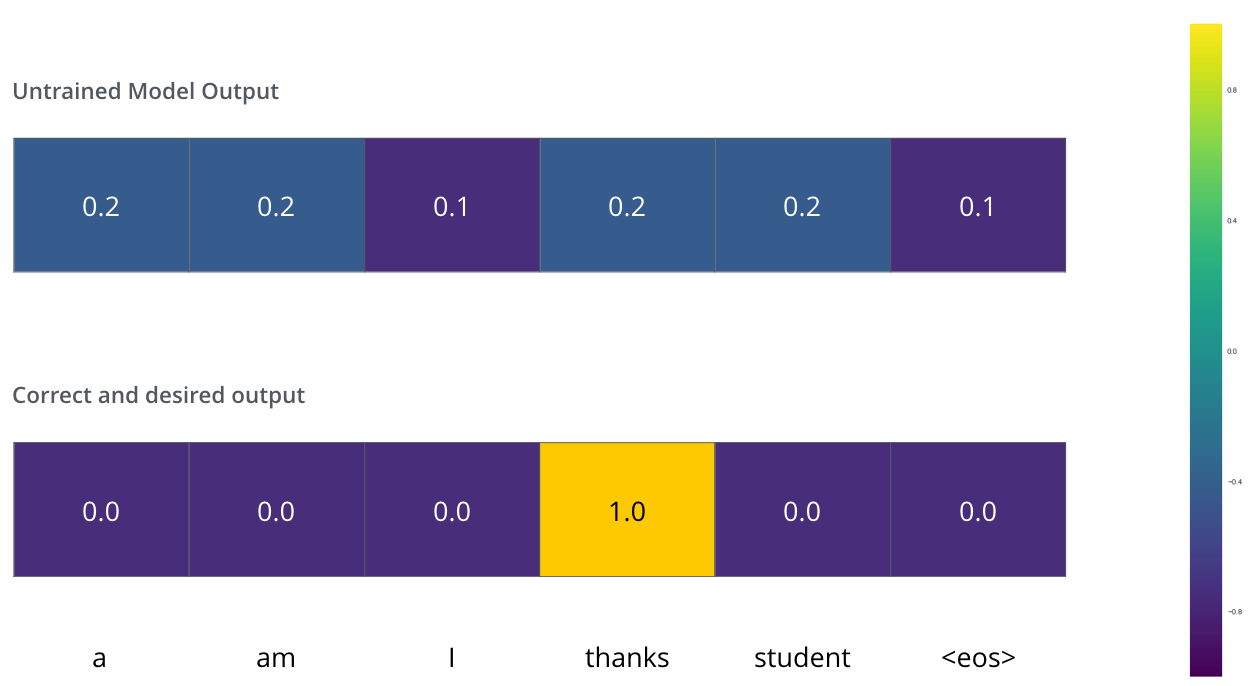
Since the model’s parameters (weights) are all initialized randomly, the (untrained) model produces a probability distribution with arbitrary values for each cell/word. We can compare it with the actual output, then tweak all the model’s weights using backpropagation to make the output closer to the desired output.
Compare two probability distributions: simply subtract one from the other. (For more details, look at cross-entropy and Kullback–Leibler divergence.)
Note that the example above is an oversimplified example.
In practice, we’ll use a sentence longer than one word. For example
- input: “je suis étudiant” and
- expected output: “i am a student”.
What this really means, is that we want our model to successively output probability distributions where:
Each probability distribution is represented by a vector of width vocab_size (6 in our toy example, but more realistically a number like 30,000 or 50,000)
The first probability distribution has the highest probability at the cell associated with the word “i”
The second probability distribution has the highest probability at the cell associated with the word “am”
And so on, until the fifth output distribution indicates ‘
<end of sentence>’ symbol, which also has a cell associated with it from the 10,000 element vocabulary.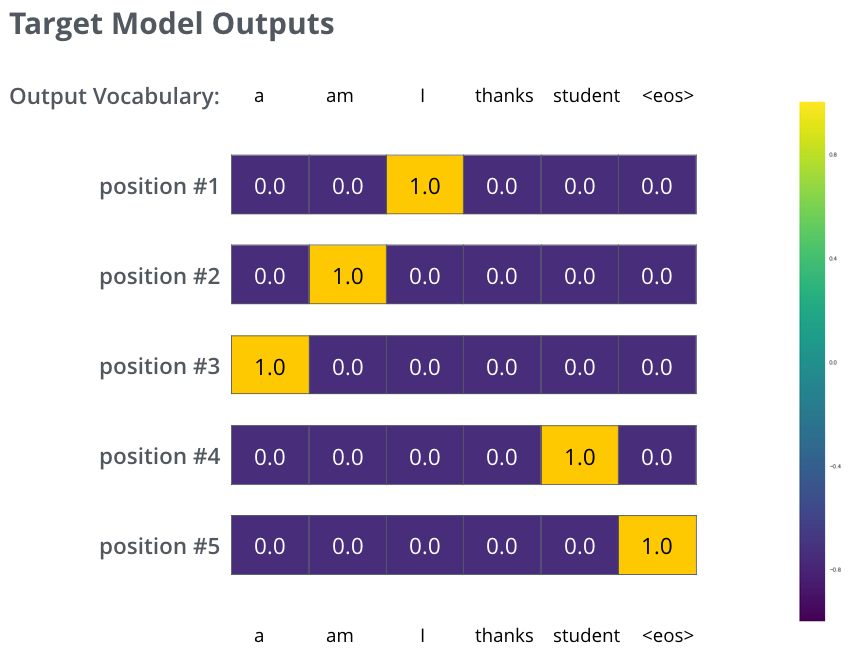
The targeted probability distributions we’ll train our model against in the training example for one sample sentence.
After training the model for enough time on a large enough dataset, we would hope the produced probability distributions would look like this:
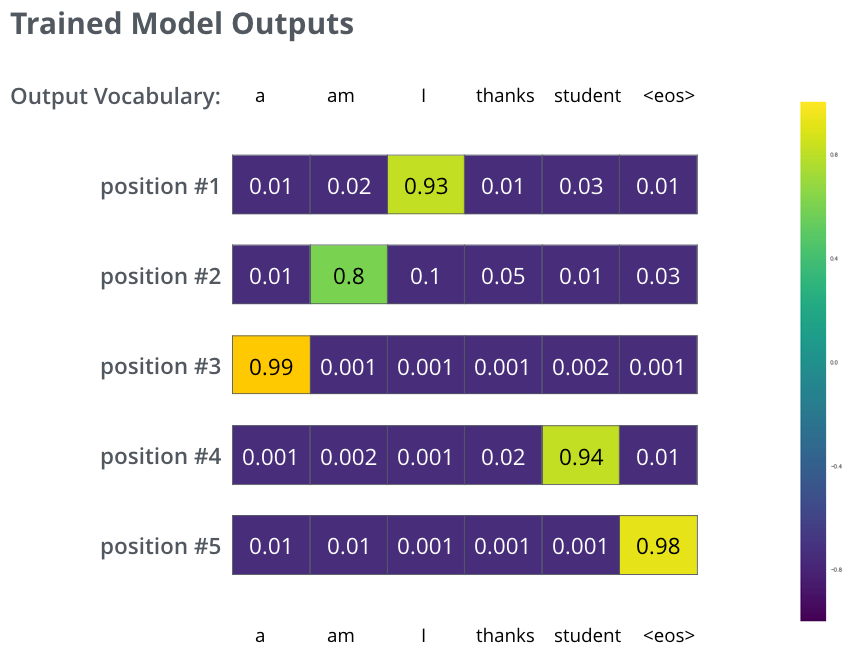
Now, because the model produces the outputs one at a time, we can assume that the model is selecting the word with the highest probability from that probability distribution and throwing away the rest (“greedy decoding”).
Reference
- The Illustrated Transformer - great explanation with a number of illustrations 👍🔥
- Paper: Attention is All You Need
- Pytorch implementation: guide annotating the paper with PyTorch implementation