👍 Activation Functions

Activation functions should be

• non-linear
• differentiable (since training with Backpropagation)

Sigmoid

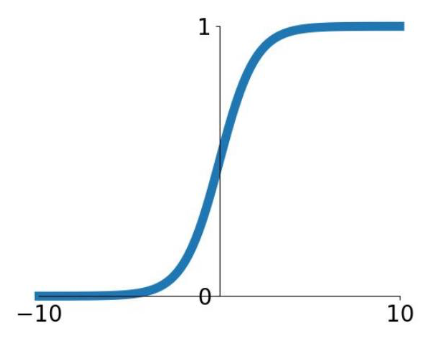
• Squashes numbers to range $[0,1]$

• ✅ Historically popular since they have nice interpretation as a saturating “firing rate” of a neuron

• ⛔️ Problems

  • Vanishing gradients: functions gradient at either tail of $1$ or $0$ is almost zero
  • Sigmoid outputs are not zero-centered (important for initialization)
  • $\exp()$ is a bit compute expensive

• Derivative

  $$\frac{d}{dx} \sigma(x) = \sigma(x)(1 - \sigma(x))$$

  (See: Derivative of Sigmoid Function)

• Python implementation

  def sigmoid(x):
      return 1 / (1 + np.exp(-x))
  

  Copy

  • Derivative

    def dsigmoid(y):
        return y * (1 - y)
    

    Copy

Tanh

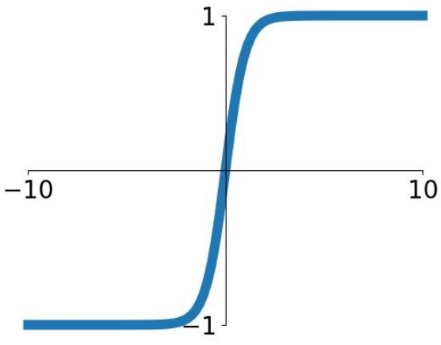
• Squashes numbers to range $[-1,1]$

• ✅ zero centered (nice) 👏

• ⛔️ Vanishing gradients: still kills gradients when saturated

• Derivative:

  $$\frac{d}{dx}\tanh(x) = 1 - [\tanh(x)]^2$$

  def dtanh(y):
      return 1 - y * y
  

  Copy

Rectified Linear Unit (ReLU)

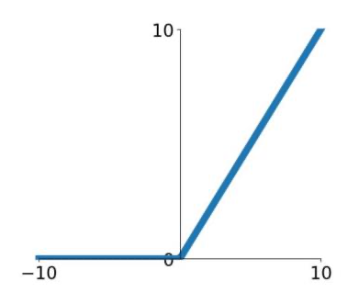
• ✅ Advantages

  • Does not saturate (in $[0, \infty]$)
  • Very computationally efficient
  • Converges much faster than sigmoid/tanh in practice

• ⛔️ Problems

  • Not zero-centred output
  • No gradient for $x < 0$ (dying ReLU)

• Python implementation

  import numpy as np
  
  def ReLU(x):
  	return np.maximum(0, x)
  

  Copy

Leaky ReLU

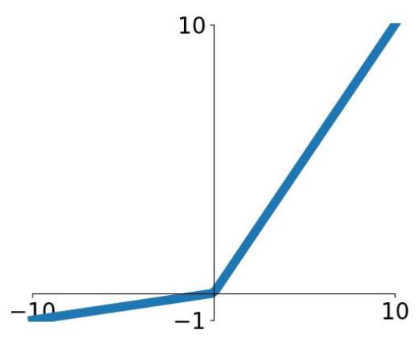
• Parametric Rectifier (PReLu)

  $$f(x) = \max(\alpha x, x)$$
  • Also learn $\alpha$

• ✅ Advantages

  • Does not saturate
  • Computationally efficient
  • Converges much faster than sigmoid/tanh in practice!
  • will not “die”

• Python implementation

  import numpy as np
  
  def ReLU(x):
  	return np.maximum(0.1 * x, x)
  

  Copy

Exponential Linear Units (ELU)

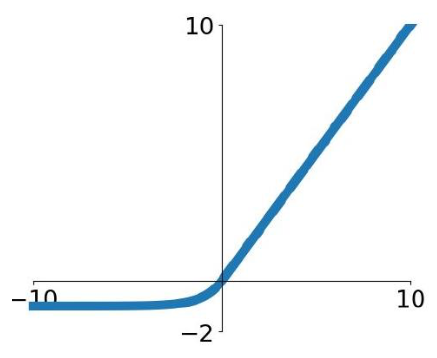
• ✅ Advantages
  • All benefits of ReLU
  • Closer to zero mean outputs
  • Negative saturation regime compared with Leaky ReLU (adds some robustness to noise)
• ⛔️ Problems
  • Computation requires $\exp()$

Maxout

• Generalizes ReLU and Leaky ReLU
  • ReLU is Maxout with $w\_1 =0$ and $b\_1 = 0$
• ✅ Fixes the dying ReLU problem
• ⛔️ Doubles the number of parameters

Softmax

• Softmax: probability that feature $x$ belongs to class $c\_k$ $$o\_k = \theta\_k^Tx \qquad \forall k = 1, \dots, j$$

• Derivative: $$\frac{\partial p(\hat{\mathbf{y}})}{\partial o\_{j}} =y\_{j}-p\left(\hat{y}\_{j}\right)$$

Advice in Practice

• Use ReLU
  • Be careful with your learning rates / initialization
• Try out Leaky ReLU / ELU / Maxout
• Try out tanh but don’t expect much
• Don’t use sigmoid

Summary and Overview

See: Wiki-Activation Function