Docs
AI
DL
NN Basics
MLP and Backprop

Multilayer Perceptron and Backpropagation

Multi-Layer Perceptron (MLP)

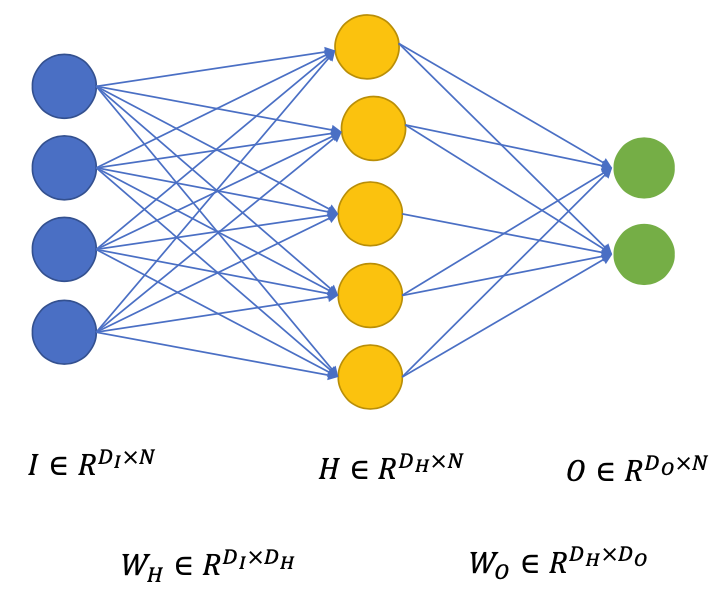
截屏2020-08-17 17.57.47

  • Input layer $I \in R^{D\_{I} \times N}$

    • How we initially represent the features

    • Mini-batch processing with $N$ inputs

  • Weight matrices

    • Input to Hidden: $W\_{H} \in R^{D\_{I} \times D\_{H}}$

    • Hidden to Output: $W\_{O} \in R^{D\_{H} \times D\_{O}}$

  • Hidden layer(s) $H \in R^{D\_{H} \times N}$

    $$ H = W\_{H}I + b\_H $$ $$ \widehat{H}\_j = f(H\_j) $$
    • $f$: non-linear activation function

  • Output layer $O \in R^{D\_{O} \times N}$

    • The value of the target function that the network approximates $$ O = W\_O \widehat{H} + b\_O $$

Backpropagation

  • Loss function

    $$ L = \frac{1}{2}(O - Y)^2 $$

    • Achieve minimum $L$: Stochastic Gradient Descent

      1. Calculate $\frac{\delta L}{\delta w}$ for each parameter $w$

      2. Update the parameters

        $$ w:=w-\alpha \frac{\delta L}{\delta w} $$

  • Compute the gradients: Backpropagation (Backprop)

    • Output layer
    $$ \begin{aligned} \frac{\delta L}{\delta O} &=(O-Y) \\\\ \\\\ \frac{\delta L}{\delta \widehat{H}} &=W\_{O}^{T} \color{red}{\frac{\delta L}{\delta O}} \\\\ \\\\ \frac{\delta L}{\delta W\_{O}} &= {\color{red}{\frac{\delta L}{\delta O} }}\widehat{H}^{T} \\\\ \\\\ \frac{\delta L}{\delta b\_{O}} &= \color{red}{\frac{\delta L}{\delta O}} \end{aligned} $$

    ​ (Red: terms previously computed)

    • Hidden layer (assuming $\widehat{H}=\operatorname{sigmoid}(H)$ )

      $$ \frac{\delta L}{\delta H}={\color{red}{\frac{\delta L}{\delta \hat{H}}}} \odot \widehat{H} \odot(1-\widehat{H}) $$

      ($\odot$: element-wise multiplication)

    • Input layer

    $$ \begin{array}{l} \frac{\delta L}{\delta W\_{H}}={\color{red}{\frac{\delta L}{\delta H}}} I^{T} \\\\ \\\\ \frac{\delta L}{\delta b\_{H}}={\color{red}{\frac{\delta L}{\delta H}}} \end{array} $$

Gradients for vectorized operations

When dealing with matrix and vector operations, we must pay closer attention to dimensions and transpose operations.

Matrix-Matrix multiply gradient. Possibly the most tricky operation is the matrix-matrix multiplication (which generalizes all matrix-vector and vector-vector) multiply operations:

(Example from cs231n)

# forward pass
W = np.random.randn(5, 10)
X = np.random.randn(10, 3)
D = W.dot(X)

# now suppose we had the gradient on D from above in the circuit
dD = np.random.randn(*D.shape) # same shape as D
dW = dD.dot(X.T) #.T gives the transpose of the matrix
dX = W.T.dot(dD)

Tip: use dimension analysis!

Note that you do not need to remember the expressions for dW and dX because they are easy to re-derive based on dimensions.

For instance, we know that the gradient on the weights dW must be of the same size as W after it is computed, and that it must depend on matrix multiplication of X and dD (as is the case when both X,W are single numbers and not matrices). There is always exactly one way of achieving this so that the dimensions work out.

For example, X is of size [10 x 3] and dD of size [5 x 3], so if we want dW and W has shape [5 x 10], then the only way of achieving this is with dD.dot(X.T), as shown above.

For discussion of math details see: Not understanding derivative of a matrix-matrix product.