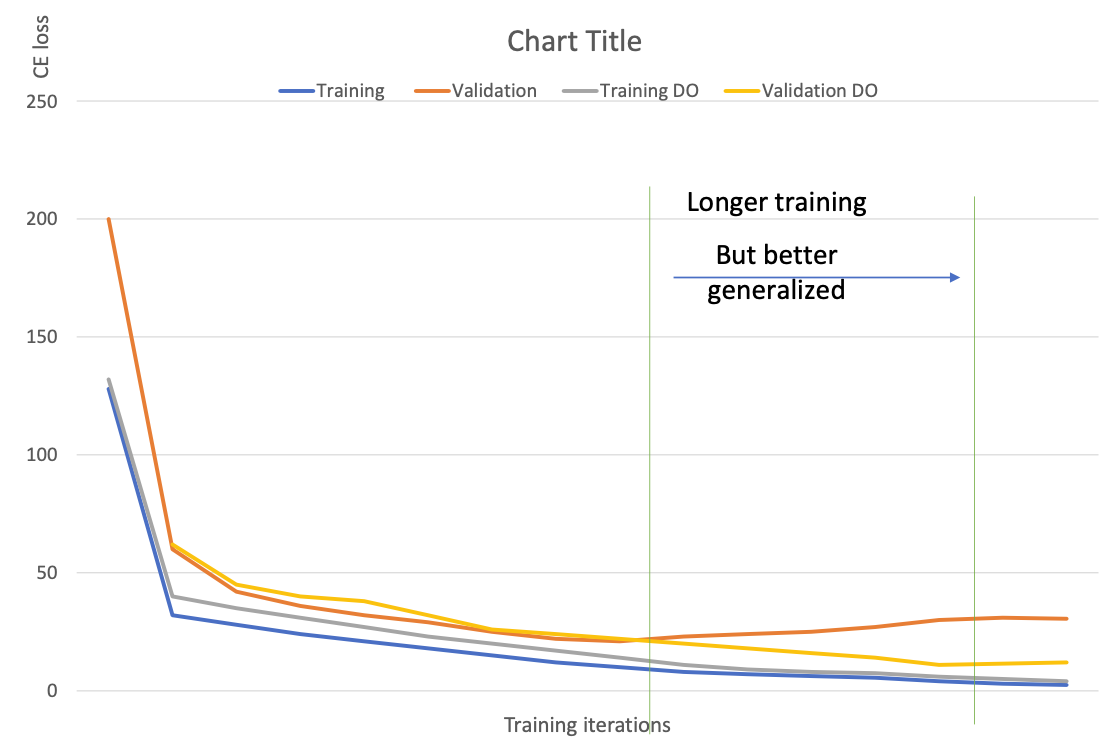
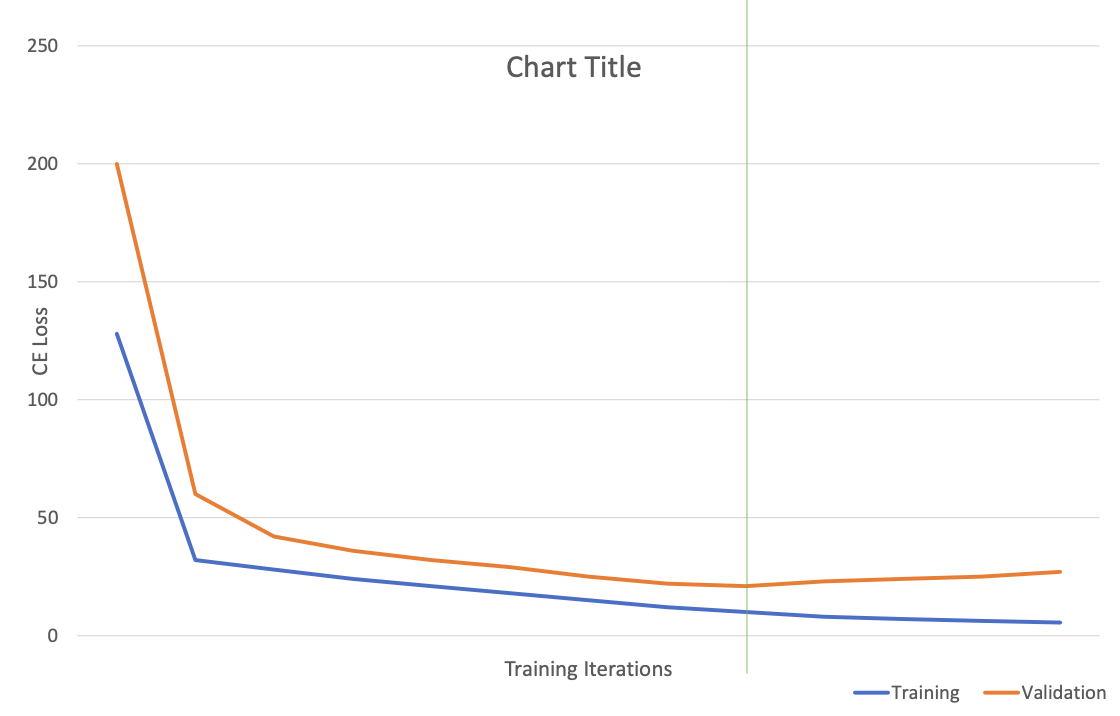
Dropout

Model Overfitting

In order to give more “capacity” to capture different features, we give neural nets a lot of neurons. But this can cause overfitting.

Reason: Co-adaptation

• Neurons become dependent on others
• Imagination: neuron $H\_i$ captures a particular feature $X$ which however, is very frequenly seen with some inputs.
  • If $H\_i$ receives bad inputs (partial of the combination), then there is a chance that the feature is ignored 🤪

Solution: Dropout! 💪

Dropout

With dropout the layer inputs become more sparse, forcing the network weights to become more robust.

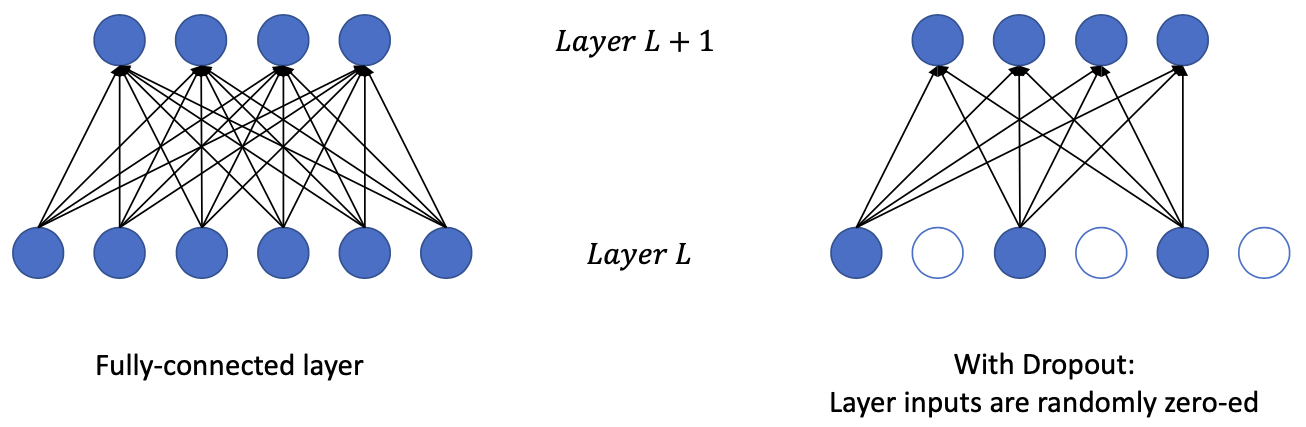
Dropout a neuron = all the inputs and outputs to this neuron will be disabled at the current iteration.

Training

• Given

  • input $X \in \mathbb{R}^D$
  • weights $W$
  • survival rate $p$
    • Usually $p=0.5$

• Sample mask $M \in \{0, 1\}^D$ with $M\_i \sim \operatorname{Bernoulli}(p)$

• Dropped input:

  $$\hat{X} = X \circ M$$

• Perform backward pass and mask the gradients:

  $$\frac{\delta L}{\delta X}=\frac{\delta L}{\delta \hat{X}} \circ M$$

Evaluation/Testing/Inference

• ALL input neurons $X$ are presented WITHOUT masking

• Because each neuron appears with probability $p$ in training

  $\to$ So we have to scale $X$ with $p$ (or scale $\hat{X}$ with $\frac{1}{1-p}$ during training) to match its expectation

Why Dropout works?

• Intuition: Dropout prevents the network to be too dependent on a small number of neurons, and forces every neuron to be able to operate independently.
• Each of the “dropped” instance is a different network configuration
• $2^n$ different networks sharing weights
• The inference process can be understood as an ensemble of $2^n$ different configuration
• This interpretation is in-line with Bayesian Neural Networks