👍 Loss Functions

• Quantifies what it means to have a “good” model
• Different types of loss functions for different tasks, such as:
  • Classification
  • Regression
  • Metric Learning
  • Reinforcement Learning

Classification

• Classification: Predicting a discrete class label

• Negative log-likelihood loss (per sample $x$) / Cross-Entropy loss

  $$L(\boldsymbol{x}, y)=-\sum\_{j} y_{j} \log p\left(c\_{j} \mid \boldsymbol{x}\right)$$
  • Used in various multiclass classification methods for NN training

• Hinge Loss: used in Support Vector Machines (SVMs)

  $$L(x, y)=\sum\_{j} \max \left(0,1-x\_{i} y\_{i}\right)$$

Regression

• Regression: Predicting a one or multiple continuous quantities $y_1, \dots, y\_n$

• Goal: Minimize the distance between the predicted value $\hat{y}\_j$ and true values $y_j$

• L1-Loss (Mean Average Error)

  $$L(\hat{y}, y)=\sum\_{j}\left(\hat{y}\_{j}-x\_{j}\right)$$

• L2-Loss (Mean Square Error, MSE)

  $$L(\hat{y}, y)=\sum\_{j}\left(\hat{y}\_{j}-x\_{j}\right)^2$$

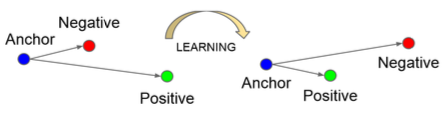
Metric Learning / Similarity Learning

• A model for measuring the distance (or similarity) between objects

• Triplet Loss

  

  \sum_{(a, p, n) \in T} \max \left\\{0, \alpha-\left\|\mathbf{x}\_{a}-\mathbf{x}\_{n}\right\|\_{2}^{2}+\left\|\mathbf{x}\_{a}-\mathbf{x}\_{p}\right\|\_{2}^{2}\right\\}