Docs
AI
DL
NN Basics
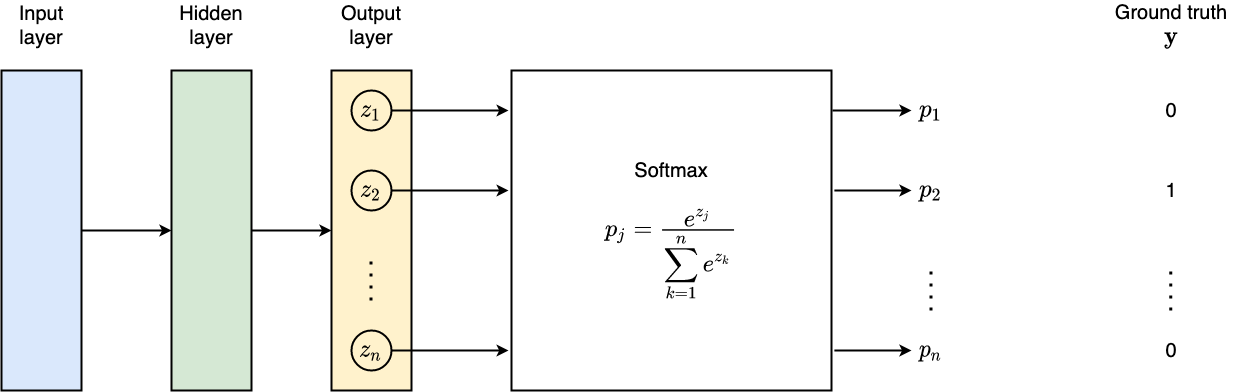
Math: Softmax

Softmax and Its Derivative

Softmax

Softmax

We use softmax activation function to predict the probability assigned to $n$ classes. For example, the probability of assigning input sample to $j$-th class is:

$$ p\_j = \operatorname{softmax}(z\_j) = \frac{e^{z\_j}}{\sum\_{k=1}^n e^{z\_k}} $$

Furthermore, we use One-Hot encoding to represent the groundtruth $y$, which means

$$ \sum\_{k=1}^n y\_k = 1 $$

Loss function (Cross-Entropy):

$$ \begin{aligned} L &= -\sum\_{k=1}^n y\_k \log(p\_k) \\\\ &= - \left(y\_j \log(p\_j) + \sum\_{k \neq j}y\_k \log(p\_k)\right) \end{aligned} $$

Gradient w.r.t $z\_j$:

$$ \begin{aligned} \frac{\partial}{\partial z\_j}L &= \frac{\partial}{\partial z\_j} \left(-\sum\_{k=1}^n y\_k \log(p\_k)\right) \\\\ &= -\frac{\partial}{\partial z\_j} \left(y\_j \log(p\_j) + \sum\_{k \neq j}y\_k \log(p\_k)\right) \\\\ &= -\left(\frac{\partial}{\partial z\_j} y\_j \log(p\_j) + \frac{\partial}{\partial z\_j}\sum\_{k \neq j}y\_k \log(p\_k)\right) \end{aligned} $$

  • $k=j$

    $$ \begin{aligned} \frac{\partial}{\partial z\_j} y\_j \log(p\_j) &= \frac{y\_j}{p\_j} \cdot \left(\frac{\partial}{\partial z\_j} p\_j\right) \\\\ &= \frac{y\_j}{p\_j} \cdot \left(\frac{\partial}{\partial z\_j} \frac{e^{z\_j}}{\sum\_{k=1}^n e^{z\_k}}\right) \\\\ &= \frac{y\_j}{p\_j} \cdot \frac{(\frac{\partial}{\partial z\_j}e^{z\_j})\sum\_{k=1}^n e^{z\_k} - e^{z\_j}(\frac{\partial}{\partial z\_j}\sum\_{k=1}^n e^{z\_k}) }{(\sum\_{k=1}^n e^{z\_k})^2} \\\\ &= \frac{y\_j}{p\_j} \cdot \frac{e^{z\_j}\sum\_{k=1}^n e^{z\_k} - e^{z\_j}e^{z\_j}}{(\sum\_{k=1}^n e^{z\_k})^2} \\\\ &= \frac{y\_j}{p\_j} \cdot \frac{e^{z\_j}(\sum\_{k=1}^n e^{z\_k} - e^{z\_j})}{(\sum\_{k=1}^n e^{z\_k})^2} \\\\ &= \frac{y\_j}{p\_j} \cdot \underbrace{\frac{e^{z\_j}}{\sum\_{k=1}^n e^{z\_k}}}\_{=p\_j} \cdot \frac{\sum\_{k=1}^n e^{z\_k} - e^{z\_j}}{\sum\_{k=1}^n e^{z\_k}}\\\\ &= \frac{y\_j}{p\_j} \cdot p\_j \cdot \underbrace{\left( \frac{\sum\_{k=1}^n e^{z\_k} }{\sum\_{k=1}^n e^{z\_k}} - \frac{e^{z\_j} }{\sum\_{k=1}^n e^{z\_k}}\right)}\_{=1 - p\_j} \\\\ &= y\_j(1-p\_j) \end{aligned} $$

  • $\forall k \neq j$

    $$ \begin{aligned} \frac{\partial}{\partial z\_j}\sum\_{k \neq j}y\_k \log(p\_k) &= \sum\_{k \neq j} \frac{\partial}{\partial z\_j}y\_k \log(p\_k) \\\\ &= \sum\_{k \neq j} \frac{y\_k}{p\_k} \cdot \frac{(\overbrace{\frac{\partial}{\partial z\_j} e^{z\_k}}^{=0})(\sum\_i e^{z\_i}) - e^{z\_k}(\overbrace{\frac{\partial}{\partial z\_j}\sum\_i e^{z\_i}}^{=e^{z\_j}})}{(\sum\_{k=1}^n e^{z\_k})^2} \\\\ &= \sum\_{k \neq j} \frac{y\_k}{p\_k} \frac{-e^{z\_k} e^{z\_j}}{(\sum\_{k=1}^n e^{z\_k})^2} \\\\ &= -\sum\_{k \neq j} \frac{y\_k}{p\_k} \underbrace{\frac{e^{z\_k}}{\sum\_{k=1}^n e^{z\_k}}}\_{=p\_k} \underbrace{\frac{e^{z\_j}}{\sum\_{k=1}^n e^{z\_k}}}\_{=p\_j} \\\\ &= -\sum\_{k \neq j}y\_kp\_j \end{aligned} $$

Therefore,

$$ \begin{aligned} \frac{\partial}{\partial z\_j}L &= -\left(\frac{\partial}{\partial z\_j} y\_j \log(p\_j) + \frac{\partial}{\partial z\_j}\sum\_{k \neq j}y\_k \log(p\_k)\right) \\\\ &= -\left(y\_j(1-p\_j) - \sum\_{k \neq j}y\_kp\_j\right) \\\\ &= -\left(y\_j-y\_jp\_j - \sum\_{k \neq j}y\_kp\_j\right) \\\\ &= -\left(y\_j- (y\_jp\_j + \sum\_{k \neq j}y\_kp\_j)\right) \\\\ &= -\left(y\_j- \sum\_{k=1}^ny\_kp\_j\right)\\\\ &\overset{\sum\_{k=1}^{n} y\_k = 1}{=} -\left(y\_j- p\_j\right) \\\\ &= p\_j - y\_j \end{aligned} $$

Useful resources