Docs
AI
DL
Parallelism
Parallelism and Vectorization

Parallelism and Vectorization

Vectorization

Consider a single layer in MLP:

x_1
\sum
x_1
x_1
x_0
\sigma
z_j
y_j
w_{0j}
w_{1j}
w_{2j}
w_{nj}Viewer does not support full SVG 1.1

$$ \begin{aligned} y\_j &= \sum\_{i=0}^{n} w\_{ij}x\_i \\\\ z\_j &= \sigma(y\_j) = \frac{1}{1 + e^{-x}} \end{aligned} $$

Naive implementation:

  1. Loop over $w\_{ij}$ and $x\_i$, build products
  2. Then compute sigmoid over $y\_j$
for j in range(m):
  for i in range(n):
    y_j += w_ij * x_i 
  z_j = sigmoid(y_j)

“for-loop” over all values is slow

  • Lots of “jmp“s
  • Caching unclear

Modern CPUs have support for SIMD operations

  • vector operations are faster than looping over individual elements

  • In the example above, actually we are just computing

    $$ y=\sigma\left(W \vec{x}^{T}\right) $$
    • $W \in \mathbb{R}^{n \times m}$
    • $x \in \mathbb{R}^{n}$
    • $y \in \mathbb{R}^{m}$

  • Using vectorized hardware instructions is much faster 💪

Parallelism

Is there even more to get?

$$ \begin{array}{c} y=W \vec{x}^{T} \\\\ \\\\ \left(\begin{array}{c} y_{1} \\\\ y_{2} \\\\ \vdots \\\\ y_{m} \end{array}\right)=\left(\begin{array}{c} \color{red}{w_{01} x_{0}+\cdots+w_{n 1} x_{n}} \\\\ \color{orange}{w_{02} x_{0}+\cdots+w_{n 2} x_{n}} \\\\ \vdots \\\\ \color{green}{w_{0 m} x_{0}+\cdots+w_{n m} x_{n}} \end{array}\right) \end{array} $$

Computation of independent results in parallel! 💪

Parallelism in CPUs

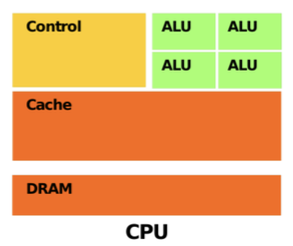
截屏2020-08-20 18.15.26

  • Structure

    • Several Compute Cores (ALUs)
    • Complex control logic
    • Large Caches (L1 / L2, …)
    • Optimized for serial operations like regular program flow
    • shallow pipelines
    • Increasingly more cores
    • Parallelizing code will give speedup
    • Libraries exist that do that for us (BLAS…)

  • CPUs were build for (mostly) sequential code

  • Computations in deep learning are extremely deterministic

    • Known sequence of operation
    • No branches no out of order
    • All parallel operations essentially do the same
    • After computing something the same input is rarely used again

    $\to$ Different kind of hardware might be better suited

Parallelism in GPUs

截屏2020-08-20 18.18.58

  • Many Compute Cores (ALUs)
  • Built for parallel operations
  • Deep pipelines (hundreds of stages) High throughput
  • Newer GPUs:
    • More like CPUs
    • Multiway pipelines

Frameworks for Deep Learning

  • Abstraction for access and usage of (GPU) resources
  • Reference implementation for typical components
    • Layers
    • Activation functions
    • Loss Functions
    • Optimization algorithms
    • Common Models
    • …
  • Automatic differentiation

Variants of Deep Learning Frameworks

  • Static Computational Graph

    • Computation graph is created ahead of time
    • Interaction with the computational graph by “executing” the graph on data
    • Errors in the graph will cause problems during creation
    • Hard to debug
    • Flow Control more difficult (especially writing RNNs)

  • Dynamic Graph builders

    • Uses general purpose automatic differentiation operator overloading
    • Models are written like regular programs, including
      • Branching
      • Loops
      • Recursion
      • Procedure calls
    • Errors in Graph will cause problems during “runtime”

Automatic Differentiation

Automatic construction of procedure to compute derivative of computed value

  • Reverse Mode
    • Converting program into a sequence of primitive operations with known derivatives
    • Each element of a computing graph has a rule how to build the gradient
    • During forward pass, intermediate results are stored
    • Backward pass can compute gradients based on rule and stored results
    • => backprop can be done completely mechanical
  • Forward Mode
    • Computed during forward pass in parallel with evaluation