Docs
AI
DL
Unsupervised Learning
Auto Encoder

Auto Encoder

Supervised vs. Unsupervised Learning

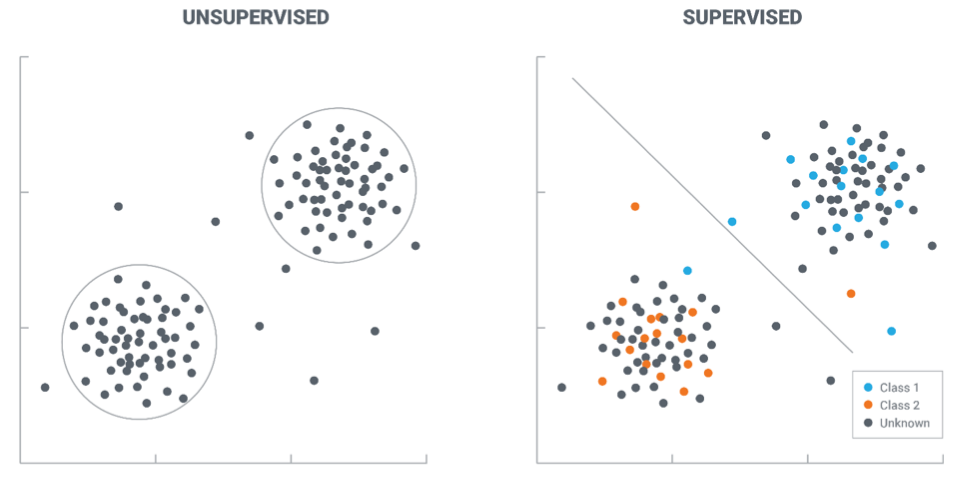
Supervised vs. unsupervised

Supervised vs. unsupervised

  • Supervised learning
    • Given data $(X, Y)$
    • Estimate the posterior $P(Y|X)$
  • Unsupervised learning
    • Concern with the structure (unseen) of the data
    • Try to estimate (implicitly or explicitly) the data distribution $P(X)$

Auto-Encoder structure

In supervised learning, the hidden layers encapsulate the features useful for classification. Even there are no labels or no output layer, it is still possible to learn features in the hidden layer! 💪

Linear auto-encoder

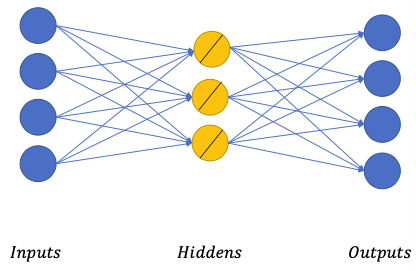
截屏2020-08-17 18.56.10 $$ \begin{array}{l} H=W\_{I} I+b\_{I} \\\\ \tilde{I}=W\_{O} H+b\_{O} \end{array} $$
  • Similar to linear compression method (such as PCA)
  • Trying to find linear surfaces that most data points can lie on
  • Not very useful for complicated data 🤪

Non-linear auto-encoder

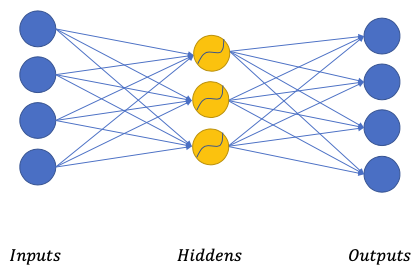
截屏2020-08-17 18.59.24 $$ \begin{array}{l} H=f(W\_{I} I+b\_{I}) \\\\ \tilde{I}=W\_{O} H+b\_{O} \end{array} $$

  • When $D\_H > D\_I$, the activation function also prevents the network to simply copy over the data

  • Goal: find optimized weights to minimize

    $$ L=\frac{1}{2}(\tilde{I}-\mathrm{I})^{2} $$
    • Optimized with Stochastic Gradient Descent (SGD)
    • Gradients computed with Backpropagation

General auto-encoder structure

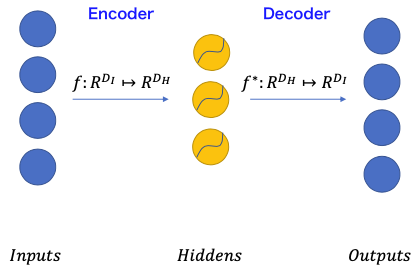
截屏2020-08-17 19.12.15

  • 2 components in general

    • Encoder: maps input $I$ to hidden $H$
    • Decoder: reconstructs $\tilde{I}$ from $H$

    ($f$ and $f^*$ depend on input data type)

  • Encoder and Decoder often have similar/reversed architectures

Why Auto-Encoders?

With auto-encoders we can do

There’re many types and variations of auto-encoders

  • Different architectures for different data types

  • Different loss functions for different learning purposes

Compression and Reconstruction

截屏2020-08-17 18.59.24

  • $D\_H < D\_I$

    • For example a flattened image: $D\_I = 1920 \times 1080 \times 3$
    • Common hidden layer sizes: $512$ or $1024$

    $\to$ Sending $H$ takes less bandwidth then $I$

  • Sender uses $W\_I$ and $b\_I$ to compress $I$ into $H$

  • Receiver uses $W\_O$ and $b\_O$ to reconstruct $\tilde{I}$

With corrupted inputs

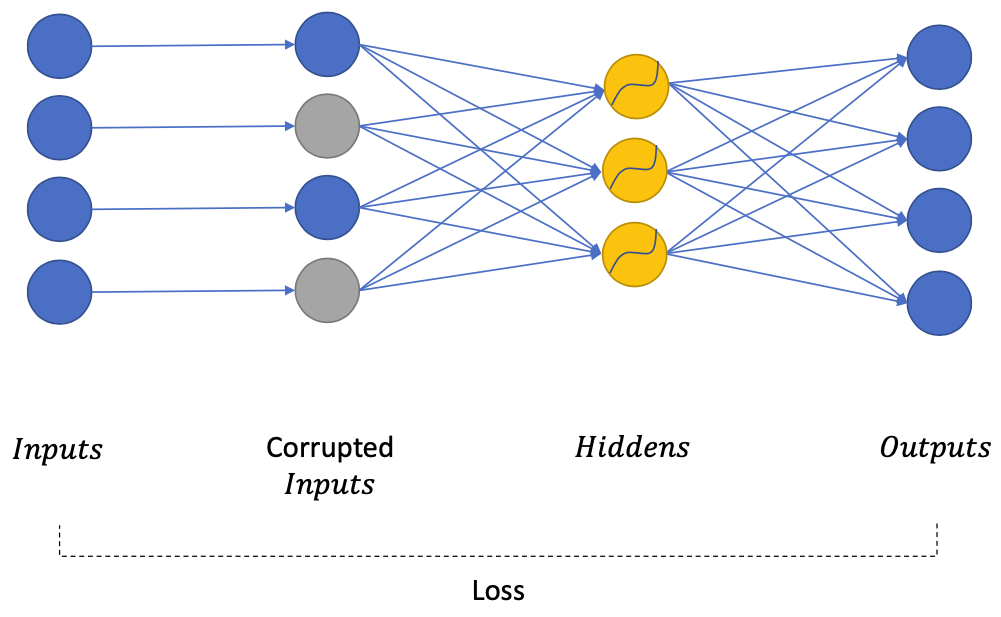
截屏2020-08-17 21.23.56

  • Deliberately corrupt inputs

  • Train auto-encoders to regenerate the inputs before corruption

  • $D\_H < D\_I$ NOT required (no risk of learning an identity function)

  • Benefit from a network with large capacity

  • Different ways of corruption

    • Images
      • Adding noise filters
      • downscaling
      • shifting
      • …
    • Speech
      • simulating background noise
      • Creating high-articulation effect
      • …
    • Text: masking words/characters

  • Application

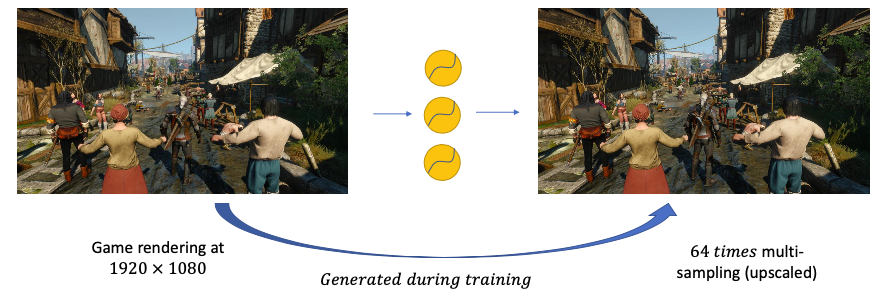
    • Deep Learning super sampling

      • use neural auto-encoders to generate HD frames from SD frames

      截屏2020-08-17 21.30.49

    • Denoising Speech from Microphones

Unsupervised Pretraining

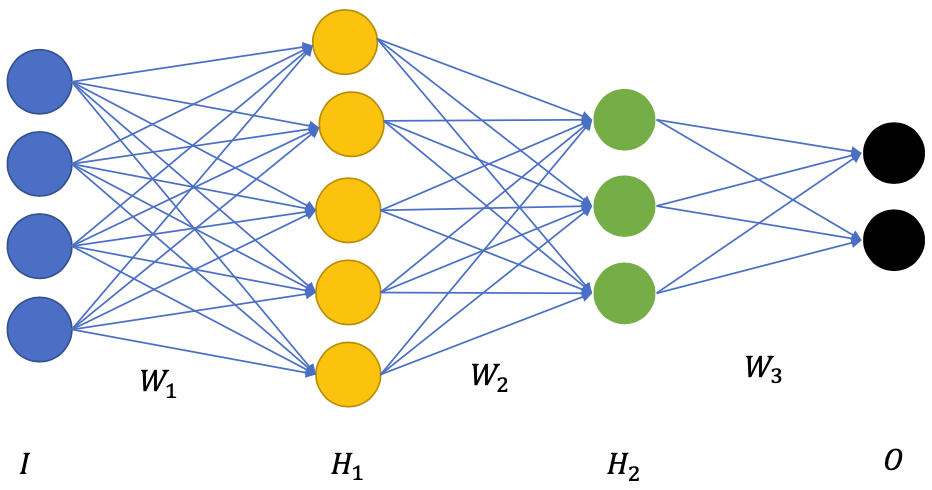
截屏2020-08-17 21.33.04

Normal training regime

  1. Initialize the networks with random $W\_1, W\_2, W\_3$
  2. Forward pass to compute output $O$
  3. Get the loss function $L(O, Y)$
  4. Backward pass and update weights to minimize $L$

Pretraining regime

  • Find a way to have $W\_1, W\_2, W\_3$ pretrained 💪
  • They are used to optimize auxiliary functions before training

Layer-wise pretraining

Pretraining first layer
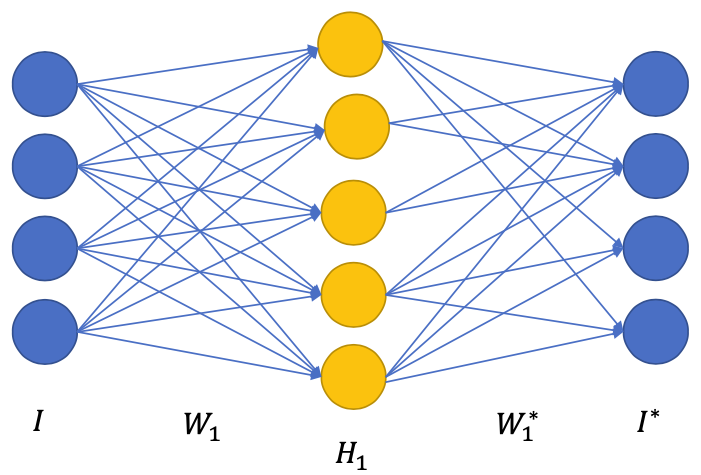
截屏2020-08-17 21.37.12

  1. Initialize $W\_1$ to encode, $W\_1^*$ to decode

  2. Forward pass

    • $I \to H\_1 \to I^*$

    • Reconstruction loss:

      $$ L = \frac{1}{2}(I^* - I)^2 $$

  3. Backward pass

    • Compute gradients $\frac{\delta L}{\delta W_{1}}$ and $\frac{\delta L}{\delta W_{1}^*}$

  4. Update $W\_1$, $W\_1^*$ with SGD

  5. Repeat 1 to 4 until convergence

Pretraining next layers
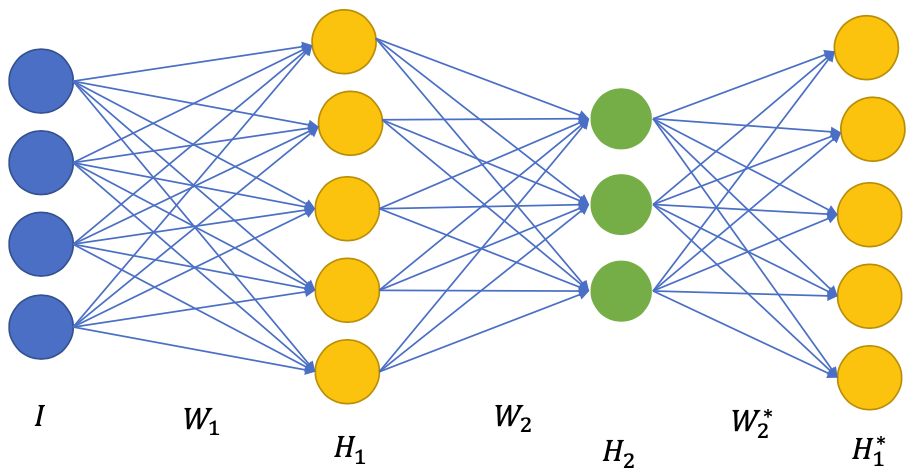
截屏2020-08-17 21.41.39
  • Use $W\_1$ from previous pretraining

  1. Initialize $W\_2$ to encode, $W\_2^*$ to decode

  2. Forward pass

    • $I \to H\_1 \to H\_2 \to I^*$

    • Reconstruction loss:

      $$ L = \frac{1}{2}(H\_1^* - H\_1)^2 $$

  3. Backward pass

    • Compute gradients $\frac{\delta L}{\delta W_{2}}$ and $\frac{\delta L}{\delta W_{2}^*}$

  4. Update $W\_2$, $W\_2^*$ with SGD and keep $W\_1$ the same

Hidden layers pretraining in general
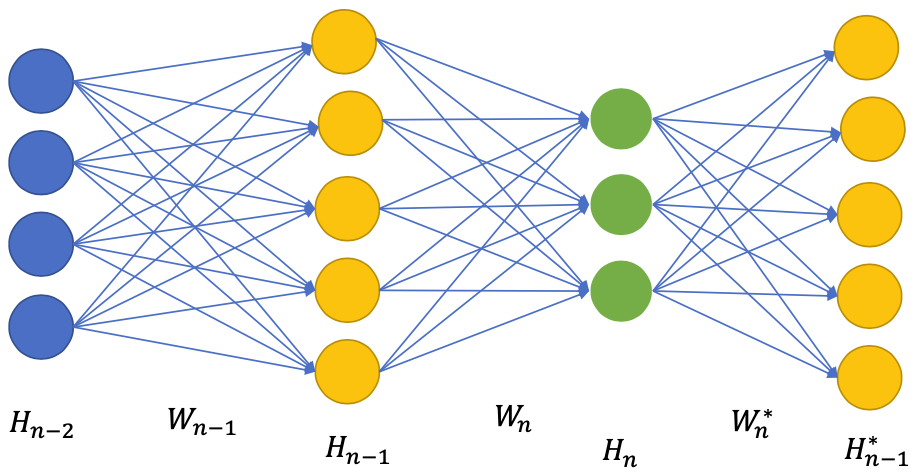
截屏2020-08-17 21.46.02
  • Each layer $H\_n$ is pretrained as an AE to reconstruct the input of that layer (i.e $H\_{n-1}$)
  • The backward pass is stopped at the input to prevent changing previous weights $W\_1, \dots, W\_{n-1}$ and ONLY update $W\_n, W\_n^*$
  • Complexity of each AE increases over depth (since the forward pass requires all previously pretrained layers)
Finetuning
  • Start the networks with pretrained $W\_1, W\_2, W\_3$
  • Go back to supervised training:
    1. Forward pass to compute output $O$
    2. Get the loss function $L(O, Y)$
    3. Backward pass and update weights to minimize $L$

This process is called finetuning because the weights are NOT randomly initialized, but carried over from an external process

What does “unsupervised pretraining” help?

According to Why Does Unsupervised Pre-training Help Deep Learning?

  • Pretraining helps to make networks with 5 hidden layers converge
  • Lower classification error rate
  • Create a better starting point for the non-convex optimization process

Restricted Boltzmann Machine

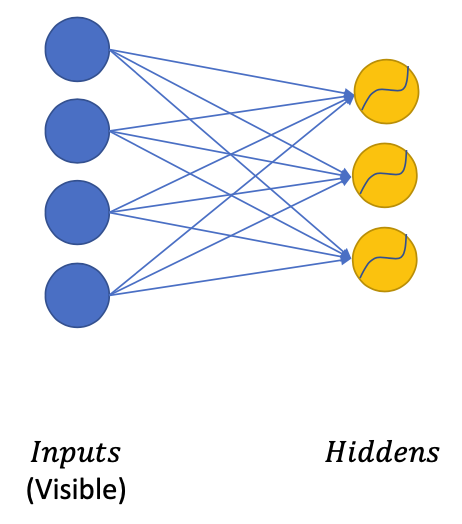
截屏2020-08-17 22.35.40

  • Structure

    • Visible units (Input data points $I$)
    • Hidden units ($H$)

  • Given input $V$, we can generate the probabilities of hidden units being On(1)/Off (0)

    $$ p\left(h\_{j}=1 \mid V\right)=\sigma\left(b\_{j}+\sum\_{i=1}^{m} W\_{i j} v\_{i}\right) $$

  • Given the hidden units, we can generate the probabilities of visible units being On/Off

    $$ p\left(v\_{i} \mid H\right)=\sigma\left(b\_{i}+\sum\_{j=1}^{F} W\_{i j} h\_{j}\right) $$

  • Energy function of a visible-hidden system

    $$ E(V, H)=-\sum\_{i=1}^{m} \sum\_{j=1}^{F} W\_{i j} h\_{j} v\_{i}-\sum\_{i=1}^{m} v\_{i} a\_{i}-\sum\_{j=1}^{F} h\_{j} b\_{j} $$
    • Train the network to minimize the energy function
    • Use Contrastive Divergence algorithm

Layer-wise pretraining with RBM

See also: Restricted Boltzman Machine
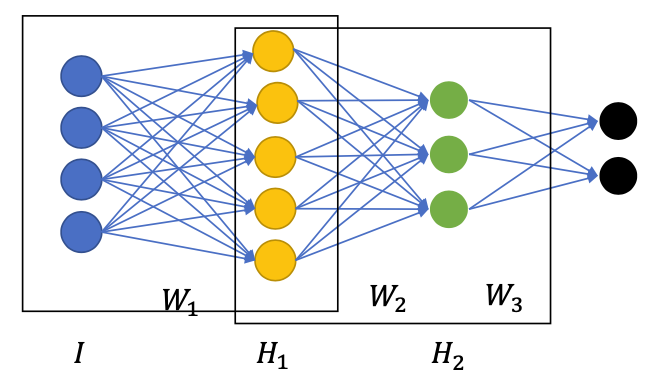
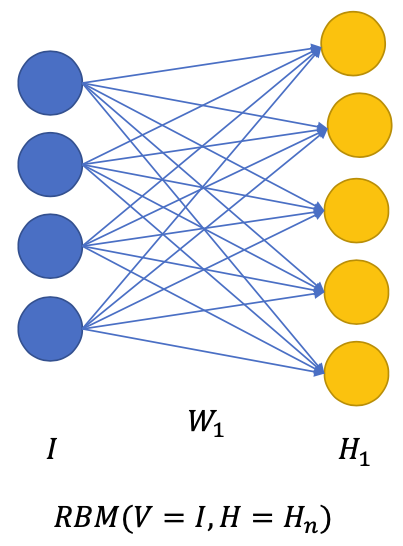
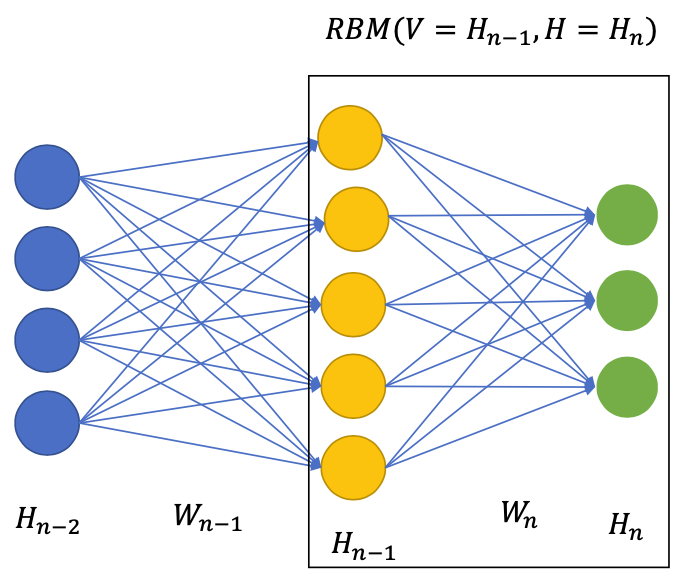
截屏2020-08-17 22.43.06 截屏2020-08-17 22.43.51 截屏2020-08-17 22.44.12

Finetuning RBM: Deep Belief Network

  • The end result is called a Deep Belief Network
  • Use pretrained $W\_1, W\_2, W\_3$ to convert the network into a typical MLP
  • Go back to supervised training:
    1. Forward pass to compute output $O$
    2. Get the loss function $L(O, Y)$
    3. Backward pass and update weights to minimize $L$

RBM Pretraining application in Speech

Speech Recognition = Looking for the most probable transcription given an audio

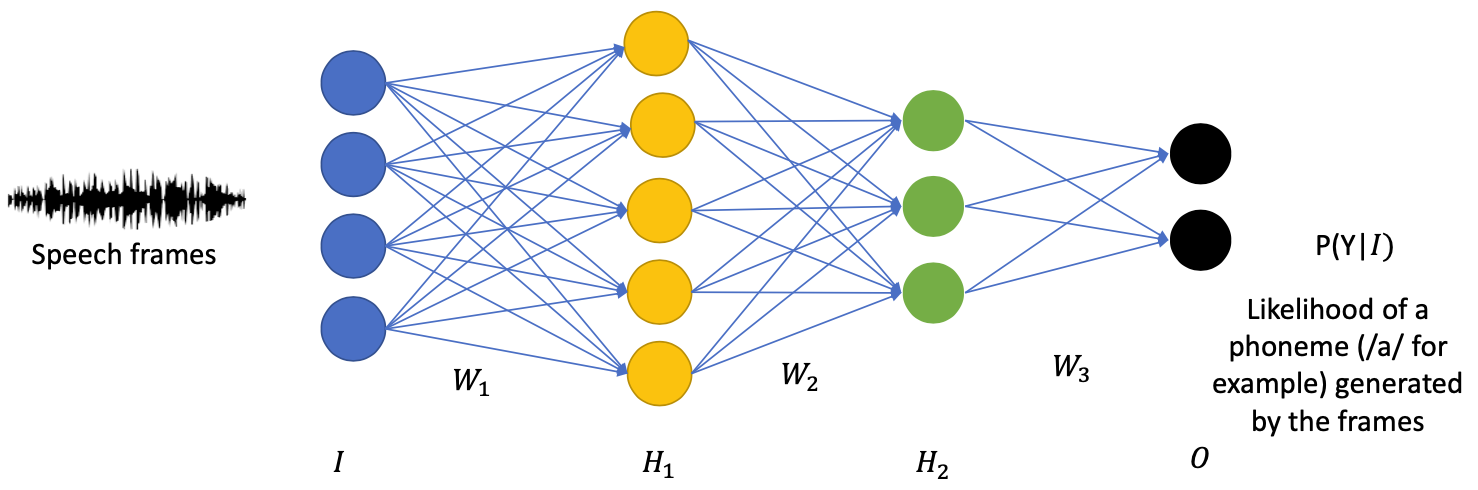
截屏2020-08-17 22.52.35

💡 We can use (deep) neural networks to replace the non-neural generative models (Gaussian Mixture Models) in the Acoustic Models

Variational Auto-Encoder

💡 Main idea:Enforcing the hidden units to follow an Unit Gaussian Distribution (or a known distribution)

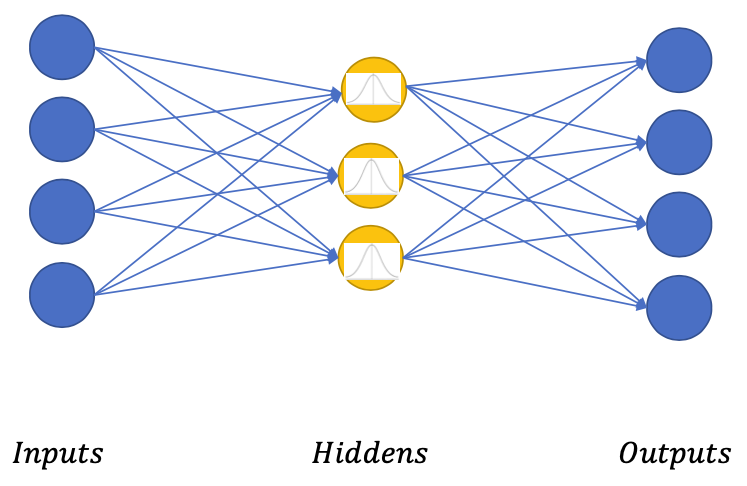
截屏2020-08-17 23.16.51
  • In AE we didn’t know the “distribution” of the (hidden) code
  • Knowing the distribution in advance will make sampling easier
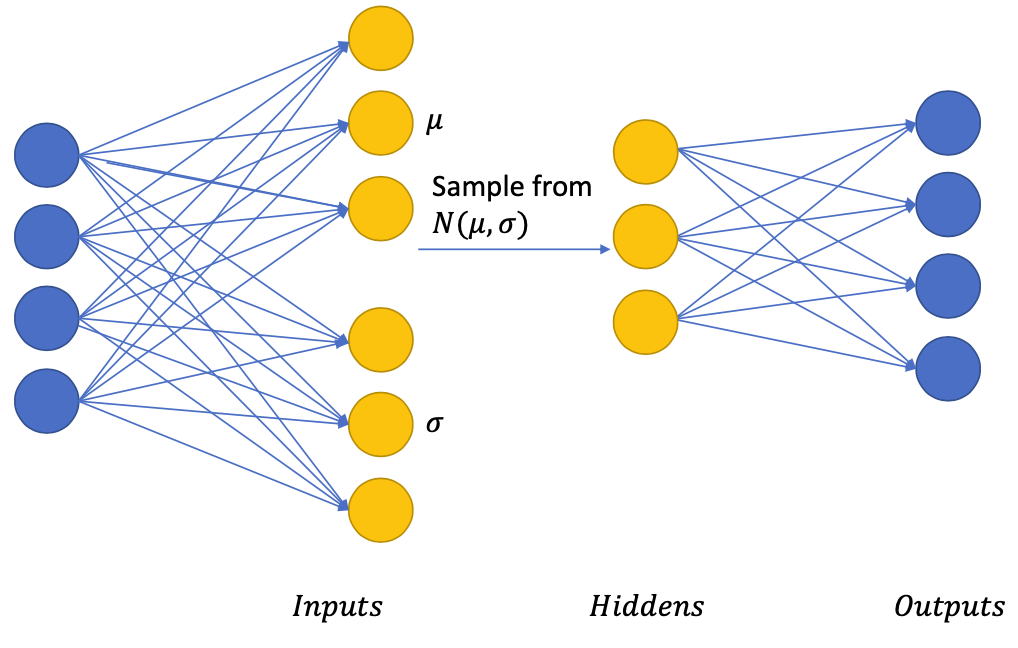
截屏2020-08-17 23.18.50

  • Get the Gaussian restriction

    • Each Gaussian is represented by Mean $𝜇$ and Variance $𝜎$

  • Why do we sample?

    • The hidden layers’ neurons are then “arranged” in the gaussian distribution

  • We wanted to enforce the hidden layers to follow a known distribution, for example $𝑁(0, 𝐼)$, so we can add a loss function to do so:

    $$ L=\frac{1}{2}(O-I)^{2}+\mathrm{KL}(\mathrm{N}(0, I), \mathrm{N}(\mu, \sigma)) $$

  • Variational methods allow us to take a sample of the distribution being estimated, then get a “noisy” gradient for SGD

  • Convergence can be achieved in practice

Structure Prediction

  • Beyond auto-encoder

    • Auto-Encoder
      • Given the object: reconstruct the object
      • $P(X)$ is (implicitly) estimated via reconstructing the inputs
    • Structure prediction
      • Given a part of the object: predict the remaining
      • $P(X)$ is estimated by factorizing the inputs

  • Example

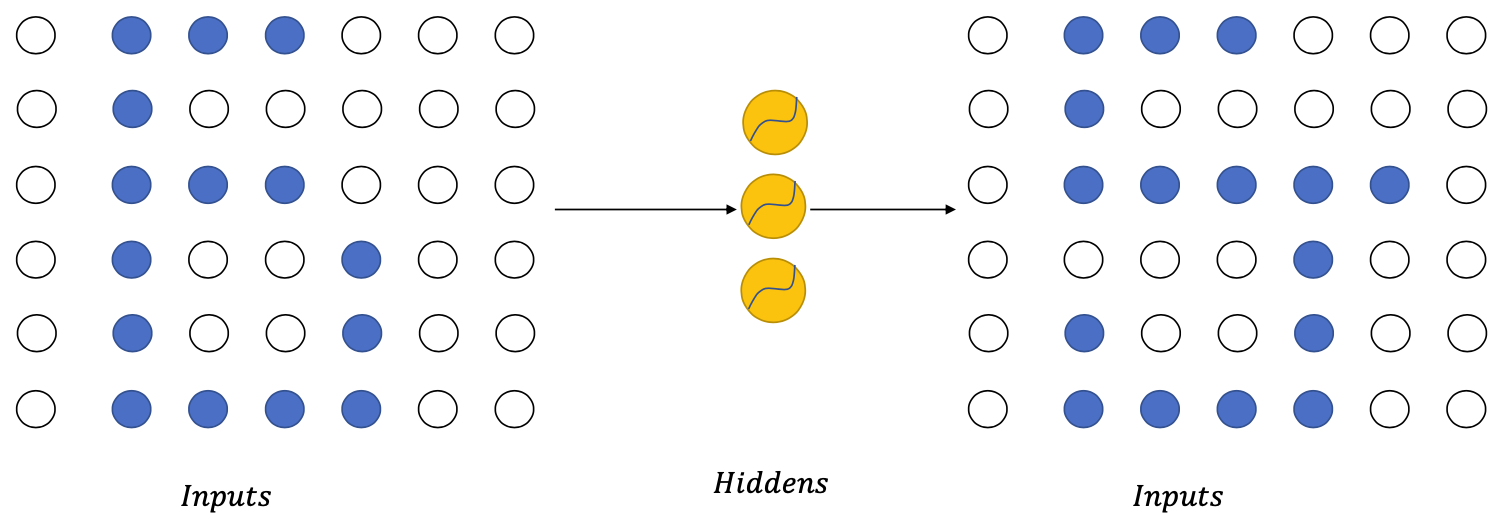
    截屏2020-08-17 23.27.32

Pixel Models

  • Assumption (biased): The pixels are generated from left to right, from top to bottom.

    (I.e. the content of each pixel depends only on the pixels on its left, and its top rows, like image)

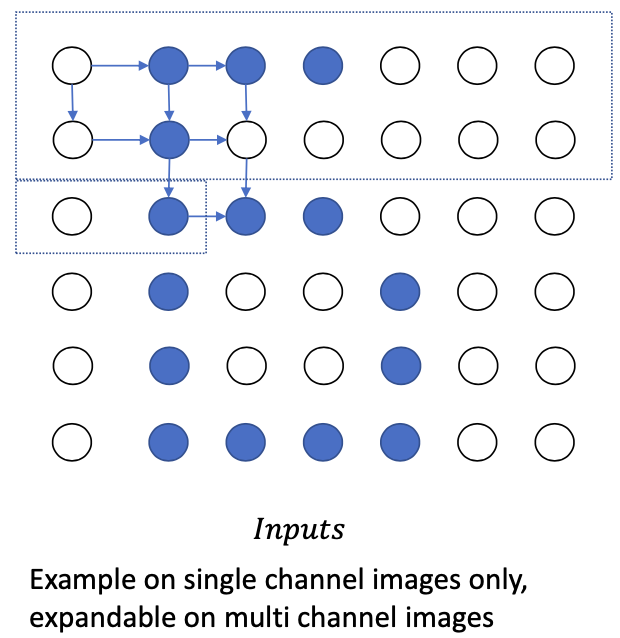
    截屏2020-08-17 23.52.17

  • We can estimate a probabilistic function to learn how to generate pixels

    • Image $X = \\{x\_1, x\_2, \dots, x\_n\\}$ with $n$ pixels $$ P(X)=\prod\_{i=1}^{n} p\left(x\_{i} \mid x\_{1}, \ldots x\_{i-1}\right) $$
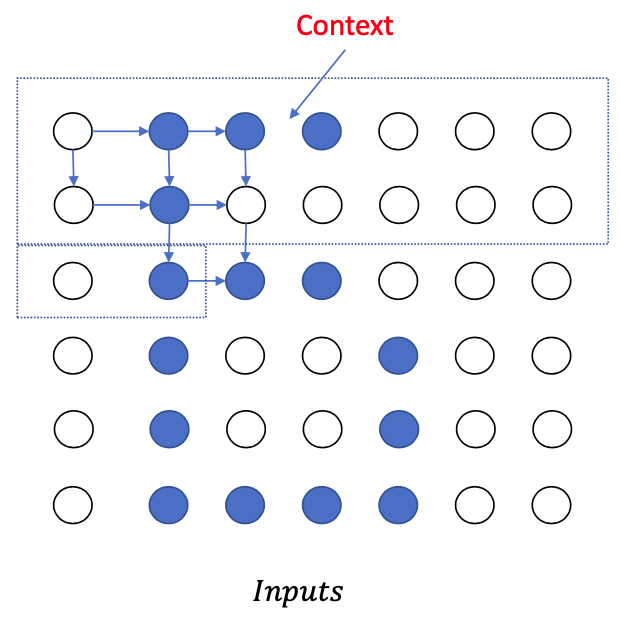
    截屏2020-08-17 23.55.50

    ​ Closer look:

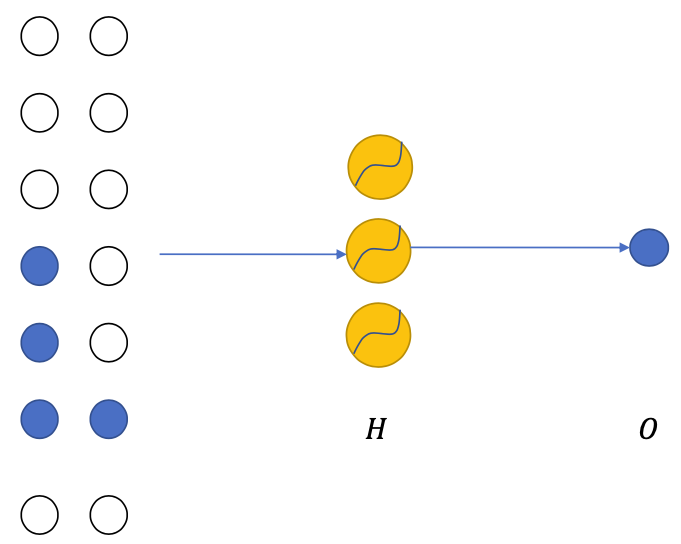
截屏2020-08-17 23.57.43
  • But this is quite difficult
    • The number of input pixels is a variable
    • There are many pixels in an image
  • We can model such context dependency using many types of neural networks:

    • Recurrentneuralnetworks

    • Convolutional neural networks

    • Transformers/Self-attentionNN

(Neural) Language Models

  • A common model/application in natural language processing and generation (E.g. chatbots, translation, question answering)

  • Similar to the pixel models, we can assume the words are generated from left to right

    $$ P( \text{the end of our life} )=P( \text{the} ) \times P( \text{end} \mid {the} ) \times P(\text{of} \mid \text{the end} ) \times P( \text{our} \mid \text{the end of} ) \times P(\text{life} \mid \text{the end of our}) $$

  • Each term can be estimated using neural networks under the form $P(x|context)$ with context being a series of words

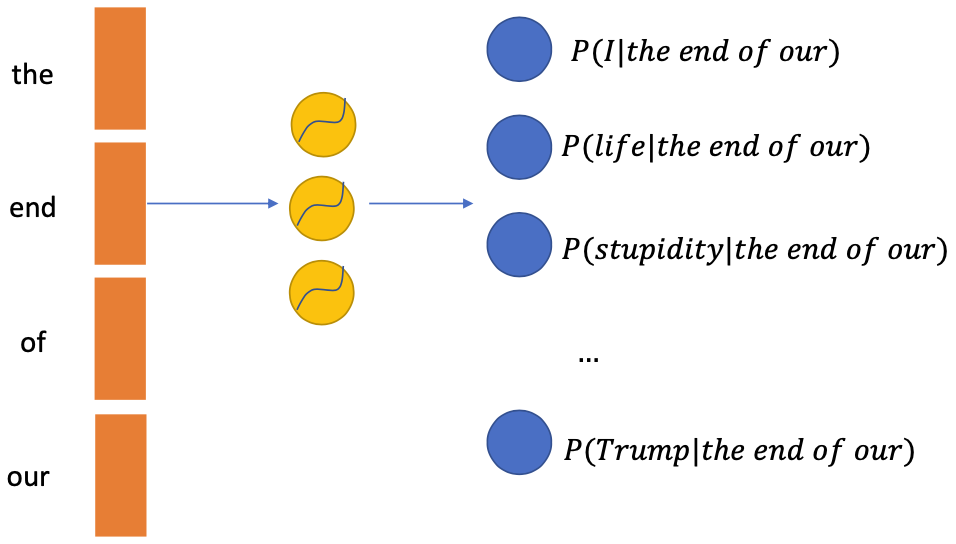
    截屏2020-08-18 00.18.49
    • Input: context
    • Output: classification with $V$ classes (the vocabulary size)
      • Most classes will have near 0 probabilities given the context

Summary

  • Structure prediction is
    • An explicit and flexible method to deal with estimating the likelihood of data that can be factorized (with bias)
    • Motivation to develop a lot of flexible techniques
      • Such as sequence to sequence models, attention models
  • The bias is often the weakness 🤪

Reference