Docs
AI
DL
Unsupervised Learning
Bolzmann Machine

Bolzmann Machine

Boltzmann Machine

  • Stochastic recurrent neural network
  • Introduced by Hinton and Sejnowski
  • Learn internal representations
  • Problem: unconstrained connectivity

Representation

Model can be represented by Graph:

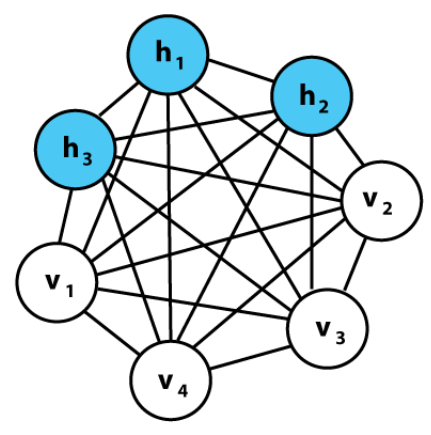
截屏2020-08-18 22.51.29

States

Types:

  • Visible states
    • Represent observed data
    • Can be input/output data
  • Hidden states
    • Latent variable we want to learn
  • Bias states
    • Always one to encode the bias

Binary states

  • unit value $\in \\{0, 1\\}$

Stochastic

  • Decision of whether state is active or not is stochastically

  • Depend on the input

    $$ z\_{i}=b\_{i}+\sum\_{j} s\_{j} w\_{i j} $$
    • $b\_i$: Bias
    • $S\_j$: State $j$
    • $w\_{ij}$: Weight between state $j$ and state $i$
    $$ p\left(s\_{i}=1\right)=\frac{1}{1+e^{-z\_{i}}} $$

Connections

  • Graph can be fully connected (no restrictions)

  • Unidircted:

    $$ w\_{ij} = w\_{ji} $$

  • No self connections:

    $$ w\_{ii} = 0 $$

Energy

Energy of the network

$$ \begin{aligned} E &= -S^TWS - b^TS \\\\ &= -\sum\_{i Probability of input vector $v$

$$ p(v)= \frac{e^{-E(v)}}{\displaystyle \sum\_{u} e^{-E(u)}} $$

Updating the nodes

  • decrease the Energy of the network in average

  • reach Local Minimum (Equilibrium)

  • Stochastic process will avoid local minima

    $$ \begin{array}{c} p\left(s\_{i}=1\right)=\frac{1}{1+e^{-z\_{i}}} \\\\ z\_{i}=\Delta E\_{i}=E\_{i=0}-E\_{i=1} \end{array} $$

Simulated Annealing

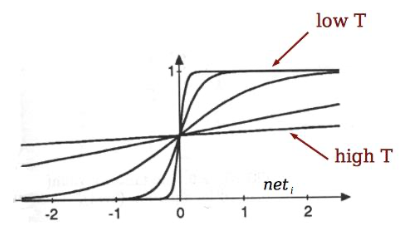
截屏2020-08-18 23.53.50

Use Temperature to allow for more changes in the beginning

  • Start with high temperature

  • “anneal” by slowing lowering T

  • Can escape from local minima 👏

Search Problem

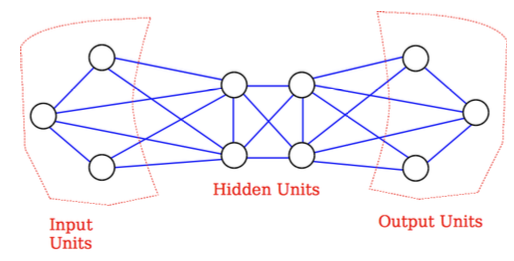
截屏2020-08-18 23.54.58

  • Input is set and fixed (clamped)

  • Annealing is done

  • Answer is presented at the output

  • Hidden units add extra representational power

Learning problem

  • Situations

    • Present data vectors to the network

  • Problem

    • Learn weights that generate these data with high probability

  • Approach

    • Perform small updates on the weights
    • Each time perform search problem

Pros & Cons

✅ Pros

  • Boltzmann machine with enough hidden units can compute any function

⛔️ Cons

  • Training is very slow and computational expensive 😢

Restricted Boltzmann Machine

See also: Restricted Boltzman Machine
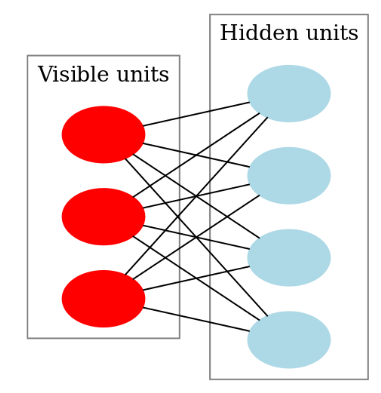
截屏2020-08-18 23.58.36

  • Boltzmann machine with restriction

  • Graph must be bipartite

    • Set of visible units

    • Set of hidden units

  • ✅ Advantage

    • No connection between hidden units
    • Efficient training

Energy

img

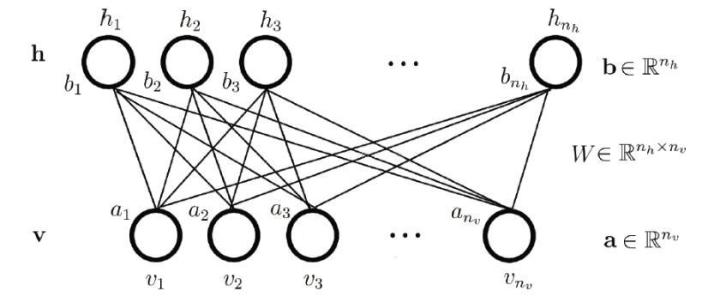
Energy:

$$ \begin{aligned} E(v, h) &= -a^{\mathrm{T}} v-b^{\mathrm{T}} h-v^{\mathrm{T}} W h \\\\ &= -\sum\_{i} a\_{i} v\_{i}-\sum\_{j} b\_{j} h\_{j}-\sum_{i} \sum_{j} v_{i} w_{i j} h_{j} \end{aligned} $$

Probability of hidden unit:

$$ p\left(h\_{j}=1 \mid V\right)=\sigma\left(b\_{j}+\sum\_{i=1}^{m} W\_{i j} v\_{i}\right) $$

Probability of input vector:

$$ p\left(v\_{i} \mid H\right)=\sigma\left(a\_{i}+\sum\_{j=1}^{F} W\_{i j} h\_{j}\right) $$
$$ > \sigma(x)=\frac{1}{1+e^{-x}} > $$

Free Energy:

$$ \begin{array}{l} e^{-F(V)}=\sum\_{j=1}^{F} e^{-E(v, h)} \\\\ F(v)=-\sum\_{i=1}^{m} v\_{i} a\_{i}-\sum_{j=1}^{F} \log \left(1+e^{z_{j}}\right) \\\\ z_{j}=b\_{j}+\sum\_{i=1}^{m} W\_{i j} v\_{i} \end{array} $$