SVM: Basics

🎯 Goal of SVM

To find the optimal separating hyperplane which maximizes the margin of the training data

• it correctly classifies the training data
• it is the one which will generalize better with unseen data (as far as possible from data points from each category)

SVM math formulation

Assuming data is linear separable

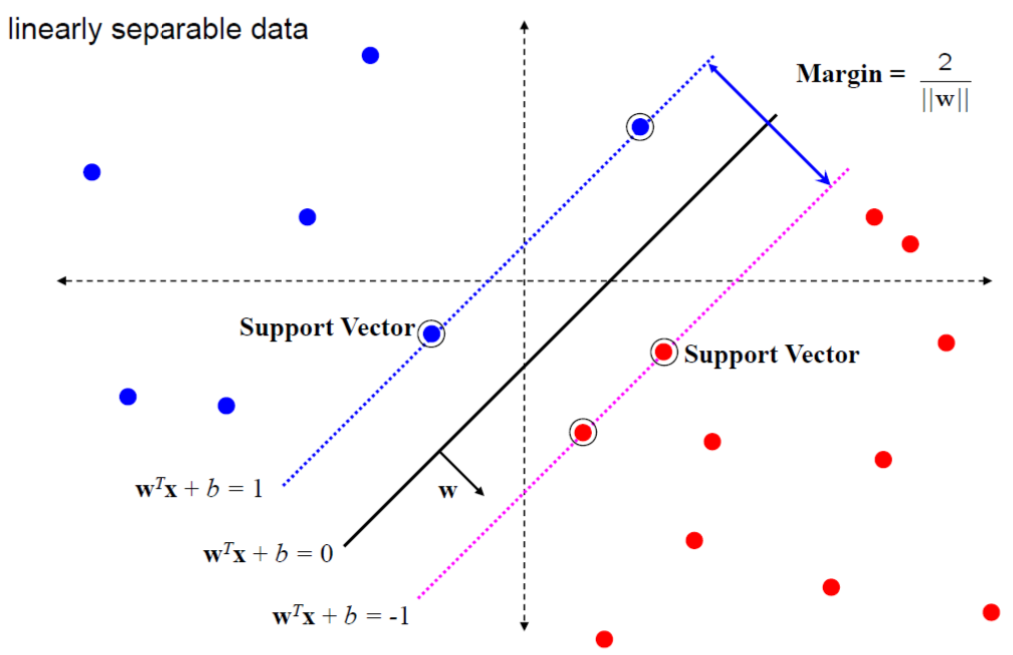
• Decision boundary: Hyperplane $\mathbf{w}^{T} \mathbf{x}+b=0$

• Support Vectors: Data points closes to the decision boundary (Other examples can be ignored)

  • Positive support vectors: $\mathbf{w}^{T} \mathbf{x}_{+}+b=+1$
  • negative support vectors: $\mathbf{w}^{T} \mathbf{x}_{-}+b=-1$

  Why do we use 1 and -1 as class labels?

  • This makes the math manageable, because -1 and 1 are only different by the sign. We can write a single equation to describe the margin or how close a data point is to our separating hyperplane and not have to worry if the data is in the -1 or +1 class.
  • If a point is far away from the separating plane on the positive side, then $w^Tx+b$ will be a large positive number, and $label*(w^Tx+b)$ will give us a large number. If it’s far from the negative side and has a negative label, $label*(w^Tx+b)$ will also give us a large positive number.

• Margin $\rho$ : distance between the support vectors and the decision boundary and should be maximized

  $$\rho = \frac{\mathbf{w}^{T} \mathbf{x}\_{+}+b}{\|\mathbf{w}\|}-\frac{\mathbf{w}^{T} \mathbf{x}\_{-}+b}{\|\mathbf{w}\|}=\frac{2}{\|\mathbf{w}\|}$$

SVM optimization problem

Requirement:

1. Maximal margin
2. Correct classification

Based on these requirements, we have:

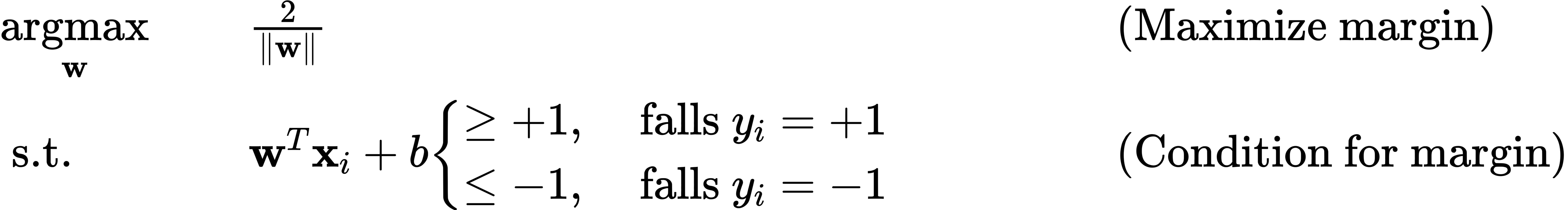
Reformulation:

This is the hard margin SVM.

Soft margin SVM

💡 Idea

“Allow the classifier to make some mistakes” (Soft margin)

➡️ Trade-off between margin and classification accuracy

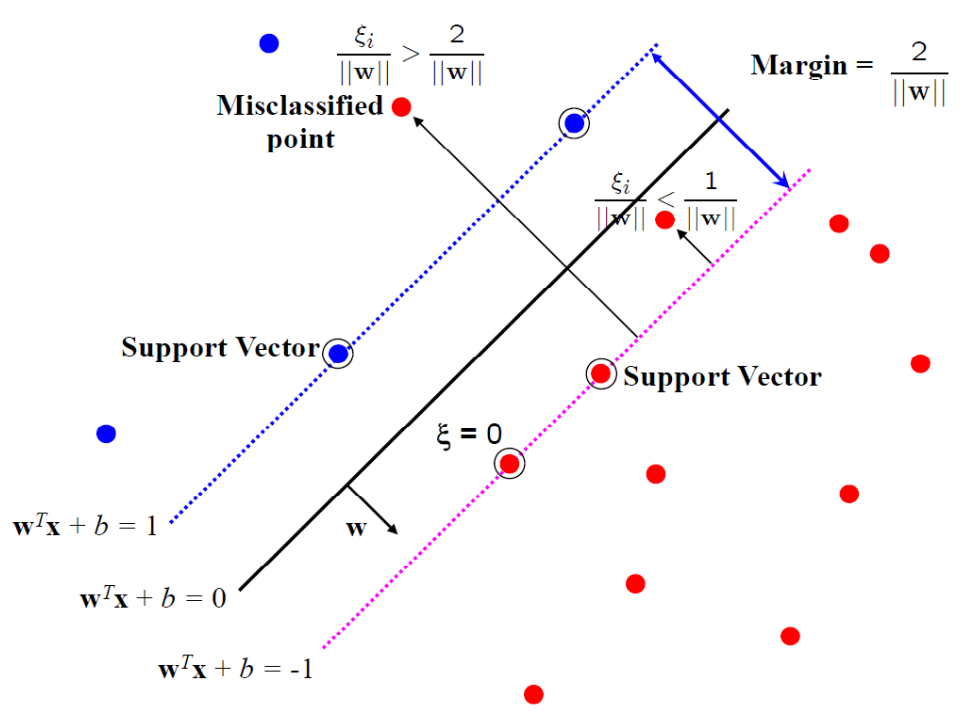
• Slack-variables: ${\color {blue}{\xi_{i}}} \geq 0$

• 💡Allows violating the margin conditions

  $$y_{i}\left(\mathbf{w}^{T} \mathbf{x}_{i}+b\right) \geq 1- \color{blue}{\xi_{i}}$$
  • $0 \leq \xi\_{i} \leq 1$ : sample is between margin and decision boundary (margin violation)
  • $\xi\_{i} \geq 1$ : sample is on the wrong side of the decision boundary (misclassified)

Soft Max-Margin

Optimization problem

• $C$ : regularization parameter, determines how important $\xi$ should be
  • Small $C$: Constraints have little influence ➡️ large margin
  • Large $C$: Constraints have large influence ➡️ small margin
  • $C$ infinite: Constraints are enforced ➡️ hard margin

Soft SVM Optimization

Reformulate into an unconstrained optimization problem

1. Rewrite constraints: $\xi_{i} \geq 1-y_{i}\left(\mathbf{w}^{T} \mathbf{x}_{i}+b\right)=1-y_{i} f\left(\boldsymbol{x}_{i}\right)$
2. Together with $\xi_{i} \geq 0 \Rightarrow \xi_{i}=\max \left(0,1-y_{i} f\left(\boldsymbol{x}_{i}\right)\right)$

Unconstrained optimization (over $\mathbf{w}$):

Points are in 3 categories:

• $y\_{i} f\left(\boldsymbol{x}\_{i}\right) > 1$ : Point outside margin, no contribution to loss

• $y\_{i} f\left(\boldsymbol{x}\_{i}\right) = 1$: Point is on the margin, no contribution to loss as in hard margin

• $y\_{i} f\left(\boldsymbol{x}\_{i}\right) < 1$: Point violates the margin, contributes to loss

Loss function

SVMs uses “hinge” loss (approximation of 0-1 loss)

Hinge loss

For an intended output $t=\pm 1$ and a classifier score $y$, the hinge loss of the prediction $y$ is defined as

$$> \ell(y)=\max (0,1-t \cdot y) >$$

Note that $y$ should be the “raw” output of the classifier’s decision function, not the predicted class label. For instance, in linear SVMs, $y = \mathbf{w}\cdot \mathbf{x}+ b$, where $(\mathbf{w},b)$ are the parameters of the hyperplane and $mathbf{x}$ is the input variable(s).

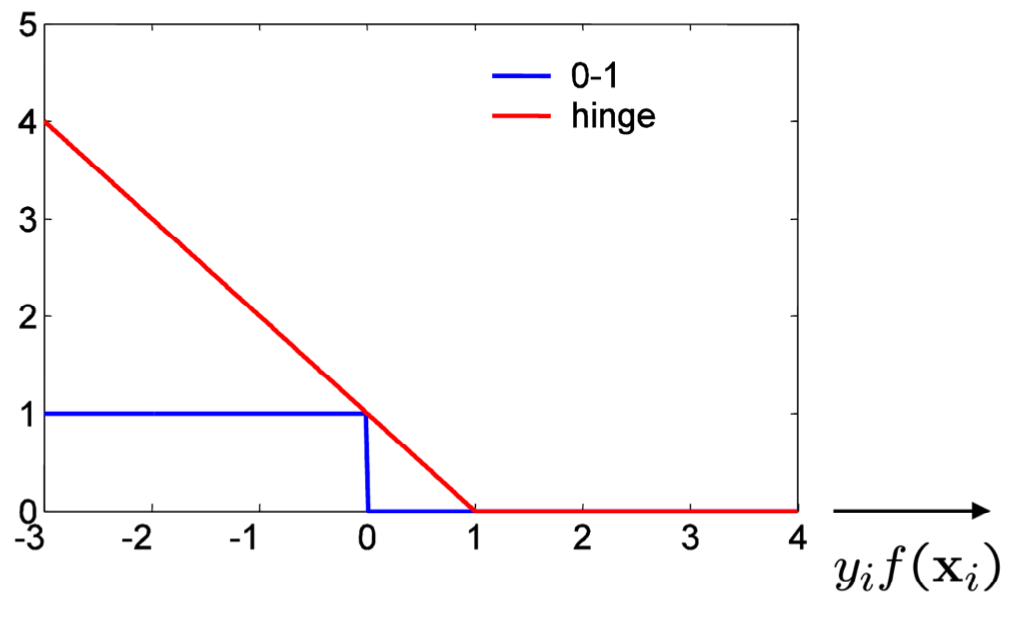
The loss function of SVM is convex:

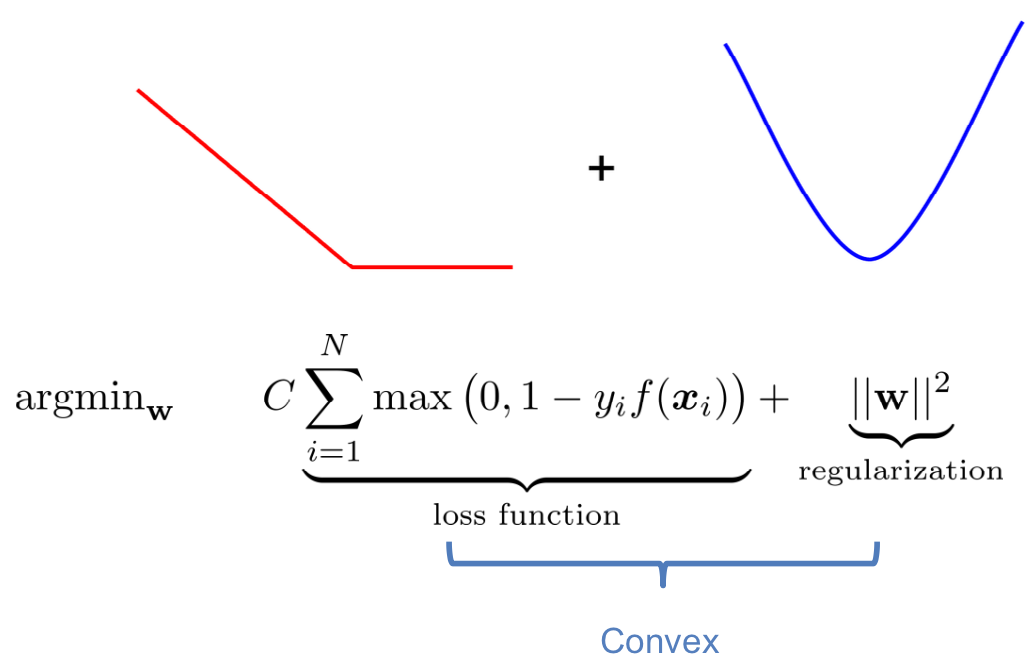
I.e.,

• There is only one minimum
• We can find it with gradient descent
• However: Hinge loss is not differentiable! 🤪

Sub-gradients

For convex function $f: \mathbb{R}^d \to \mathbb{R}$ :

(Linear approximation underestimates function)

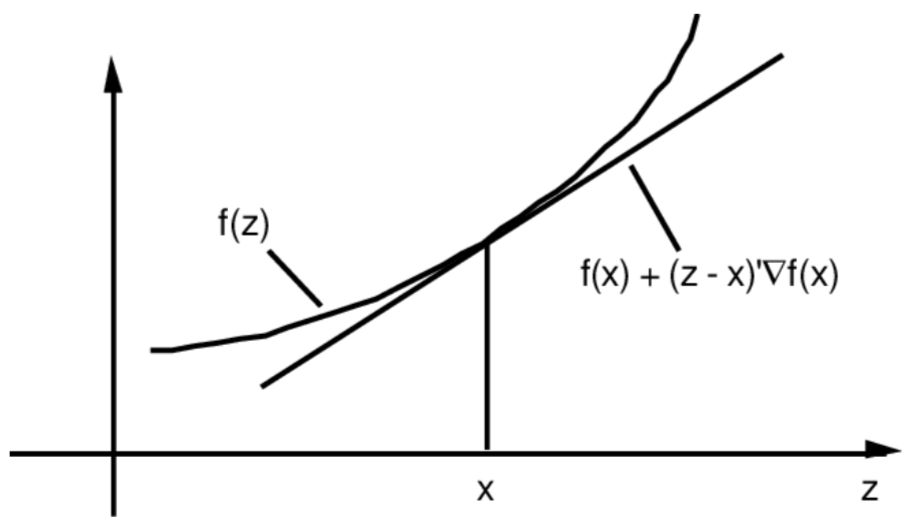
A subgradient of a convex function $f$ at point $\boldsymbol{x}$ is any $\boldsymbol{g}$ such that

• Always exists (even $f$ is not differentiable)
• If $f$ is differentiable at $\boldsymbol{x}$, then: $\boldsymbol{g}=\nabla f(\boldsymbol{x})$

Example

$f(x)=|x|$

• $x \neq 0$ : unique sub-gradient is $g= \operatorname{sign}(x)$
• $x =0$ : $g \in [-1, 1]$

Sub-gradient Method

Sub-gradient Descent

1. Given convex $f$, not necessarily differentiable
2. Initialize $\boldsymbol{x}_0$
3. Repeat: $\boldsymbol{x}\_{t+1}=\boldsymbol{x}\_{t}+\eta \boldsymbol{g}$, where $\boldsymbol{g}$ is any sub-gradient of $f$ at point $\boldsymbol{x}_{t}$

‼️ Notes:

• Sub-gradients do not necessarily decrease $f$ at every step (no real descent method)
• Need to keep track of the best iterate $\boldsymbol{x}^*$

Sub-gradients for hinge loss

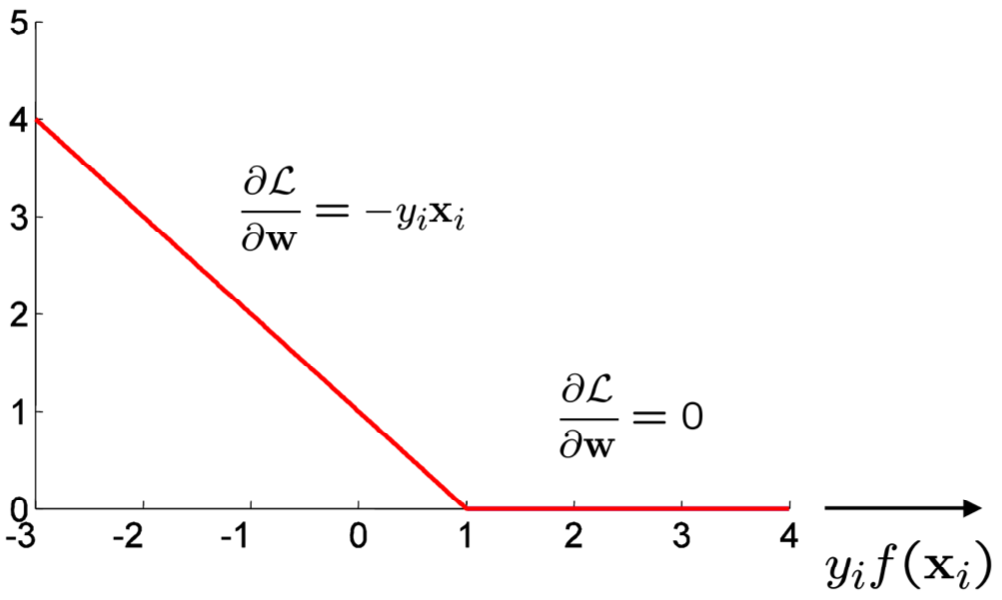
Sub-gradient descent for SVMs

Recall the Unconstrained optimization for SVMs:

At each iteration, pick random training sample $(\boldsymbol{x}_i, y_i)$

• If $y_{i} f\left(\boldsymbol{x}_{i}\right)<1$: ​

  $$\boldsymbol{w}{t+1}=\boldsymbol{w}{t}-\eta\left(2 \boldsymbol{w}{t}-C y{i} \boldsymbol{x}_{i}\right)$$

• Otherwise:

  $$\quad \boldsymbol{w}\_{t+1}=\boldsymbol{w}\_{t}-\eta 2 \boldsymbol{w}\_{t}$$

Application of SVMs

• Pedestrian Tracking
• text (and hypertext) categorization
• image classification
• bioinformatics (Protein classification, cancer classification)
• hand-written character recognition

Yet, in the last 5-8 years, neural networks have outperformed SVMs on most applications.🤪☹️😭