Docs
AI
ML
Decision Trees
CART

Classification And Regression Tree (CART)

Tree-based Methods

CART: Classification And Regression Tree

Grow a binary tree

  • At each node, “split” the data into two “daughter” nodes.
  • Splits are chosen using a splitting criterion.
  • Bottom nodes are “terminal” nodes.
Type of treePredicted value at a nodeSplit criterion
RegressionRegression treeThe predicted value at a node is the average response variable for all observations in the nodeMinimum residual sum of squares
$$\mathrm{RSS}=\sum_{\text {left }}\left(y_{i}-\bar{y}_{L}\right)^{2}+\sum_{\text {right }}\left(y_{i}-\bar{y}_{R}\right)^{2}$$
  • $\bar{y}_L$ / $\bar{y}_R$: average label values in the left / right subtree
    (Split such that variance in subtress is minimized)
    • ClassificationDecision treeThe predicted class is the most common class in the node (majority vote).Minimum entropy in subtrees
    $$\text { score }=N_{L} H\left(p_{\mathrm{L}}\right)+N_{R} H\left(p_{\mathrm{R}}\right)$$
  • $H\left(p_{L}\right)=-\sum_{k} p_{L}(k) \log p_{L}(k)$: entropy in the left sub-tree
  • $p_L(k)$: proportion of class $k$ in left tree
    (Split such that class-labels in sub-trees are “pure”)

    • When stop?

    Stop if:

    • Minimum number of samples per node
    • Maximum depth

    … has been reached

    (Both criterias again influence the complexity of the tree)

    Controlling the tree complexity

    Number of samples per leafAffect
    SmallTree is very sensitive to noise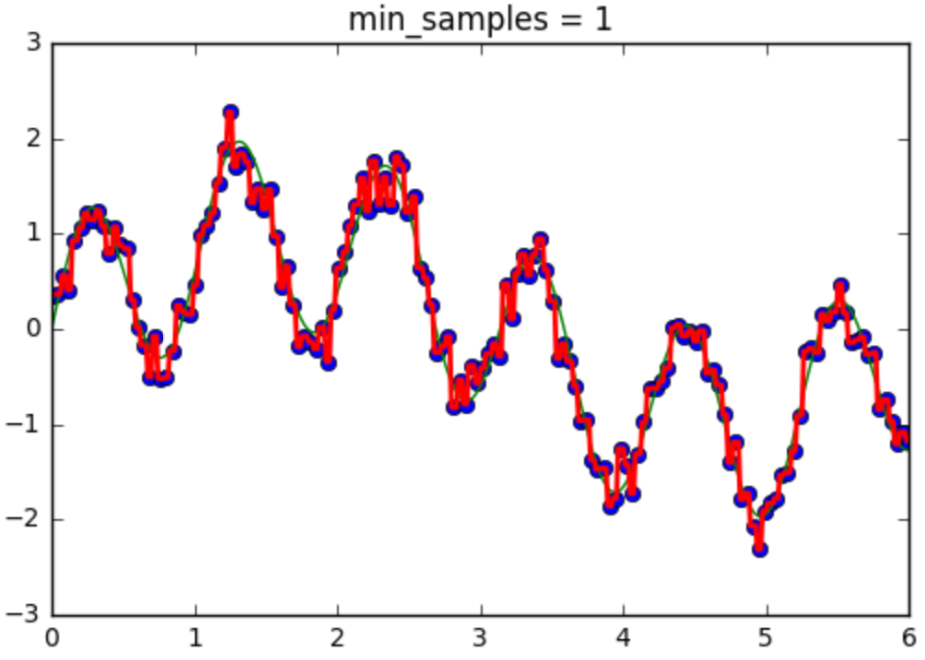屏幕快照 2020-03-01 23.26.23
    屏幕快照 2020-03-01 23.25.40.png
    LargeTree is not expressive enough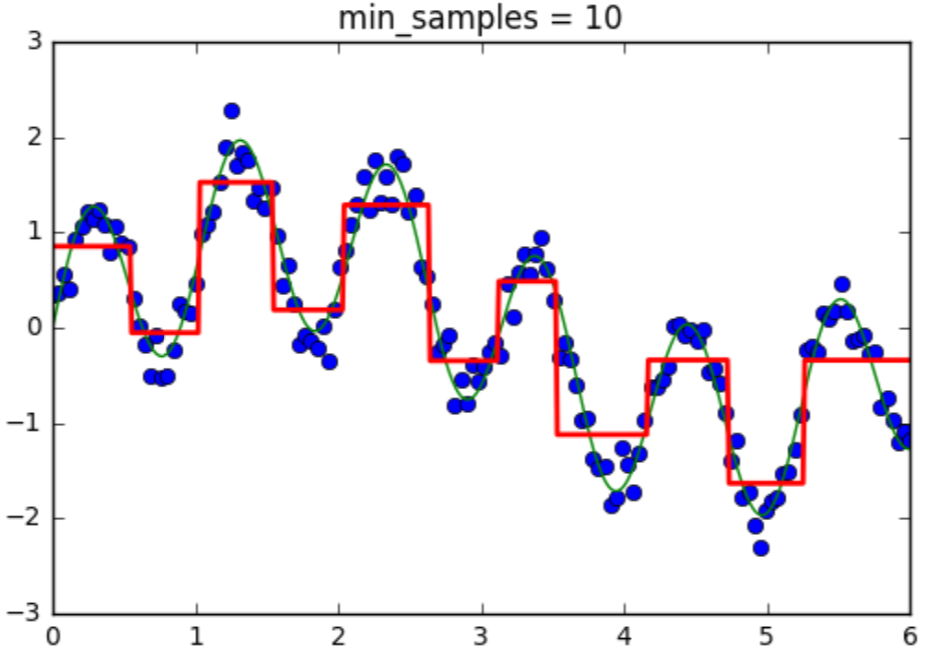屏幕快照 2020-03-01 23.25.50

    Advantages 👍

    • Applicable to both regression and classification problems.

    • Handle categorical predictors naturally.

    • Computationally simple and quick to fit, even for large problems.

    • No formal distributional assumptions (non-parametric).

    • Can handle highly non-linear interactions and classification boundaries.

    • Automatic variable selection.

    • Very easy to interpret if the tree is small.

    Disadvantages 👎

    • Accuracy

      current methods, such as support vector machines and ensemble classifiers often have 30% lower error rates than CART.

    • Instability

      if we change the data a little, the tree picture can change a lot. So the interpretation is not as straightforward as it appears.