Docs
AI
ML
Ensemble Learning
Bagging and Pasting

Bagging and Pasting

TL;DR

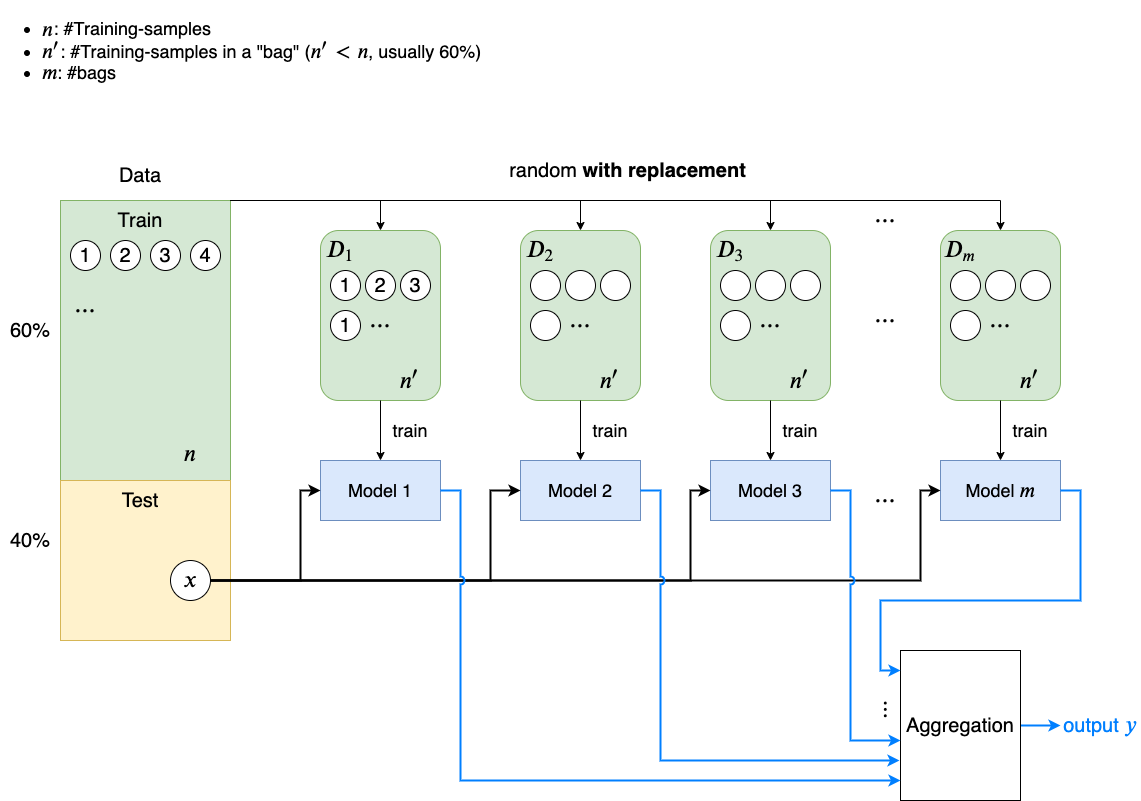
  • Bootstrap Aggregating (Boosting): Sampling with replacement

    Boostrap_Aggregating

  • Pasting: Sampling without replacement

Explaination

Ensemble methods work best when the predictors are as independent from one another as possible.

One way to get a diverse set of classifiers: use the same training algorithm for every predictor, but to train them on different random subsets of the training set

  • Sampling with replacement: boostrap aggregating (Bagging)
  • Sampling without replacement: pasting

Once all predictors are trained, the ensemble can make a prediction for a new instance by simply aggregating the predictions of all predictors. The aggregation function is typically the statistical mode

  • classification: the most frequent prediction (just like a hard voting classifier)
  • regression: average

Each individual predictor has a higher bias than if it were trained on the original training set, but aggregation reduces both bias and variance. 👏

Generally, the net result is that the ensemble has a similar bias but a lower variance than a single predictor trained on the original training set.

##Advantages of Bagging and Pasting

  • Predictors can all be trained in parallel, via different CPU cores or even different servers.
  • Predictions can be made in parallel.

-> They scale very well 👍

Bagging vs. Pasting

  • Bootstrapping introduces a bit more diversity in the subsets that each predictor is trained on, so bagging ends up with a slightly higher bias than pasting, but this also means that predictors end up being less correlated so the ensemble’s variance is reduced.

  • Overall, bagging often results in better models

  • However, if you have spare time and CPU power you can use cross- validation to evaluate both bagging and pasting and select the one that works best.

Out-of-Bag Evaluation

With bagging, some instances may be sampled several times for any given predictor, while others may not be sampled at all. This means that only about 63% of the training instances are sampled on average for each predictor.

The remaining 37% of the training instances that are not sampled are called out-of-bag (oob) instances. Note that they are not the same 37% for all predictors.

Since a predictor never sees the oob instances during training, it can be evaluated on these instances, without the need for a separate validation set. You can evaluate the ensemble itself by averaging out the oob evaluations of each predictor.