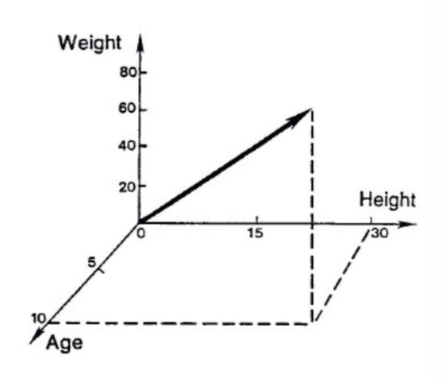
Math Basics
Linear Algebra
Vectors
Vector: multi-dimensional quantity
Each dimension contains different information (e.g.: Age, Weight, Height…)
represented as bold symbols
A vector $\boldsymbol{x}$ is always a column vector
$$ \boldsymbol{x}=\left[\begin{array}{l} {1} \\\\ {2} \\\\ {4} \end{array}\right] $$A transposed vector $\boldsymbol{x}^T$ is a row vector
$$ \boldsymbol{x}^{T}=\left[\begin{array}{lll} {1} & {2} & {4} \end{array}\right] $$
Vector Operations
Multiplication by scalars
$$ 2\left[\begin{array}{l} {1} \\\\ {2} \end{array}\right]=\left[\begin{array}{l} {2} \\\\ {4} \end{array}\right] $$Addtition of vectors
$$ \left[\begin{array}{l}{1} \\\\ {2} \end{array}\right]+\left[\begin{array}{l}{3} \\\\ {1}\end{array}\right]=\left[\begin{array}{l}{4} \\\\ {3} \end{array}\right] $$Scalar (Inner) products: Sum the element-wise products
$$ \boldsymbol{v}=\left[\begin{array}{c}{1} \\\\ {2} \\\\ {4}\end{array}\right], \quad \boldsymbol{w}=\left[\begin{array}{l}{2} \\\\ {4} \\\\ {8}\end{array}\right] $$
- Length of a vector: Square root of the inner product with itself $$ \|\boldsymbol{v}\|=\langle\boldsymbol{v}, \boldsymbol{v}\rangle^{\frac{1}{2}}=\left(1^{2}+2^{2}+4^{2}\right)^{\frac{1}{2}}=\sqrt{21} $$
Matrices
Matrix: rectangular array of numbers arranged in rows and columns
denoted with bold upper-case letters
$$ \boldsymbol{X}=\left[\begin{array}{ll}{1} & {3} \\\\ {2} & {3} \\\\ {4} & {7}\end{array}\right] $$Dimension: $\\#rows \\times \\#columns$ (E.g.: 👆$X \in \mathbb{R}^{3 \times 2}$)
Vectors are special cases of matrices
$$ \boldsymbol{x}^{T}=\underbrace{\left[\begin{array}{ccc}{1} & {2} & {4}\end{array}\right]}_{1 \times 3 \text { matrix }} $$
####Matrices in ML
Data set can be represented as matrix, where single samples are vectors
e.g.:
$$ \text { Joe: } \boldsymbol{x}\_{1}=\left[\begin{array}{c}{37} \\\\ {72} \\\\ {175}\end{array}\right], \qquad \text { Mary: } \boldsymbol{x}\_{2}=\left[\begin{array}{c}{10} \\\\ {30} \\\\ {61}\end{array}\right] \\\\ $$ $$ \text { Carol: } \boldsymbol{x}\_{3}=\left[\begin{array}{c}{25} \\\\ {65} \\\\ {121}\end{array}\right], \qquad \text { Brad: } \boldsymbol{x}\_{4}=\left[\begin{array}{c}{66} \\\\ {67} \\\\ {175}\end{array}\right] $$Age Weight Height Joe 37 72 175 Mary 10 30 61 Carol 25 65 121 Brad 66 67 175 Most typical representation:
- row ~ data sample (e.g. Joe)
- column ~ data entry (e.g. age)
Matrice Operations
Multiplication with scalar
$$ 3 \boldsymbol{M}=3\left[\begin{array}{lll}{3} & {4} & {5} \\\\ {1} & {0} & {1}\end{array}\right]=\left[\begin{array}{ccc}{9} & {12} & {15} \\\\ {3} & {0} & {3}\end{array}\right] $$Addition of matrices
$$ \boldsymbol{M} + \boldsymbol{N}=\left[\begin{array}{lll}{3} & {4} & {5} \\\\ {1} & {0} & {1}\end{array}\right]+\left[\begin{array}{lll}{1} & {2} & {1} \\\\ {3} & {1} & {1}\end{array}\right]=\left[\begin{array}{lll}{4} & {6} & {6} \\\\ {4} & {1} & {2}\end{array}\right] $$Transposed
$$ \boldsymbol{M}=\left[\begin{array}{lll}{3} & {4} & {5} \\\\ {1} & {0} & {1}\end{array}\right], \boldsymbol{M}^{T}=\left[\begin{array}{ll}{3} & {1} \\\\ {4} & {0} \\\\ {5} & {1}\end{array}\right] $$Matrix-Vector product (Vector need to have same dimensionality as number of columns)
$$ \underbrace{\left[\boldsymbol{w}\_{1}, \ldots, \boldsymbol{w}\_{n}\right]}_{\boldsymbol{W}} \underbrace{\left[\begin{array}{c}{v\_{1}} \\\\ {\vdots} \\\\ {v\_{n}}\end{array}\right]}\_{\boldsymbol{v}}=\underbrace{\left[\begin{array}{c}{v\_{1} \boldsymbol{w}\_{1}+\cdots+v\_{n} \boldsymbol{w}\_{n}}\end{array}\right]}\_{\boldsymbol{u}} $$E.g.:
$$ \boldsymbol{u}=\boldsymbol{W} \boldsymbol{v}=\left[\begin{array}{ccc}{3} & {4} & {5} \\\\ {1} & {0} & {1}\end{array}\right]\left[\begin{array}{l}{1} \\\\ {0} \\\\ {2}\end{array}\right]=\left[\begin{array}{l}{3 \cdot 1+4 \cdot 0+5 \cdot 2} \\\\ {1 \cdot 1+0 \cdot 0+1 \cdot 2}\end{array}\right]=\left[\begin{array}{c}{13} \\\\ {3}\end{array}\right] $$💡 Think as: We sum over the columns $\boldsymbol{w}_i$ of $\boldsymbol{W}$ weighted by $v_i$
Matrix-Matrix product
$$ \boldsymbol{U} = \boldsymbol{W} \boldsymbol{V}=\left[\begin{array}{lll}{3} & {4} & {5} \\\\ {1} & {0} & {1}\end{array}\right]\left[\begin{array}{ll}{1} & {0} \\\\ {0} & {3} \\\\ {2} & {4}\end{array}\right]=\left[\begin{array}{ll}{3 \cdot 1+4 \cdot 0+5 \cdot 2} & {3 \cdot 0+4 \cdot 3+5 \cdot 4} \\\\ {1 \cdot 1+0 \cdot 0+1 \cdot 2} & {1 \cdot 0+0 \cdot 3+1 \cdot 4}\end{array}\right]=\left[\begin{array}{cc}{13} & {32} \\\\ {3} & {4}\end{array}\right] $$💡 Think of it as: Each column $\boldsymbol{u}\_i = \boldsymbol{W} \boldsymbol{v}\_i$ can be computed by a matrix-vector product
$$ \boldsymbol{W} \underbrace{\left[\boldsymbol{v}\_{1}, \ldots, \boldsymbol{v}\_{n}\right]}\_{\boldsymbol{V}}=[\underbrace{\boldsymbol{W} \boldsymbol{v}\_{1}}_{\boldsymbol{u}\_{1}}, \ldots, \underbrace{\boldsymbol{W} \boldsymbol{v}\_{n}}\_{\boldsymbol{u}\_{n}}]=\boldsymbol{U} $$Non-commutative: $\boldsymbol{V} \boldsymbol{W} \neq \boldsymbol{W} \boldsymbol{V}$
Associative: $\boldsymbol{V}(\boldsymbol{W} \boldsymbol{X})=(\boldsymbol{V} \boldsymbol{W}) \boldsymbol{X}$
Transpose product:
$$ (\boldsymbol{V} \boldsymbol{W}) ^{T}=\boldsymbol{W}^{T} \boldsymbol{V}^{T} $$
Matrix inverse
scalar
$$ w \cdot w^{-1}=1 $$matrices
$$ \boldsymbol{W} \boldsymbol{W}^{-1}=\boldsymbol{I}, \quad \boldsymbol{W}^{-1} \boldsymbol{W}=\boldsymbol{I} $$
Important Special Cases
Scalar (Inner) product:
$$ \langle\boldsymbol{w}, \boldsymbol{v}\rangle = \boldsymbol{w}^{T} \boldsymbol{v}=\left[w\_{1}, \ldots, w\_{n}\right]\left[\begin{array}{c}{v\_{1}} \\\\ {\vdots} \\\\ {v\_{n}}\end{array}\right]=w\_{1} v\_{1}+\cdots+w\_{n} v\_{n} $$Compute row/column averages of matrix
$$ \boldsymbol{X}=\underbrace{\left[\begin{array}{ccc}{X\_{1,1}} & {\dots} & {X\_{1, m}} \\\\ {\vdots} & {} & {\vdots} \\\\ {X\_{n, 1}} & {\dots} & {X\_{n, m}}\end{array}\right]}\_{n \text { (samples) } \times m \text { (entries) }} $$Vector of row averages (average over all entries per sample)
$$ \left[\begin{array}{cc}{\frac{1}{m} \sum\_{i=1}^{m} X\_{1, i}} \\\\ {\vdots} & {} \\\\ {\frac{1}{m} \sum_{i=1}^{m} X\_{n, i}}\end{array}\right]=\boldsymbol{X}\left[\begin{array}{c}{\frac{1}{m}} \\\\ {\vdots} \\\\ {\frac{1}{m}}\end{array}\right]=\boldsymbol{X} \boldsymbol{a}, \quad \text { with } \boldsymbol{a}=\left[\begin{array}{c}{\frac{1}{m}} \\\\ {\vdots} \\\\ {\frac{1}{m}}\end{array}\right] $$Vector of column averages (average over all samples per entry)
$$ \left[\frac{1}{n} \sum_{i=1}^{n} X\_{i, 1}, \ldots, \frac{1}{n} \sum\_{i=1}^{n} X\_{i, m}\right]=\left[\frac{1}{n}, \ldots, \frac{1}{n}\right] \boldsymbol{X}=\boldsymbol{b}^{T} \boldsymbol{X}, \text { with } \boldsymbol{b}=\left[\begin{array}{c}{\frac{1}{n}} \\\\ {\vdots} \\\\ {\frac{1}{n}}\end{array}\right] $$
Calculus
“The derivative of a function of a real variable measures the sensitivity to change of a quantity (a function value or dependent variable) which is determined by another quantity (the independent variable)”
| Scalar | Vector | |
|---|---|---|
| Function | $f(x)$ | $f(\boldsymbol{x})$ |
| Derivative | $\frac{\partial f(x)}{\partial x}=g$ | $\frac{\partial f(\boldsymbol{x})}{\partial \boldsymbol{x}}=\left[\frac{\partial f(\boldsymbol{x})}{\partial x\_{1}}, \ldots, \frac{\partial f(\boldsymbol{x})}{\partial x\_{d}}\right]^{T} =: \nabla f(x)\quad$ (👆 gradient of function $f$ at $\boldsymbol{x}$) |
| Min/Max | $\frac{\partial f(x)}{\partial x}=0$ | $\frac{\partial f(\boldsymbol{x})}{\partial \boldsymbol{x}}=[0, \ldots, 0]^{T}=\mathbf{0}$ |
Matrix Calculus
| Scalar | Vector | |
|---|---|---|
| Linear | $\frac{\partial a x}{\partial x}=a$ | $\nabla\_{\boldsymbol{x}} \boldsymbol{A} \boldsymbol{x}=\boldsymbol{A}^{T}$ |
| Quadratic | $\frac{\partial x^{2}}{\partial x}=2 x$ | $\begin{array}{l}{\nabla\_{\boldsymbol{x}} \boldsymbol{x}^{T} \boldsymbol{x}=2 \boldsymbol{x}} \\\\ {\nabla\_{\boldsymbol{x}} \boldsymbol{x}^{T} \boldsymbol{A} \boldsymbol{x}=2 \boldsymbol{A} \boldsymbol{x}}\end{array}$ |