Docs
AI
ML
Non-parametric
LDA

Linear Discriminant Analysis (LDA)

Linear Discriminant Analysis (LDA)

  • also called Fisher’s Linear Discriminant

  • reduces dimension (like PCA)

  • but focuses on maximizing seperability among known categories

💡 Idea

  1. Create a new axis
  2. Project the data onto this new axis in a way to maximize the separation of two categories

How it works?

Create a new axis

According to two criteria (considered simultaneously):

  • Maximize the distance between means

  • Minimize the variation $s^2$ (which LDA calls “scatter”) within each category

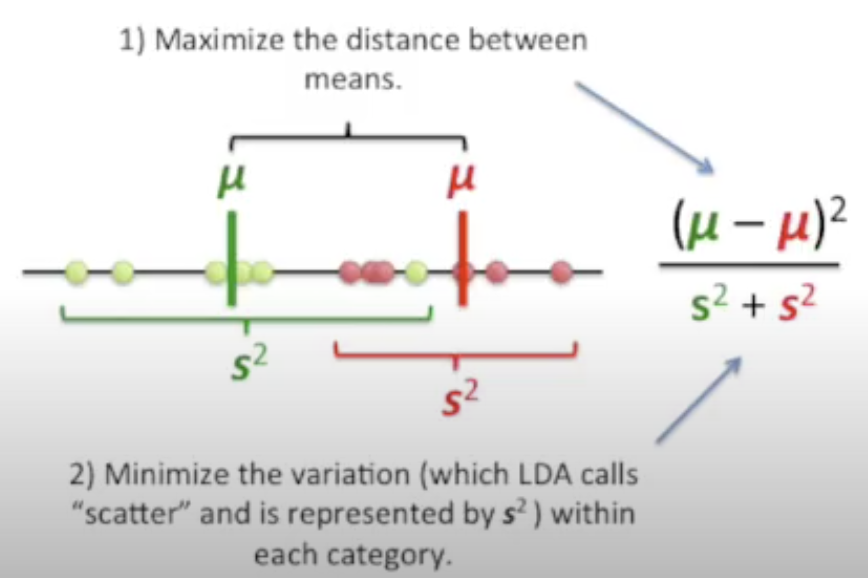
    截屏2020-05-14 15.11.22

We have:

$$ \frac{(\overbrace{\mu_1 - \mu_2}^{=: d})^2}{s_1^2 + s_2^2} \qquad\left(\frac{\text{''ideally large''}}{\text{"ideally small"}}\right) $$

Why both distance and scatter are important?

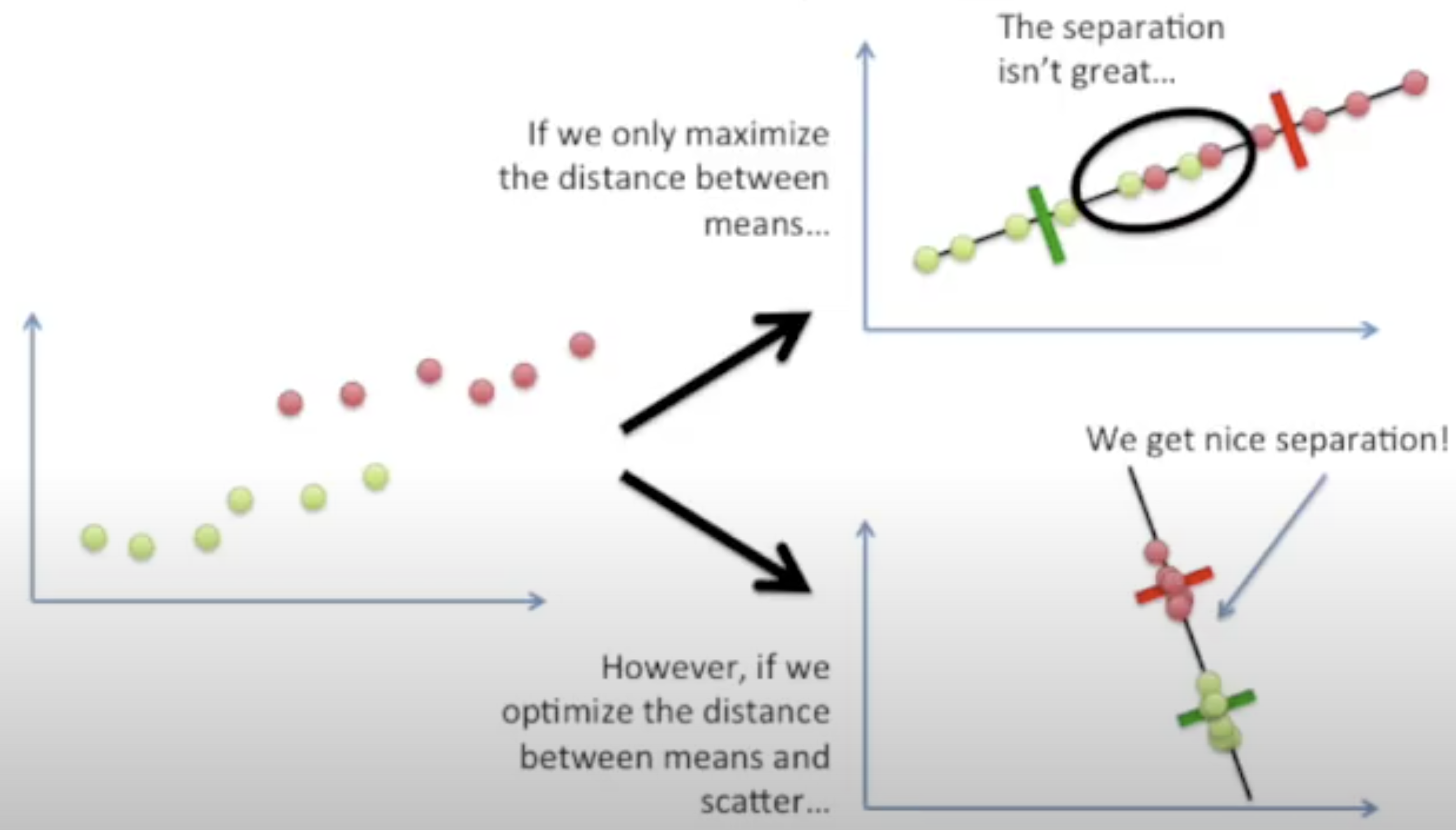
截屏2020-05-14 15.17.59

More than 2 dimensions

The process is the same 👏:

Create an axis that maximizes the distance between the means for the two categories while minimizing the scatter

More than 2 categories (e.g. 3 categories)

Little difference:

  • Measure the distances among the means

    • Find the point that is central to all of the data

    • Then measure the distances between a point that is central in each category and the main central point

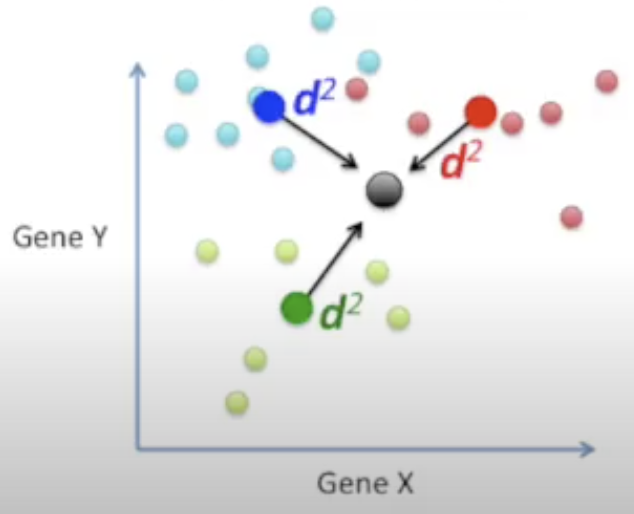
      截屏2020-05-14 15.26.35

    • Maximize the distance between each category and the central point while minimizing the scatter for each category

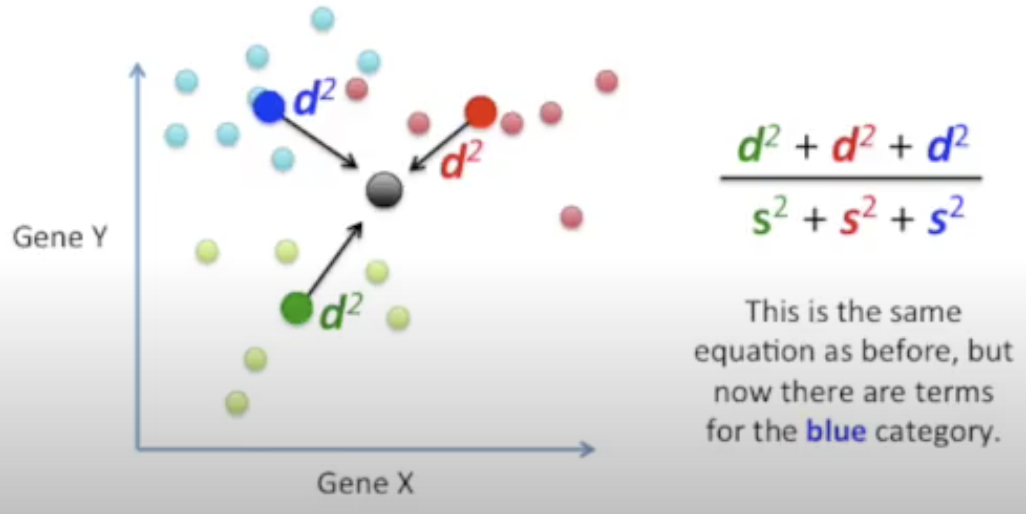
    截屏2020-05-14 15.28.40

  • Create 2 axes to separate the data (because the 3 central points for each category define a plane)

    截屏2020-05-14 15.30.16

LDA and PCA

Similarities

  • Both rank the new axes in order of importance

    • PC1 (the first new axis that PCA creates) accounts for the most variation in the data
      • PC2 (the second new axis) does the second best job
    • LD1 (the first new axis that LDA creates) accounts for the most variation between the categories
      • LD2 does the second best job

  • Both can let you dig in and see which features are driving the new axes

  • Both try to reduce dimensions

    • PCA looks at the features with the most variation
    • LDA tries to maximize the separation of known categories

Reference