Kernelized Ridge Regression
Kernel regression
Kernel identities
Let
$$ \boldsymbol{\Phi}\_{X}=\left[\begin{array}{c} \boldsymbol{\phi}\left(\boldsymbol{x}\_{1}\right)^{T} \\\\ \vdots \\\\ \boldsymbol{\phi}\left(\boldsymbol{x}\_{N}\right)^{T} \end{array}\right] \in \mathbb{R}^{N \times d} , \qquad \left( \boldsymbol{\Phi}\_{X}^T = \left[ \boldsymbol{\phi}(x\_1), \dots, \boldsymbol{\phi}(x\_N)\right] \in \mathbb{R}^{d \times N} \right) $$then the following identities hold:
Kernel matrix
$$ \boldsymbol{K}=\boldsymbol{\Phi}\_{X} \boldsymbol{\Phi}\_{X}^{T} $$with
$$ [\boldsymbol{K}]\_{ij}=\boldsymbol{\phi}\left(\boldsymbol{x}\_{i}\right)^{T} \boldsymbol{\phi}(\boldsymbol{x}\_{j}) = \langle \boldsymbol{\phi}(\boldsymbol{x}\_{i}), \boldsymbol{\phi}(\boldsymbol{x}\_{j}) \rangle = k\left(\boldsymbol{x}\_{i}, \boldsymbol{x}\_{j}\right) $$Kernel vector
$$ \boldsymbol{k}\left(\boldsymbol{x}^{\*}\right)=\left[\begin{array}{c} k\left(\boldsymbol{x}\_{1}, \boldsymbol{x}^{\*}\right) \\\\ \vdots \\\\ k\left(\boldsymbol{x}\_{N}, \boldsymbol{x}^{\*}\right) \end{array}\right]=\left[\begin{array}{c} \boldsymbol{\phi}\left(\boldsymbol{x}\_{1}\right)^{T} \boldsymbol{\phi}(\boldsymbol{x}^{\*}) \\\\ \vdots \\\\ \phi\left(\boldsymbol{x}\_{N}\right)^{T} \boldsymbol{\phi}(\boldsymbol{x}^{\*}) \end{array}\right]=\boldsymbol{\Phi}\_{X} \boldsymbol{\phi}\left(\boldsymbol{x}^{\*}\right) $$
Kernel Ridge Regression
Ridge Regression: (See also: Polynomial Regression (Generalized linear regression models))
- Squared error function + L2 regularization
Linear feature space
Not directly applicable in infinite dimensional feature spaces
Objective:
$$ L_{\text {ridge }}=\underbrace{(\boldsymbol{y}-\boldsymbol{\Phi} \boldsymbol{w})^{T}(\boldsymbol{y}-\boldsymbol{\Phi} \boldsymbol{w})}_{\text {sum of squared errors }}+\lambda \underbrace{\boldsymbol{w}^{T} \boldsymbol{w}}_{L_{2} \text { regularization }} $$- $\boldsymbol{\Phi}\_{X}=\left[\begin{array}{c} \phi\left(\boldsymbol{x}\_{1}\right)^{T} \\\\ \vdots \\\\ \phi\left(\boldsymbol{x}\_{N}\right)^{T} \end{array}\right] \in \mathbb{R}^{N \times d}$
Solution
$$ \boldsymbol{w}\_{\text {ridge }}^{*}= \color{red}{\underbrace{\left(\boldsymbol{\Phi}^{T} \boldsymbol{\Phi}+\lambda \boldsymbol{I}\right)^{-1}}\_{d \times d \text { matrix inversion }}} \boldsymbol{\Phi}^{T} \boldsymbol{y} $$Matrix inversion infeasible in infinite dimensions!!!😭
Apply kernel trick
Rewrite solution as inner products of the feature space with the following matrix identity
$$ (\boldsymbol{I} + \boldsymbol{A}\boldsymbol{B})^{-1}\boldsymbol{A} = \boldsymbol{A} (\boldsymbol{I} + \boldsymbol{B}\boldsymbol{A})^{-1} $$Then we get
$$ \begin{array}{ll} \boldsymbol{w}\_{\text {ridge }}^{*} &= \color{red}{\underbrace{\left(\boldsymbol{\Phi}^{T} \boldsymbol{\Phi}+\lambda \boldsymbol{I}\right)^{-1}}\_{d \times d \text { matrix inversion }}} \boldsymbol{\Phi}^{T} \boldsymbol{y} \\\\ & \overset{}{=} \boldsymbol{\Phi}^{T} \color{LimeGreen}{\underbrace{\left( \boldsymbol{\Phi}\boldsymbol{\Phi}^{T} +\lambda \boldsymbol{I}\right)^{-1}}\_{N \times N \text { matrix inversion }}} \boldsymbol{y} \\\\ &= \boldsymbol{\Phi}^{T} \underbrace{\left( \boldsymbol{K} +\lambda \boldsymbol{I}\right)^{-1}\boldsymbol{y}}_{=: \boldsymbol{\alpha}} \\\\ &= \boldsymbol{\Phi}^{T} \boldsymbol{\alpha} \end{array} $$- beneficial for $d \gg N$
- Still, $\boldsymbol{w}^\* \in \mathbb{R}^d$ is potentially infinite dimensional and can not be represented
Yet, we can still evaluate the function $f$ without the explicit representation of $\boldsymbol{w}^*$ 😉
$$ \begin{array}{ll} f(\boldsymbol{x}) & =\boldsymbol{\phi}(\boldsymbol{x})^{T} \boldsymbol{w}^{*} \\\\ & \overset{}{=}\boldsymbol{\phi}(\boldsymbol{x})^{T} \boldsymbol{\Phi}^{T} \boldsymbol{\alpha} \\\\ & \overset{\text{kernel} \\ \text{trick}}{=}\boldsymbol{k}(\boldsymbol{x})^{T} \boldsymbol{\alpha} \\\\ & =\sum\_{i} \alpha\_{i} k\left(\boldsymbol{x}\_{i}, \boldsymbol{x}\right) \end{array} $$For a Gaussian kernel
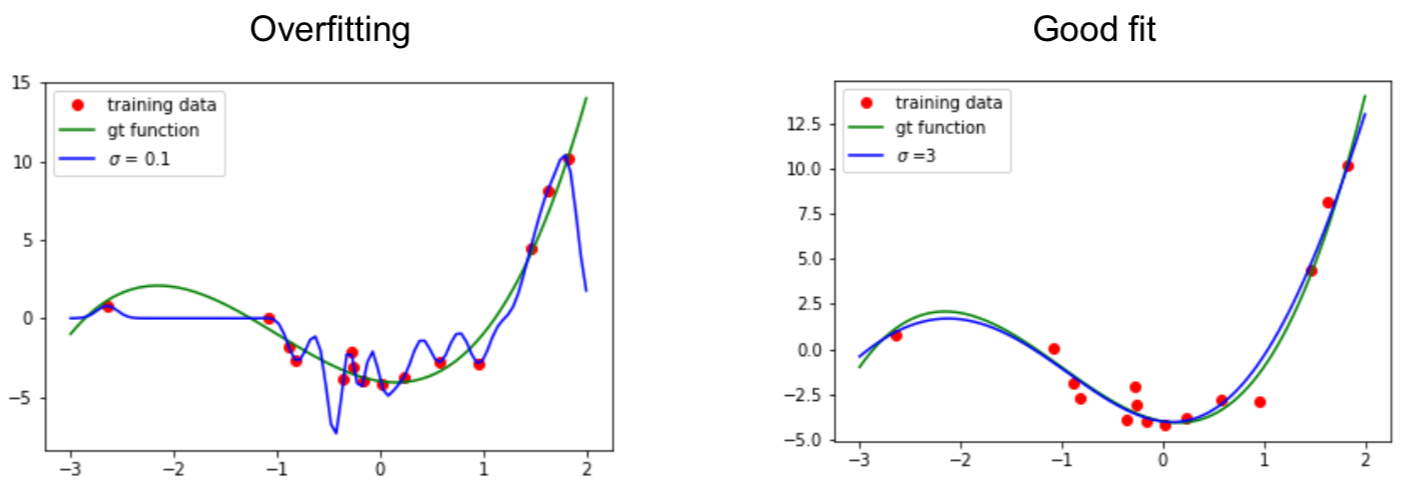
$$ f(\boldsymbol{x})=\sum_{i} \alpha_{i} k\left(\boldsymbol{x}_{i}, \boldsymbol{x}\right)=\sum_{i} \alpha_{i} \exp \left(-\frac{\left\|\boldsymbol{x}-\boldsymbol{x}_{i}\right\|^{2}}{2 \sigma^{2}}\right) $$Select hyperparameter
Bandwidth parameter $\sigma$ in Gaussian kernel
$$ k(\boldsymbol{x}, \boldsymbol{y})=\exp \left(-\frac{\|\boldsymbol{x}-\boldsymbol{y}\|^{2}}{2 \sigma^{2}}\right) $$are called hyperparameters.
How to choose? Cross validation!
Example:
Summary: kernel ridge regression
The solution for kernel ridge regression is given by
$$ f^{*}(\boldsymbol{x})=\boldsymbol{k}(\boldsymbol{x})^{T}(\boldsymbol{K}+\lambda \boldsymbol{I})^{-1} \boldsymbol{y} $$- No evaluation of the feature vectors needed 👏
- Only pair-wise scalar products (evaluated by the kernel) 👏
- Need to invert a $\color{red}{N \times N}$ matrix (can be costly) 🤪
‼️Note:
Have to store all samples in kernel-based methods
- Computationally expensive (matrix inverse is $O(n^{2.376})$) !
Hyperparameters of the method are given by the kernel-parameters
- Can be optimized on validation-set
Very flexible function representation, only few hyper-parameters 👍