Polynomial Regression (Generalized linear regression models) 💡Idea Use a linear model to fit nonlinear data :
add powers of each feature as new features, then train a linear model on this extended set of features.
Generalize Linear Regression to Polynomial Regression In Linear Regression f f f x \boldsymbol{x} x w \boldsymbol{w} w
f ( x ) = x ^ T w
f(x) = \hat{\boldsymbol{x}}^T \boldsymbol{w}
f ( x ) = x ^ T w
Rewrite it more generally:
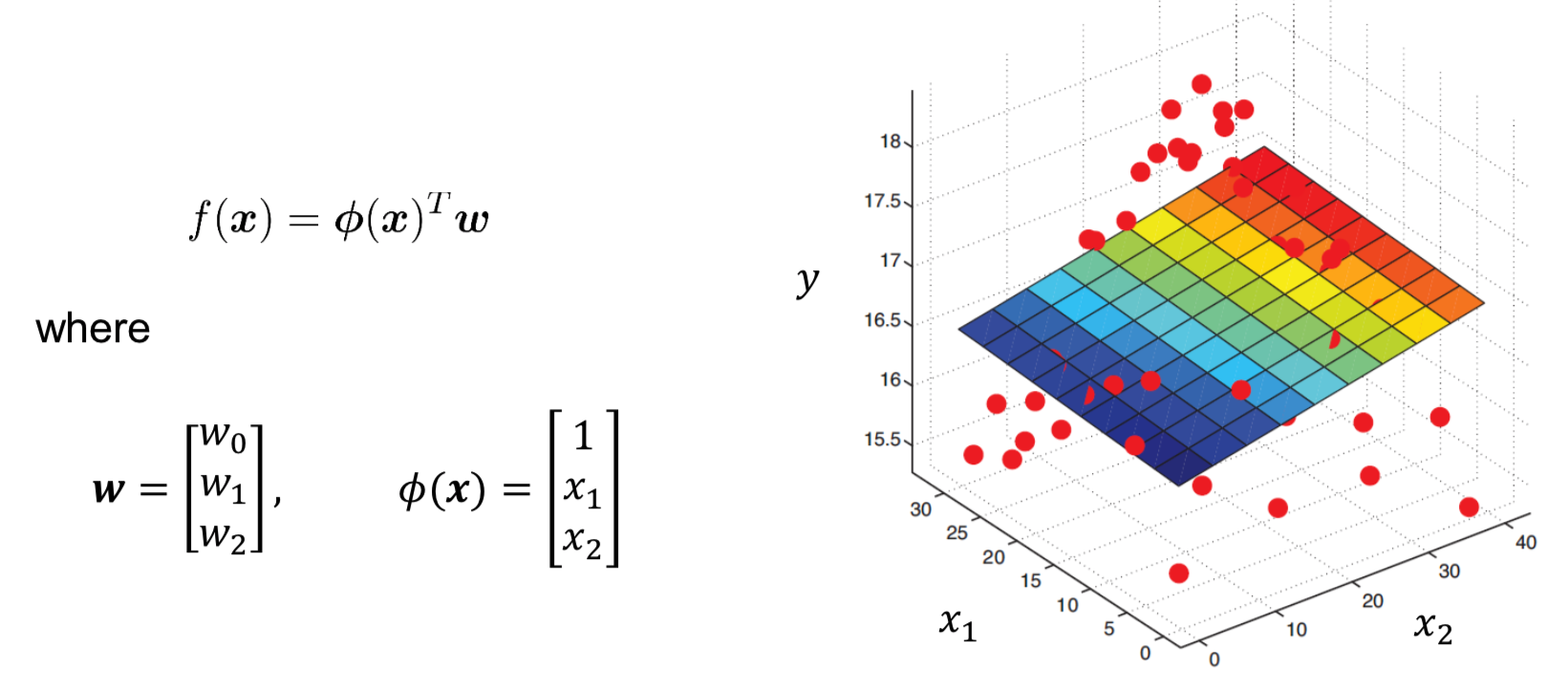
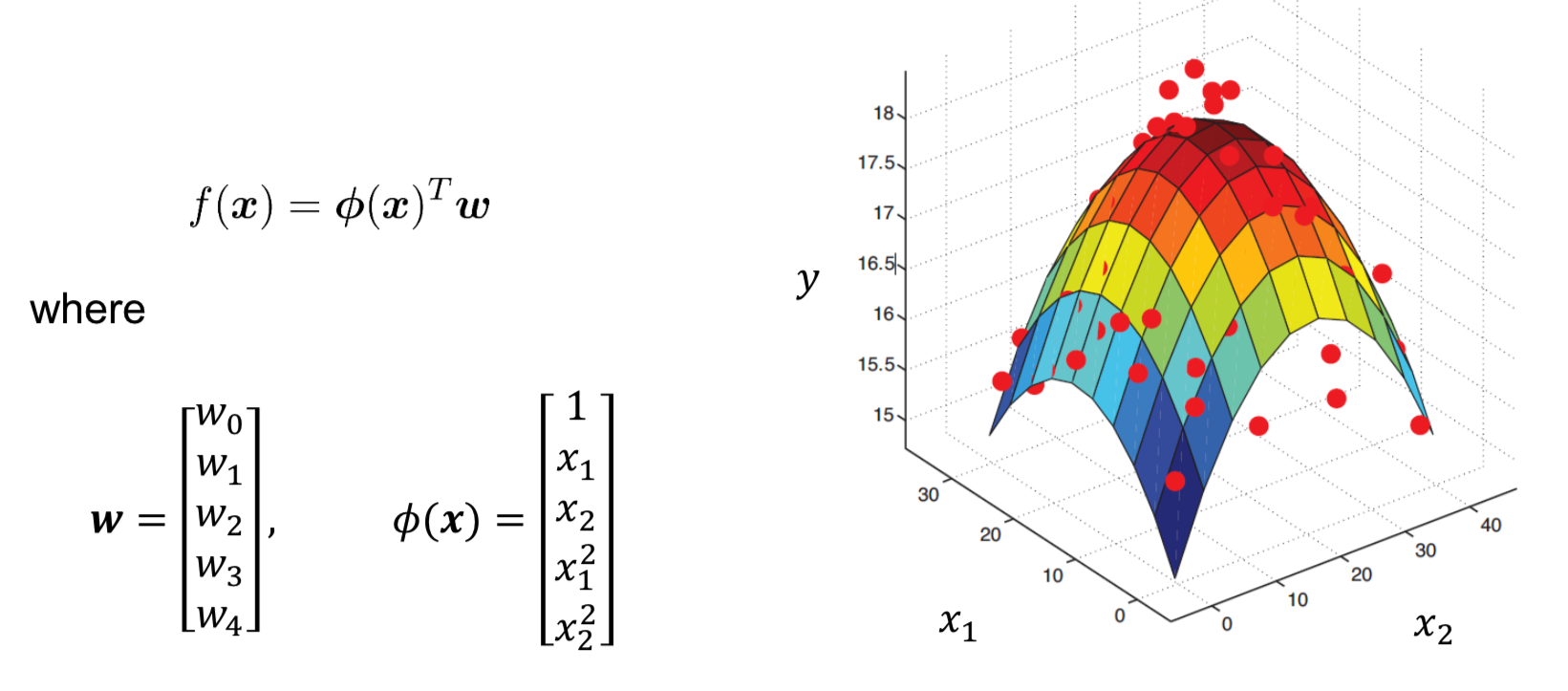
f ( x ) = ϕ ( x ) T w
f(x) = \phi(\boldsymbol{x})^T \boldsymbol{w}
f ( x ) = ϕ ( x ) T w
ϕ ( x ) \phi(\boldsymbol{x}) ϕ ( x ) x \boldsymbol{x} x linear basis function models ”)ϕ i ( x ) \phi_i(\boldsymbol{x}) ϕ i ( x ) basis functions In principle, this allows us to learn any non-linear function , if we know suitable basis functions (which is typically not the case 🤪).
Example 1 x = [ x 1 x 2 ] ∈ R 2 \boldsymbol{x}=\left[\begin{array}{c}{x_1 \\ x_2}\end{array}\right] \in \mathbb{R}^{2} x = [ x 1 x 2 ] ∈ R 2
ϕ : R 2 → R 3 , [ x 1 x 2 ] ↦ [ 1 x 1 x 2 ] \phi: \mathbb{R}^2 \to \mathbb{R}^3, \left[\begin{array}{c}{x_1 \\ x_2}\end{array}\right] \mapsto \left[\begin{array}{c}{1 \\ x_1 \\ x_2}\end{array}\right]\qquad ϕ : R 2 → R 3 , [ x 1 x 2 ] ↦ [ 1 x 1 x 2 ] ϕ 1 ( x ) = 1 , ϕ 2 ( x ) = x 1 , ϕ 3 ( x ) = x 2 \phi_1(\boldsymbol{x}) = 1, \phi_2(\boldsymbol{x}) = x_1, \phi_3(\boldsymbol{x}) = x_2 ϕ 1 ( x ) = 1 , ϕ 2 ( x ) = x 1 , ϕ 3 ( x ) = x 2
Example 2 x = [ x 1 x 2 ] ∈ R 2 \boldsymbol{x}=\left[\begin{array}{c}{x_1 \\ x_2}\end{array}\right] \in \mathbb{R}^{2} x = [ x 1 x 2 ] ∈ R 2
ϕ : R 2 → R 5 , [ x 1 x 2 ] ↦ [ 1 x 1 x 2 x 1 2 x 2 2 ] \phi: \mathbb{R}^2 \to \mathbb{R}^5, \left[\begin{array}{c}{x_1 \\ x_2}\end{array}\right] \mapsto \left[\begin{array}{c}{1 \\ x_1 \\ x_2 \\ x_1^2 \\ x_2^2}\end{array}\right] ϕ : R 2 → R 5 , [ x 1 x 2 ] ↦ [ 1 x 1 x 2 x 1 2 x 2 2 ]
Optimal value of w \boldsymbol{w} w w ∗ = ( Φ T Φ ) − 1 Φ T y , Φ = [ ϕ 1 T ⋮ ϕ n T ]
\boldsymbol{w}^{*}=\left(\boldsymbol{\Phi}^{T} \boldsymbol{\Phi}\right)^{-1} \boldsymbol{\Phi}^{T} \boldsymbol{y}, \qquad \mathbf{\Phi}=\left[\begin{array}{c}{\phi_{1}^{T}} \\\\ {\vdots} \\\\ {\phi_{n}^{T}}\end{array}\right]
w ∗ = ( Φ T Φ ) − 1 Φ T y , Φ = ϕ 1 T ⋮ ϕ n T
(The same as in Linear Regression, just the data matrix is now replaced by the basis function matrix)
Challenge of Polynomial Regression: Overfitting Reason:
Too complex model (Degree of the polynom is too high!). It fits the noise and has unspecified behaviour between the training points.😭
Solution: Regularization
Regularization Regularization: Constrain a model to make it simpler and reduce the task of overfitting.
💡 Avoid overfitting by forcing the weights w \boldsymbol{w} w
Assume that our model has degree of 3 (x 1 , x 2 , x 3 x^1, x^2, x^3 x 1 , x 2 , x 3 w 1 , w 2 , w 3 w_1, w_2, w_3 w 1 , w 2 , w 3 w 3 = 0 w_3=0 w 3 = 0 w 3 x 3 = 0 w_3 x^3 = 0 w 3 x 3 = 0
In general, a regularized model has the following cost/objective function:
E _ D ( w ) ⏟ _ Data term + λ E _ W ( w ) ⏟ _ Regularization term
\underbrace{E\_D(\boldsymbol{w})}\_{\text{Data term}} + \underbrace{\lambda E\_W(\boldsymbol{w})}\_{\text{Regularization term}}
E _ D ( w ) _ Data term + λ E _ W ( w ) _ Regularization term λ \lambda λ
Regularized Least Squares (Ridge Regression) Consists of:
Sum of Squareds Error (SSE) functionquadratic regulariser (L 2 L_2 L 2 L ridge = S S E + λ ∥ w ∥ 2 = ( y − Φ w ) T ( y − Φ w ) + λ w T w
\begin{aligned}
L_{\text {ridge }}
&= \mathbf{SSE} + \lambda \|w\|^2 \\\\
&= (\boldsymbol{y}-\boldsymbol{\Phi} \boldsymbol{w})^{T}(\boldsymbol{y}-\boldsymbol{\Phi} \boldsymbol{w})+\lambda \boldsymbol{w}^{T} \boldsymbol{w}
\end{aligned}
L ridge = SSE + λ ∥ w ∥ 2 = ( y − Φ w ) T ( y − Φ w ) + λ w T w
Solution:
w r i d g e ∗ = ( Φ T Φ + λ I ) − 1 Φ T y \boldsymbol{w}_{\mathrm{ridge}}^{*}=\left(\boldsymbol{\Phi}^{T} \boldsymbol{\Phi}+\lambda \boldsymbol{I}\right)^{-1} \boldsymbol{\Phi}^{T} \boldsymbol{y} w ridge ∗ = ( Φ T Φ + λ I ) − 1 Φ T y
I \boldsymbol{I} I ( Φ T Φ + λ I ) \left(\boldsymbol{\Phi}^{T} \boldsymbol{\Phi}+\lambda \boldsymbol{I}\right) ( Φ T Φ + λ I )