Word Sense Disambiguation
Introduction
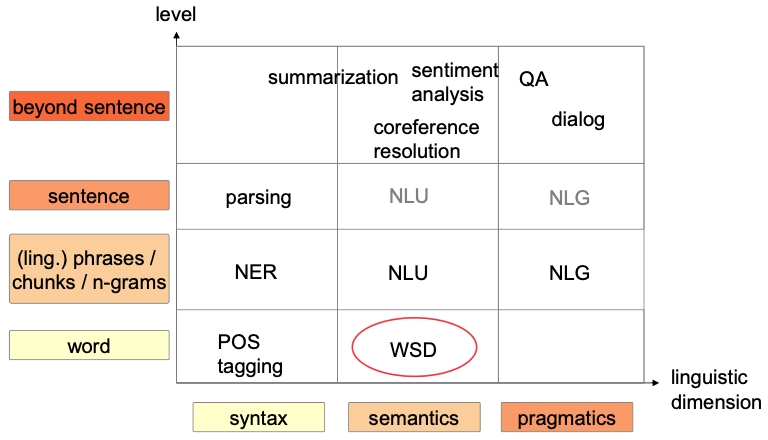
Definition
Word Sense Disambiguation
- Determine which sense/meaning of a word is used in a particular context
- Classification problem
Sense inventory
- considered senses of the words
Word Sense Discrimination
- Divide usages of a word into different meanings
- Unsupervised Algorithms
Task
Determine which sense of a word is activated in a context
Find mapping for word :
- Mostly
Model as classification problem:
- Assign sense based on context and external knowledge sources
- Every word has different number of classes
- distinct classification tasks ( Vocabulary size)
Task-conditions
Word senses
- Finite set of senses for every word
- Automatic clustering of word senses
Sense inventories
- coarse-grained
- fine-grained
Text characteristics
- domain-oriented
- unrestricted
Target words
- one target word per sentence
- all words
Resources
- Annotated data
- Input data X and output/label data Y
- Hard to acquire, but important
- Supervised training
- Unlabeled data
- Input data X
- Large amounts
- Unsupervised data
- Structured resources
- Thesauri
- Machine-readable dictionaries (MRDs)
- Computation lexicon (Wordnet)
- Ontologies
- Unstructured resources
- Corpora
- Collocations resources
🔴 Problems
- Sense definition is task dependent
- Different algorithms for different applications
- No discrete sense division possible
- Knowledge acquisition bottleneck
- Intermediate task
Application
- Machine Translation (MT)
- Information Retrieval (IR)
- Question Answering (QA)
- Semantic interpretation
Approaches
Dictionary- and Knowledge-Based
Lesk method / Gloss overlap
💡 Idea: Word used together in a text are related
Method: Find word sense with the most overlap of dictionary definition
Input: Dictionary with definition of the different word sense
Overlap calculation
Two words and
For each pair of senses in and in :
Problem: Many words in the context -> calculation very slow 🤪
Variant (simplified): Calculate overlap between context (set of words in surrounding sentence or paragraph) and gloss:
Example:

Problems:
- depend heavily on the exact definition
- definitions are often very short
Supervised
💡 Train classifier using annotated examples (i.e., annotated text corpora)
- Input features: Use context to disambiguate words
- Problems:
- high-dimension of the feature space
- data sparseness problem
- Techniques:
- Naive Bayes classifier
- Instance-based Learning
- SVM
- Ensemble Methods
- Neural Networks (e.g. Bi-LSTM)
Feature extraction
Feature vector:
- Vector describing input data
- Fixed number of dimensions
- Challenges:
- Variable sentence length
- Unknown number of words
- Challenges:
Two kinds of features in the vectors:
Collocational: Features about words at specific positions near target word
Think as a (ordered) list
Often limited to just word identity and POS
Example:

Bag-of-words: Features about words that occur anywhere in the window (regardless of position)
Think as “an unordered set of words”
Typically limited to frequency counts
How it works?
- Counts of words occur within the window.
- First choose a vocabulary
- Then count how often each of those terms occurs in a given window
- sometimes just a binary “indicator” 1 or 0
Example:

Text processing
- Tokenization
- Part-of-speech tagging
- Lemmatization
- Chunking: divided text into syntactically correlated part
- Parsing
Feature definition
- Local features
- surrounding words, POS tags, position with respect to target word
- Topical/Global features
- general topic of a text
- mostly bag-of-words representation of (sentence, paragraph, …)
- Syntactic features
- syntactic clues
- can be outside the local context
- Semantic features
- previous determined sense of words in the context
Naive Bayes classifier
Input:
a word in a text window (which we’ll call a “document”)
a fixed set of classes
A training set of hand-labeled text windows again called
“documents”
Output: a learn classifier
: prior probability of that sense
- Counting in a labeled training set
: conditional probability of a word given a particular sense
(We get both of these from a tagged corpus)
Example:
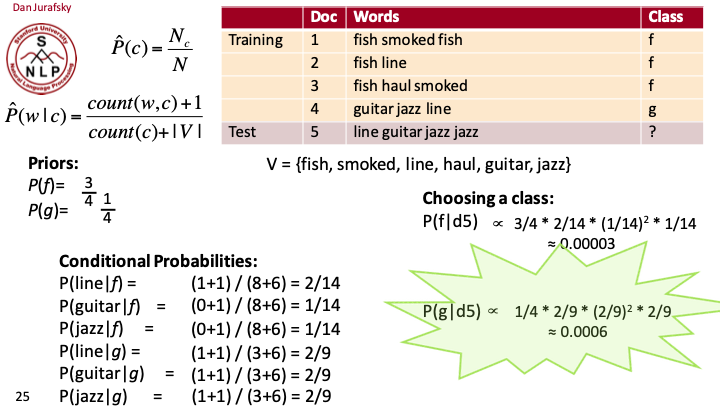
Example of naive bayes classfier
Instance-based Learning
Build classification model based on examples
k-Nearest Neighbor (k-NN) algorithm
💡Idea:
- represent examples in vector space
- define distance metric in vector space
- find nearest neighbor
- take most common sense in the k nearest neighbors
Distance: e.g., Hamming distance
- if else 1
- : weight (e.g., Gain ration measure)
In information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different. In other words, it measures the minimum number of substitutions required to change one string into the other, or the minimum number of errors that could have transformed one string into the other.
Example:

Ensemble Methods
Combine different classifier
- classifier have strength in different situation
- improve by asking several experts
Algorithm:
Score input by several First-order classifier
Combine results
Result:
Only best hypothesis (majority vote)
take decision of most classifiers
if tie, randomly choose between them
Score for all hypothesis (Probability Mixture)
Normalize scores of every classifier to get probability
Take class with highest sum of probabilities
- Ranking of all hypothesis (Rank-based Combination)
Semi-supervised
‼️ Knowledge acquisition bottleneck: hard to get large amounts of annotated data
💡 Idea of Semi-supervised approaches:
- Some initial model trained on small amounts of annotated data
- Improve model using raw data
Bootstrapping
Seed data:
manual annotated
surefire decision rules
Train classifier on annotated data A
Select subset U’ of unlabeled data
Annotate U’ with classifier
Filter most reliable examples
Add examples to A
Repeat from training
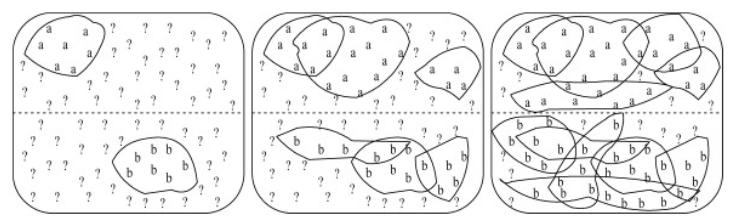
Self-training
- always use same classifier
Co-training
- train classifier 1 (e.g. using local feature)
- Annotate with classifier 1
- train classifier 2 (e.g. topical information) on and A
- Annotate with classifier 2
- train classifier 1 …
Unsupervised
💡 Idea
- If a word is used in similar context, the meaning should be similar
- If the word is used in completely different context, different meaning
Approach: Cluster contexts of words
Context clustering
Word space model:
Vector space with dimension of the words
vector for word :
- -th component: number of co-occurs of and
Similarity:
Example:
- Dimension: (food, bank)
- restaurant=(210, 80)
- money = (100, 250)
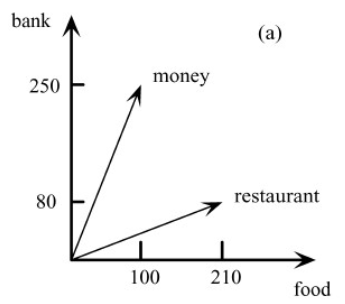
‼️ Problem:
- sparse representation
- latent semantic analyses (LSA)
Context representation
Second-order vectors: average of all word vectors in the context
Example:
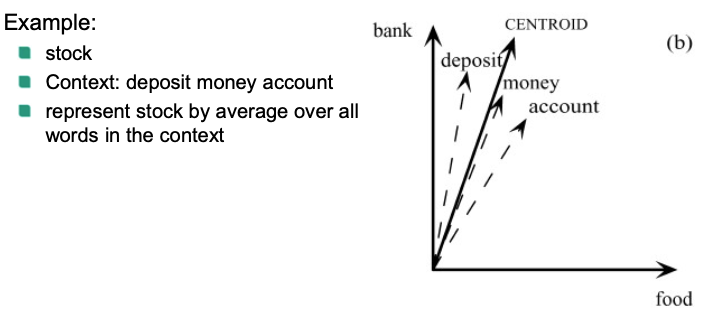
Cluster contexts
- Agglomerative clustering
- Start with one context per cluster
- Merge most similar clusters
- Continue until threshold is reached
Co-occurrence Graphs
HyperLex: Co-occurrence graph for one target ambiguous word
Nodes: All Words occurring in a paragraph with
Edge: words occur in same paragraph
Weight:
Low weight -> High probability of co-occurring
Discard edges with very high weight
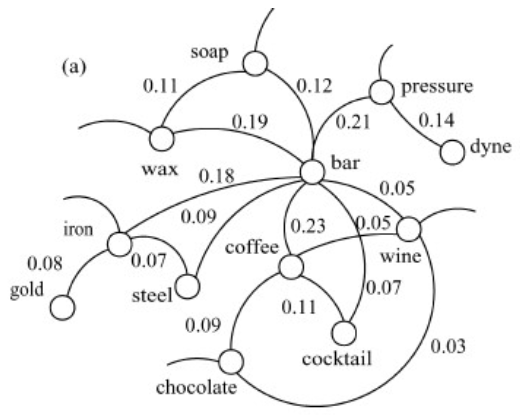
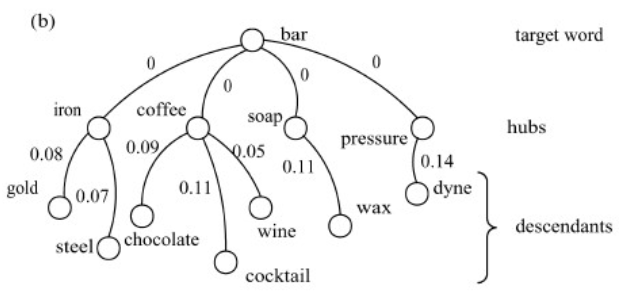
How HyperLex works?
Select Hubs (Nodes with highest degree)
Connect target words with weight 0 to hubs
Calculate Minimal Spanning Tree
See Target word in Context
Calculate vector for every word with (if ancestor of )
Sum all vectors and assign to hub with highest sum
Evaluation
Hand-annotated data
Precision
Recall
Task:
Lexical sample: only some words need to be disambiguate
All-words: all words need to be disambiguate
Baseline:
Random baseline: Randomly choose one class
First Sense Baseline: Always take most common sense