Part-of-Speech Tagging
Part-of-Speech Tagging
What is Part-of-Speech Tagging?
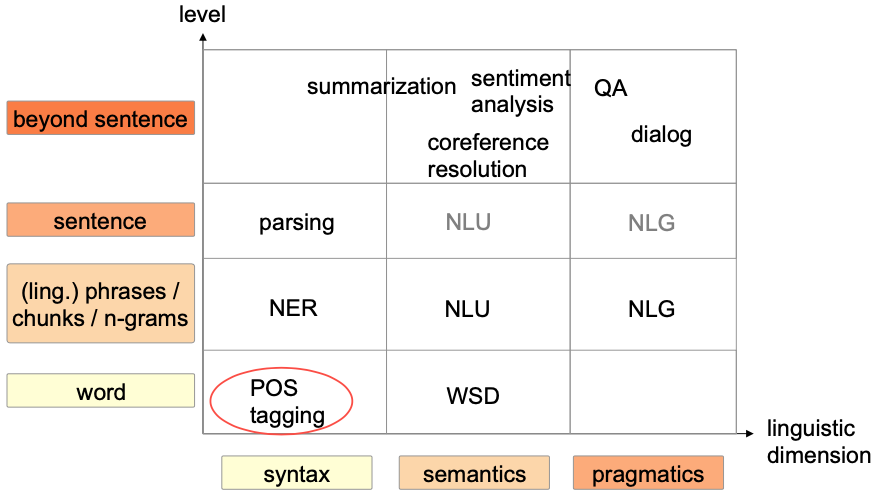
Part-of-Speech tagging:
Grammatical tagging
Word-category disambiguation
Task: Marking up a word in a text as corresponding to a particular part of speech
- based on definition and context
Word level task: Assign one class to every word
Variations:
English schools: 9 POS
- noun, verb, article, adjective, preposition, pronoun, adverb, conjunction, and interjection.
POS-tagger: 50 – 150 classes
- Plural, singular
POS + Morph tags:
- More than 600
- Gender, case, …
Data sources
Brown corpus
Penn Tree Bank
Tiger Treebank
🔴 Problems
- Ambiguities
- E.g.: “A can of beans” vs. “We can do it”
- Many content words in English can have more than 1 POS tag
- E.g.: play, flour
- Data sparseness: What to do with rare words?
Disambiguate using context information 💪
Example applications
- Information extraction
- QA
- Shallow parsing
- Machine Translation
How to do POS Tagging?
Rule-based
Rule-based taggers use dictionary or lexicon for getting possible tags for tagging each word. If the word has more than one possible tag, then rule-based taggers use hand-written rules to identify the correct tag. Disambiguation can also be performed in rule-based tagging by analyzing the linguistic features of a word along with its preceding as well as following words. For example, suppose if the preceding word of a word is article then word must be a noun.
Design rules to assign POS tags to words
How can one decide on the right POS tag used in a context?
Two sources of information:
- Tags of other words in the context of the word we are interested in
- knowing the word itself gives a lot of information about the correct tag
Syntagmatic approach
most obvious source of information
With rule-based approach only 77% tagged correctly 🤪
Example
Should play get an
NNorVBPtag?Take the more common POS tag sequence for phrase a new play:
ATJJNNvs.ATJJVBP
Lexical information
assign the most common tag to a word
90% correct !!! (favorable conditions)
So useful because the distribution of a word’s usages across different POS is typically extremely uneven → usually occur as 1 POS
All modern taggers use a combination of syntagmatic and lexical information.
Statistical approaches should work well on POS tagging, assuming a word has different POS tags according certain a priori probabilities
Brill-Tagger
Developed by Eric Brill in 1995
Algorithm
Initialize:
- Every word gets most frequent POS
- Unknown: Noun
Until no longer possible
- Apply rules
Rules
- Linguistically motivated
- Machine learning algorithms
Wiki:
The Brill tagger is an inductive method for part-of-speech tagging. It can be summarized as an “error-driven transformation-based tagger”.
It is:
- a form of supervised learning, which aims to minimize error; and,
- a transformation-based process, in the sense that a tag is assigned to each word and changed using a set of predefined rules.
In the transformation process,
- if the word is known, it first assigns the most frequent tag,
- if the word is unknown, it naively assigns the tag “noun” to it.
Applying over and over these rules, changing the incorrect tags, a quite high accuracy is achieved.
Statistical
Probabilistic tagging: Model POS tags as Sequence labeling
Wiki:
In machine learning, sequence labeling is a type of pattern recognition task that involves the algorithmic assignment of a categorical label to each member of a sequence of observed values.
A common example of a sequence labeling task is part of speech tagging, which seeks to assign a part of speech to each word in an input sentence or document. Sequence labeling can be treated as a set of independent classification tasks, one per member of the sequence. However, accuracy is generally improved by making the optimal label for a given element dependent on the choices of nearby elements, using special algorithms to choose the globally best set of labels for the entire sequence at once.
Sequence labeling
Input: sequence
Output: Sequence
Example

Model as Machine Learning Problem
💡 Classify each token independently but use as input features, information about the surrounding tokens (sliding window).
Training data
Label sequence \left\\{\left(x^{1}, y^{1}\right),\left(x^{2}, y^{2}\right), \ldots,\left(x^{M}, y^{M}\right)\right\\}
Learn model:
Problem: Exponential number of solutions!!!
Number of solutions: \text{#Classes}^{\text{#Words}}
-> Can NOT directly model or 🤪
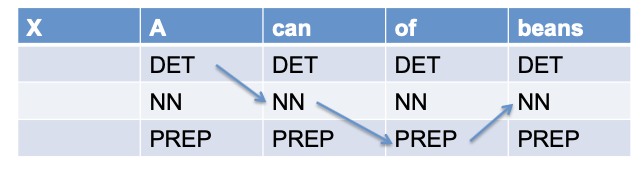
The model that includes frequency or probability (statistics) can be called stochastic. Any number of different approaches to the problem of part-of-speech tagging can be referred to as stochastic tagger.
Decision Trees
Automatically learn which question to ask
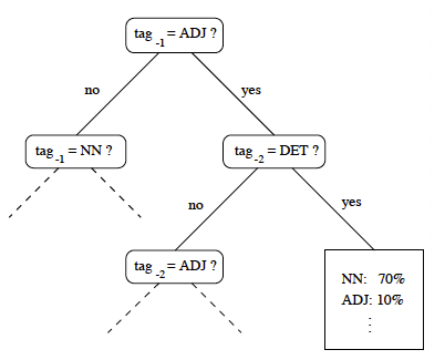
Probabilistic tagging
- Define probability for tag sequence recursively
- Using two models
- : model using decision tree
- Lexicon
- Suffix lexicon for unknown words
- Which POS tag attached to unknown words
- Depending on the ending some POS tags are more probable
Condition Random Fields (CRFs)
Wiki:
Conditional random fields (CRFs) are a class of statistical modeling method often applied in pattern recognition and machine learning and used for structured prediction. Whereas a classifier predicts a label for a single sample without considering “neighboring” samples, a CRF can take context into account.
Hidden Markov Model (HMM):
- Hidden states: POS
- Output: Words
- Task: Estimate state sequence from output
Generative model
Assign a joint probability to paired observation and label sequences
Problem when modeling
Introduce highly dependent features
Example: Word, Capitalization, Suffix, Prefix
Possible solutions:
Model dependencies
- How does the capitalization depend on the suffix?
Independence assumption
- Hurts performance
Discriminative Model
- Directly model
- No model for is involved
- Not needed for classification since x is observed
Linear Chain Conditional Random Fields
- : random variable (Representing the input)
- : random variable (POS tags)
- : Parameter
- : feature function
Model:
p(\mathbf{y} | \mathbf{x})=\frac{1}{Z(\mathbf{x})} \prod\_{t=1}^{T} \exp \left\\{\sum\_{k=1}^{K} \theta\_{k} f\_{k}\left(y\_{t}, y\_{t-1}, \mathbf{x}\_{t}\right)\right\\} Z(\mathrm{x})=\sum\_{\mathbf{y}} \prod\_{t=1}^{T} \exp \left\\{\sum\_{k=1}^{K} \theta\_{k} f\_{k}\left(y\_{t}, y\_{t-1}, \mathbf{x}\_{t}\right)\right\\}Feature functions
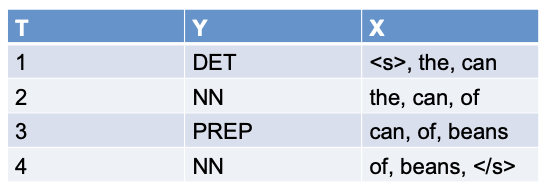
First-order dependencies
Lexical:
Lexical with context:
Additional features:
Inference
Task: Get most probabale POS sequence
Problem: Exponential number of label sequences 🤪
Linear-chain layout
Dynamic programming can be used
Efficient computing
Training
Task: How to find the best weight ?
💡 Maximum (Log-)Likelihood estimation
Maximize probability of the training data
Given: sequence with labels
Maximize
Regularization
Prevent overfitting by prefering lower weights
Convex function
Can use gradient descent to find optimal value 👏
Neural Network
🔴 Data sparseness Problem
- Many words have rarely seen in training Hard to estimate probabilities 🤪
- CRFs:
- Use many features to represent the word
- Problem: A lot of engineering!
Neural networks
Able to learn hidden representation
Learn representation of words based on letters, E.g.:
- Words ending on ness with be
nouns - Words ending on phoby will be
nouns - Words ending on ly are often
adverbs
- Words ending on ness with be
Structure
- First layer: Word representation
CNN
Learn mapping: Word continuous vector
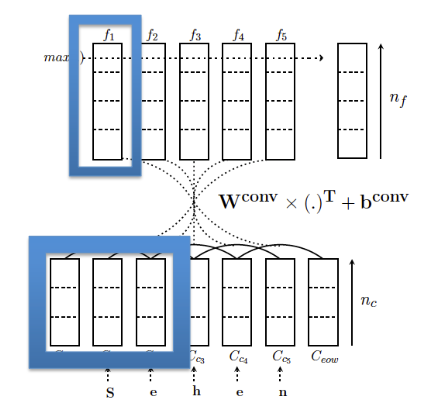
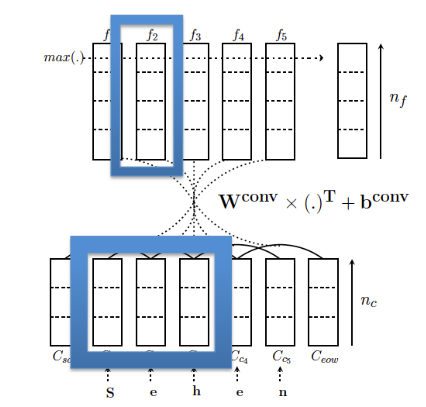
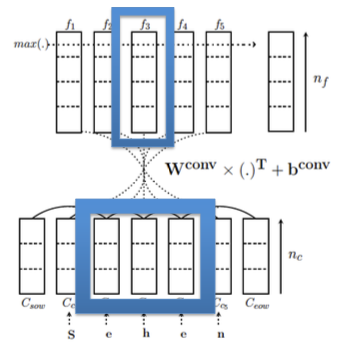
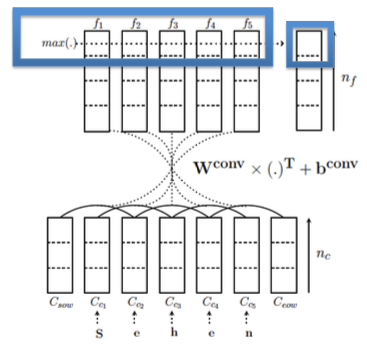
Second layer:
- Use several words to predict POS tag
- Feed forward net
- RNN: Contain complete history
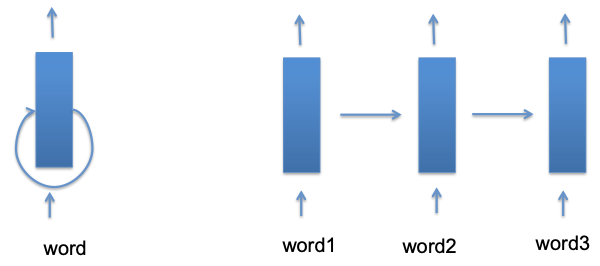
Training
Train both layers together using backpropagation