Named Entity Recognition
Introduction
Definition
Named Entity: some entity represented by a name
Named Entity Recognition: Find and classify named entities in text
Why useful?
Create indices & hyperlinks
Information extraction
- Establish relationships between named entities, build knowledge base
Question answering: answers often NEs
Machine translation: NEs require special care
- NEs often unknown words, usually passed through without translation.
Why difficult?
World knowledge
Non-local decisions
Domain specificity
Labeled data is very expensive
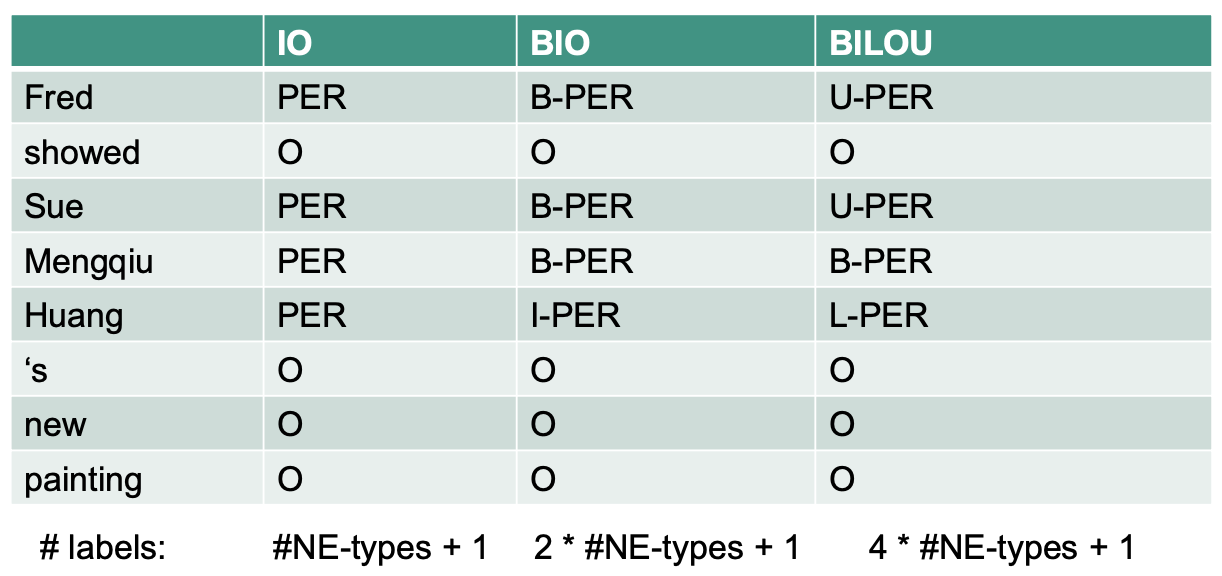
Label Representation
IO
- I: Inside
- O: Outside (indicates that a token belongs to no chunk)
BIO
B: Begin
The IOB format (short for inside, outside, beginning), a synonym for BIO format, is a common tagging format for tagging tokens in a chunking task in computational linguistics.
- B-prefix before a tag: indicates that the tag is the beginning of a chunk
- I-prefix before a tag: indicates that the tag is the inside of a chunk
- O tag: indicates that a token belongs to NO chunk
BIOES
- E: Ending character
- S: single element
BILOU
- L: Last character
- U: Unit length
Example:
Fred showed Sue Mengqiu Huang's new painting
Data
- CoNLL03 shared task data
- MUC7 dataset
- Guideline examples for special cases:
- Tokenization
- Elision
Evaluation
Precision and Recall
$$ \text{Precision} = \frac{\\# \text { correct labels }}{\\# \text { hypothesized labels }} = \frac{TP}{TP + FP} $$ $$ \text{Recall} = \frac{\\# \text { correct labels }}{\\# \text { reference labels }} = \frac{TP}{TP + FN} $$Phrase-level counting
System 1:
- “$\text{\\$200,000,000}$" is correctly recognized as NE $\Rightarrow$ TP =1
- “First Bank of Chicago” is incorrectly recognised as non-NE (i.e., O) $\Rightarrow$ FN = 1
Therefore:
$\text{Precision} = \frac{1}{1 + 0} = 1$
- $\text{Recall} = \frac{1}{1 + 1} = \frac{1}{2}$
System 2:
“$\text{\\$200,000,000}$" is correctly recognized as NE $\Rightarrow$ TP =1
For “First Bank of Chicago”
Word Actual label Predicted label First ORG O Bank of Chicago ORG ORG There’s a boundary error (since we consider the whole phrase):
- FN = 1
- FP = 1
Therefore:
$\text{Precision} = \frac{1}{1 + 1} = \frac{1}{2}$
$\text{Recall} = \frac{1}{1 + 1} = \frac{1}{2}$
- Problems
- Punish partial overlaps
- Ignore true negatives
Token-level
In token-level, we consider these tokens: “First”, “Bank”, “of”, “Chicago”, and “$200,000,000”
System 1
- “$\text{\\$200,000,000}$" is correctly recognized as NE $\Rightarrow$ TP =1
- “First”, “Bank”, “of”, “Chicago” are incorrectly recognised as non-NE (i.e., O) $\Rightarrow$ FN = 4
Therefore:
$\text{Precision} = \frac{1}{1 + 0} = 1$
$\text{Recall} = \frac{1}{1 + 4} = \frac{1}{5}$
- Partial overlaps rewarded!
- But
longer entities weighted more strongly
True negatives still ignored 🤪
$F\_1$ score (harmonic mean of precision and recall)
$$ F\_1 = \frac{2 \times \text { precision } \times \text { recall }}{\text { precision }+\text { recall }} $$
Text Representation
Local features
Previous two predictions (tri-gram feature)
- $y\_{i-1}$ and $y\_{i-2}$
Current word $x\_i$
Word type $x\_i$
- all-capitalized, is-capitalized, all-digits, alphanumeric, …
Word shape
lower case - ‘x’
upper case - ‘X’
numbers - ’d'
retain punctuation
Word substrings
Tokens in window
Word shapes in window
…
Non-local features
Identify tokens that should have same labels
Type:
Context aggregation
Derived from all words in the document
No dependencies on predictions, usable with any inference algorithm
Prediction aggregation
Derived from predictions of the whole document
Global dependencies; Inference:
first apply baseline without non-local features
then apply second system conditioned on output of first system
Extended prediction history
Condition only on past predictions –> greedy / beam search
💡 Intuition: Beginning of document often easier, later in document terms often get abbreviated
Sequence Model
HMMs
Generative model
Generative story:
Choose document length $N$
For each word $t = 0, \dots, N$:
Draw NE label $\sim P(y\_t | y\_{t-1})$
Draw word $\sim P\left(x\_{t} | y\_{t}\right)$
$$ P(\mathbf{y}, \mathbf{x})=\prod P\left(y\_{t} | y\_{t-1}\right) P\left(x | y\_{t}\right) $$
Example
👍 Pros
- intuitive model
- Works with unknown label sequences
- Fast inference
👎 Cons
- Strong limitation on textual features (conditional independence)
- Model overly simplistic (can improve the generative story but would lose fast inference)
Max. Entropy
Discriminative model $P(y\_t|x)$
Don’t care about generation process or input distribution
Only model conditional output probabilities
👍 Pros: Flexible feature design
👎 Cons: local classifier -> disregard sequence information
CRF
Discriminative model
👍 Pros:
Flexible feature design
Condition on local sequence context
Training as easy as MaxEnt
👎 Cons: Still no long-range dependencies possible
Modelling
Difference to POS
- Long-range dependencies
- Alternative resources can be very helpful
- Several NER more than one word long
Example
Inference
Viterbi
- Finds exact solution
- Efficient algorithmic solution using dynamic programming
- Complexity exponential in order of Markov model
- Only feasible for small order
Greedy
At each timestep, choose locally best label
Fast, support conditioning on global history (not future)
No possibility for “label revision”
Beam
- Keep a beam of the $n$ best greedy solutions, expand and prune
- Limited room for label revisions
Gibbs Sampling
Stochastic method
Easy way to sample from multivariate distribution
Normally used to approximate joint distributions or intervals
$$ P\left(y^{(t)} | y^{(t-1)}\right)=P\left(y\_{i}^{(t)} | y\_{-i}^{(t-1)}, x\right) $$- $-1$ means all states except $i$
💡 Intuitively:
- Sample one variable at a time, conditioned on current assignment of all other variables
- Keep checkpoints (e.g. after each sweep through all variables) to approximate distribution
In our case:
Initialize NER tags (e.g. random or via Viterbi baseline model)
Re-sample one tag at a time, conditioned on input and all other tags
After sampling for a long time, we can estimate the joint distribution over outputs $P(y|x)$
However, it’s slow, and we may only be interested in the best output 🤪
Could choose best instead of sampling
$$ y^{(t)}=y\_{-i}^{(t-1)} \cup \underset{y\_{i}^{(t)}}{\operatorname{argmax}}\left(P\left(y\_{i}^{(t)} | y\_{-i}^{(t-1)}, x\right)\right) $$- will get stuck in local optima 😭
Better: Simulated annealing
- Gradually move from sampling to argmax $$ P\left(y^{(t)} | y^{(t-1)}\right)=\frac{P\left(y\_{i}^{(t)} | y\_{-i}^{(t-1)}, x\right)^{1 / c\_{t}}}{\displaystyle\sum\_{j} P\left(y\_{j}^{(t)} | y\_{-j}^{(t-1)}, x\right)^{1 / c\_{t}}} $$
External Knowledge
Data
Supervised learning:
- Label Data:
- Text
- NE Annotation
- Label Data:
Unsupervised learning
- Unlabeled Data: Text
- Problem: Hard to directly learn NER
Semi-supervised: Labeled and Unlabeled Data
Word Clustering
Problem: Data Sparsity
Idea
Find lower-dimensional representation of words
real vector /probabilities have natural measure of similarity
Which words are similarr?
- Distributional notion
- if they appear in similar context, e.g.
- “president” and “chairman” are similar
- “cut” and “knife” not
Words in same cluster should be similar
Brown clusters
Bottom-up agglomerative word clustering
Input: Sequence of words $w\_1, \dots, w\_n$
Output
- binary tree
- Cluster: subtree (according to desired #clusters)
💡 Intuition: put syntacticly “exchangable” words in same cluster. E.g.:
Similar words: president/chairman, Saturday/Monday
Not similar: cut/knife
Algorithm:
Initialization: Every word is its own cluster
While there are more than one cluster
- Merge two clusters that maximizes the quality of the clustering
Result:
- Hard clustering: each word belongs to exactly one cluster
Quality of the clustering
Use class-based bigram language model
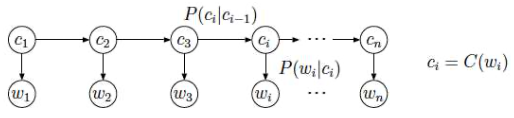
Quality: logarithm of the probability of the training text normalized by the length of the text
$$ \begin{aligned} \text { Quality }(C) &=\frac{1}{n} \log P\left(w\_{1}, \ldots, w\_{n}\right) \\\\ &=\frac{1}{n} \log P\left(w\_{1}, \ldots, w\_{n}, C\left(w\_{1}\right), \ldots, C\left(w\_{n}\right)\right) \\\\ &=\frac{1}{n} \log \prod\_{i=1}^{n} P\left(C\left(w\_{i}\right) | C\left(w\_{i-1}\right)\right) P\left(w\_{i} | C\left(w\_{i}\right)\right) \end{aligned} $$Parameters: estimated using maximum-likelihood