Information Retrieval
Overview
Information Retrieval (IR):
finding material (usually documents) of an unstructured nature (usually text) that satisfies an information need from within large collections (usually stored on computers).
Use case / applications
- web search (most common)
- E-mail search
- Searching your laptop
- Corporate knowledge bases
- Legal information retrieval
Basic idea
Collection: A set of documents
- Assume it is a static collection for the moment
🎯 Goal: Retrieve documents with information that is relevant to the user’s information need and helps the user complete a task
Main idea
Compare document and query to estimate relevance
Components
- Representation: How to represent the document and query
- Metric: How to compare document and query
Evaluation of retrieved docs
“How good are the retrieved docs?”
- Precision: Fraction of retrieved docs that are relevant to the user’s information need
- Recall: Fraction of relevant docs in collection that are retrieved
Logic-based IR
- Find all text containing words
- Allow boolean operations between words
- Representation: Words occurring in the document
- Metric: Matching (with Boolean operations)
- Limitations
- Only exact matches
- No relevance metric 🤪
- Primary commercial retrieval tool for 3 decades.
- Many search systems you still use are Boolean:
- library catalog
- Mac OSX Spotlight
- Many search systems you still use are Boolean:
Example
“Which plays of Shakespeare contain the words Brutus AND Caesar but NOT Calpurnia?”
One could grep all of Shakespeare’s plays for Brutus and Caesar, then strip out lines containing Calpurnia
But this is not the answer 😢
- Slow (for large corpora)
- NOT Calpurnia is non-trivial
- Other operations (e.g.,find the word Romans near countrymen) not feasible
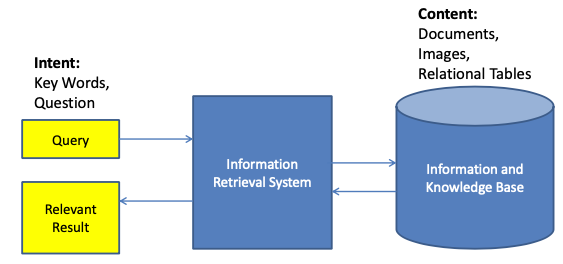
Incidence vectors

0/1 vector for each term
To answer the query in the example above:
take the vectors for Brutus, Caesar and Calpurnia (complemented), then bitwise AND.
- Brutus:
110100AND - Caesar:
110111AND - complemented Calpurnia:
101111 - =
100100
- Brutus:
However, this is not feasible for large collection! 😭
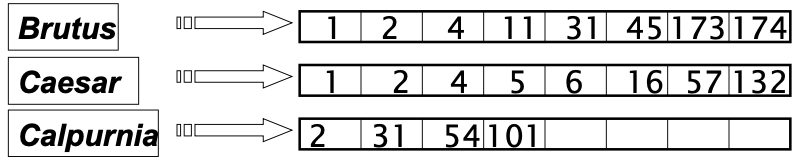
Inverted index
For each term , store a list of all documents that contain .
Identify each doc by a docID, a document serial number
Construction
- Collect the documents to be indexed
- Tokenize the text, turning each document into a list of tokens
- Do linguistic preprocessing, producing a list of normalized tokens, which are the indexing terms
- Index the documents that each term occurs in by creating an inverted index, consisting of a dictionary and postings
Example
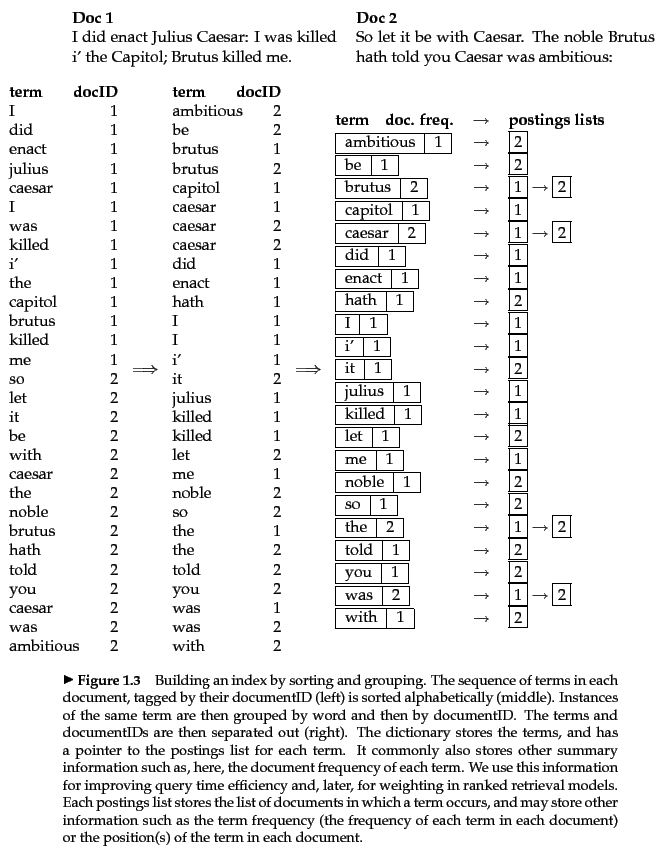
Initial stages of text processing
- Tokenization: Cut character sequence into word tokens
- Normalization: Map text and query term to same form
- E.g. We want
U.S.AandUSAto match
- E.g. We want
- Stemming: different forms of a root to match
- E.g.
authorizeandauthorizationshould match
- E.g.
- Stop words: we may omit very common words (or not)
- E.g.
the,a,to,of…
- E.g.
Query processing: AND
For example, consider processing the query: Brutus AND Caesar
Locate Brutus in the Dictionary
- Retrieve its postings
Locate Caesar in the Dictionary
- Retrieve its postings
“Merge” the two postings (intersect the document sets)

Walk through the two postings simultaneously, in time linear in the total number of postings entries
(If the list lengths are and , the merge takes operations.)
- ‼️Crucial: postings sorted by docID
Phrase queries
E.g. We want to be able to answer queries such as “stanford university” as a phrase
–> The sentence “I went to university at stanford” is not a match.
Implementation:
- Multi-words
- Position index
Rank-based IR
Motivation
Boolean queries: Documents either match or don’t.
Good for:
- expert users with precise understanding of their needs and the collection.
- applications: Applications can easily consume 1000s of results.
NOT good for the majority of users
- Most users incapable of writing Boolean queries (or they are, but they think it’s too much work).
- Most users don’t want to wade through 1000s of results.
🔴 Problem: feast of famine
- Often result in either too few (=0) or too many (1000s) results.
- It takes a lot of skill to come up with a query that produces a manageable number of hits.
- AND gives too few;
- OR gives too many
Ranked retrieval models
- Returns an ordering over the (top) documents in the collection for a query
- Free text queries: Rather than a query language of operators and expressions, the user’s query is just one or more words in a human language
- Large result sets are not an issue
Indeed, the size of the result set is not an issue
We just show the top (≈10) results
We don’t overwhelm the user
Premise: the ranking algorithm works
Representation:
Term weights (TF-IDF)
Word embeddings
Char Embeddings
Metric
Cosine similarity
Supervised trained classifier using clickthrough logs
Document similarity
Query-document matching scores
Assigning a score to a query/document pair
One-term query
- If the query term does not occur in the document: score should be 0
- The more frequent the query term in the document, the higher the score (should be)
Binary term-document incidence matrix
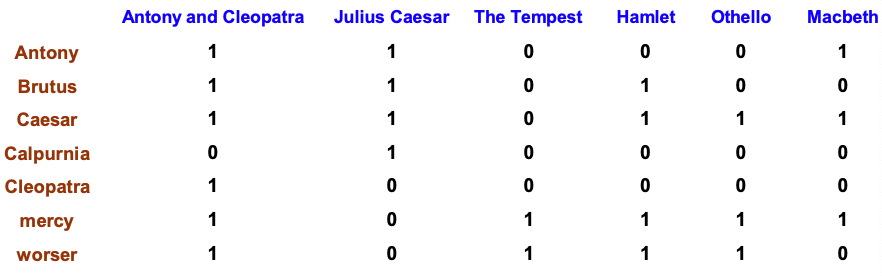
- Each document is represented by a binary vector
Term-document count matrices
Consider the number of occurrences of a term in a document
- Each document is a count vector in Nv: a column below
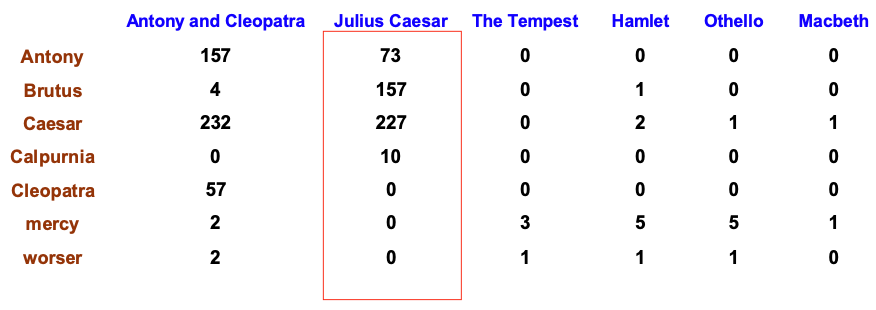
Term frequency tf
Term frequency of term in document
We want to use tf when computing query-document match scores
Log-frequency weighting
- Log frequency weight of term in
- Score for a document-query pair: sum over terms in both and
Document frequency
💡 Rare terms are more informative than frequent terms
: Document frequency of
- The number of documents that contain
- Inverse measure of the informativeness of
: inverse document frequency of
(use instead of to “dampen” the effect of )
Collection frequency of : the number of occurrences of in the collection, counting multiple occurrences.
tf-idf weighting
The tf-idf weight of a term is the product of its tf weight and its idf weight
Best known weighting scheme in information retrieval
Increases with the number of occurrences within a document
Increases with the rarity of the term in the collection
Example
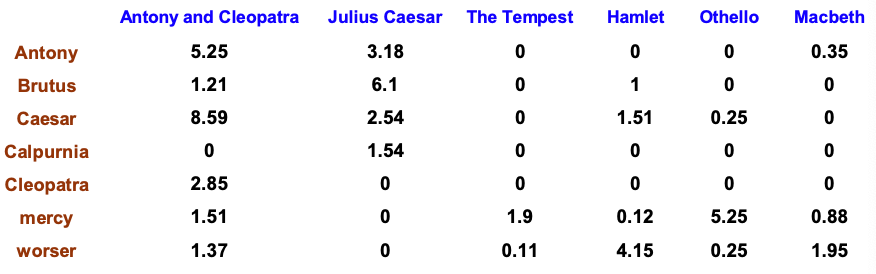
Each document is now represented by a real-valued vector of tf-idf weights
Documents as vectors
- -dimensional vector space
- Terms are axes of the space
- Documents are points or vectors in this space
- Very high-dimensional: tens of millions of dimensions when you apply this to a web search engine! 😱
- Very sparse vectors (most entries are zero)
- Distributional similarity based representations
- Get a lot of value by representing a word by means of its neighbors
- “You shall know a word by the company it keeps”
- Low dimensional vectors
- The number of topics that people talk about is small
- 💡Idea: store “most” of the important information in a fixed, small number of dimensions: a dense vector (Usually 25 – 1000 dimensions)
- Reduce the dimensionality: Go from big, sparse co-occurrence count vector to low dimensional “word embedding”
- Traditional Way: Latent Semantic Indexing/Analysis
- Use Singular Value Decomposition (SVD)
- Similarity is preserved as much as possible
- Traditional Way: Latent Semantic Indexing/Analysis
DL methods
Word representation in neural networks:
1-hot vector
Sparse representation
NN learn continuous dense representation
- Word embeddings
- End-to-End learning
- Pre-training using other task
- Word embeddings
Word embeddings
- Predict surrounding words
- E.g. Word2Vec, GloVe
- Document representation:
- TF-IDF Vectors: Sum of word vectors
- Word embeddings: Sum or average of word vectors
- 🔴 Problems
- High dimension
- Unseen words: Not possible to represent words not seen in training
- Morphology: No modelling of spelling similarity
Letter n-grams
- Mark begin and ending
- E.g.
#good#
- E.g.
- Letter tri-grams
- E.g.
#go,goo,ood,od#
- E.g.
- 🔴 Problem:
- Collision: Different words may be represented by same trigrams
Measure similarity
Rank documents according to their proximity to the query in this space
- proximity = similarity of vectors
- proximity ≈ inverse of distance
(Euclidean) Distance is a bad idea!
- Euclidean distance is large for vectors of different lengths
Use angle instead of distance
- 💡 Key idea: Rank documents according to angle with query.
From angles to cosines
As Cosine is a monotonically decreasing function for the interval
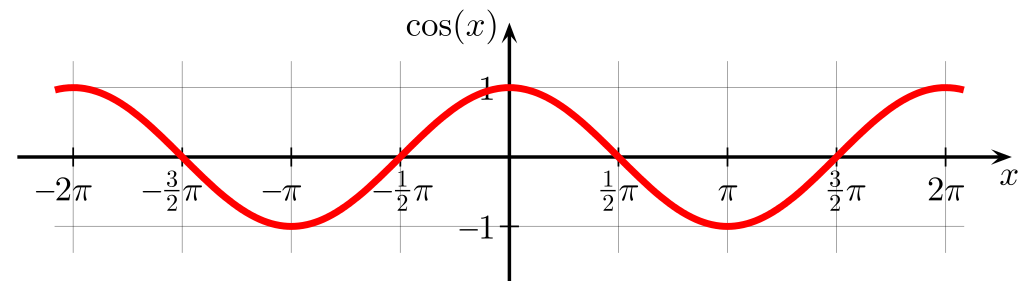
The following two notions are equivalent:
Rank documents in decreasing order of the angle between query and
document
Rank documents in increasing order of
Length normalization
Dividing a vector by its norm makes it a unit (length) vector (on
surface of unit hypersphere)
–> Long and short documents now have comparable weights
: e.g. the tf-idf weight of term i in the query
: e.g. the tf-idf weight of term i in the document
Illustration example

Link information
Hypertext and links
- Questions
- Do the links represent a conferral of authority to some pages? Is this useful for ranking?
- Application
The Web
Email
Social networks
Links
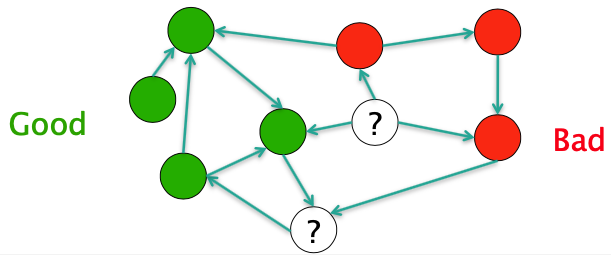
The Good, The Bad and The Unknown
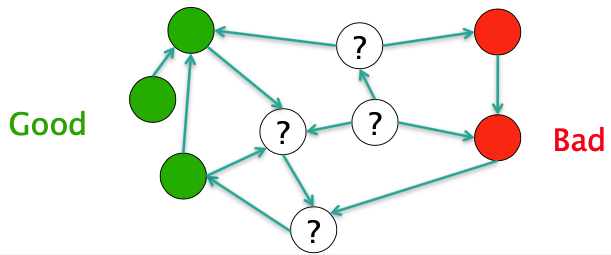
Good nodes won’t point to Bad nodes
All other combinations plausible
If you point to a Bad node, you’re Bad
If a Good node points to you, you’re Good
Web as a Directed Graph
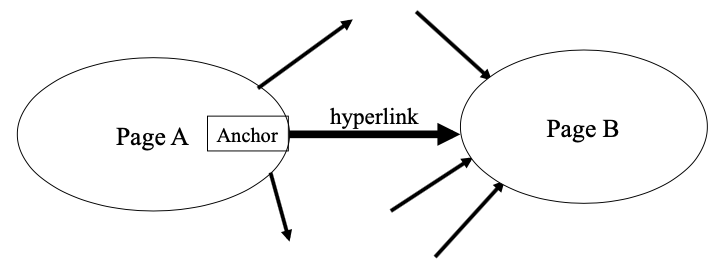
- Hypothesis 1: A hyperlink between pages denotes a conferral of authority (quality signal)
- Hypothesis 2: The text in the anchor of the hyperlink on page A describes the target page B
Anchor Text
Assumptions
reputed sites
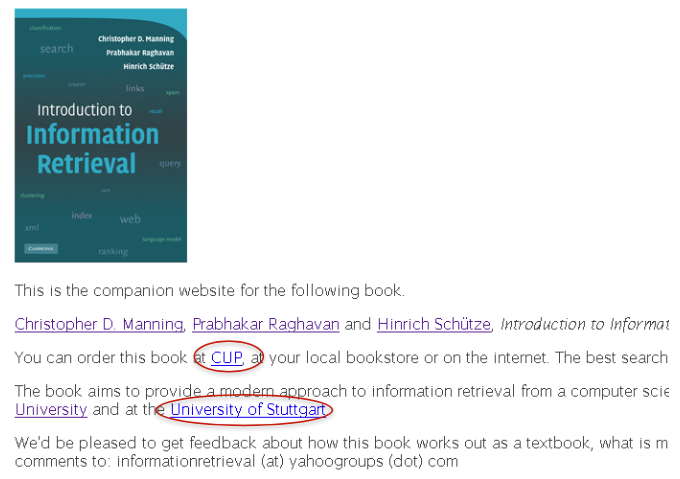
annotation of target
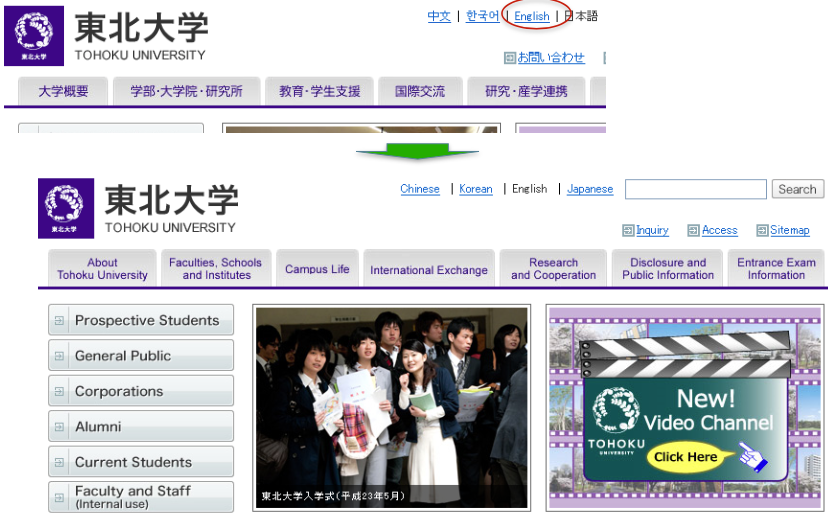
Indexing: When indexing a document D, include (with some weight) anchor text from links pointing to D.
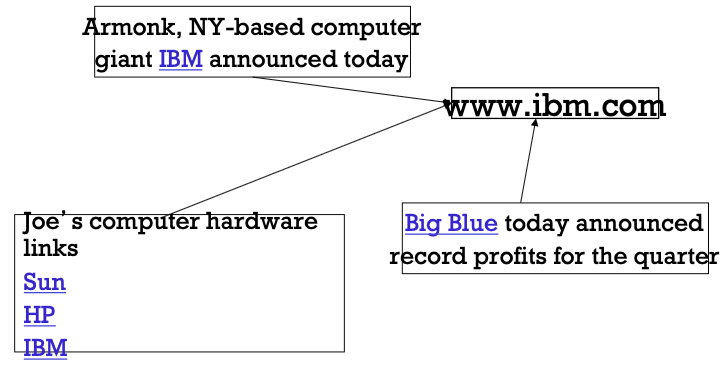 - Can sometimes have unexpected effects, e.g., spam, **miserable failure** 🤪
- Solution: score anchor text with weight depending on the **authority** of the anchor page’s website
- *E.g., if we were to assume that content from cnn.com or yahoo.com is authoritative, then trust (more) the anchor text from them*
- Can sometimes have unexpected effects, e.g., spam, **miserable failure** 🤪
- Solution: score anchor text with weight depending on the **authority** of the anchor page’s website
- *E.g., if we were to assume that content from cnn.com or yahoo.com is authoritative, then trust (more) the anchor text from them*
Link analysis: Pagerank
Citation Analysis
- Citation frequency
- Bibliographic coupling frequency: Articles that co-cite the same articles are related
- Citation indexing
Pagerank scoring
Imagine a user doing a random walk on web pages:
Start at a random page
At each step, go out of the current page along one on the links on that page, equiprobably
“In the long run” each page has a long-term visit rate - use this as the page’s score.
But the web is full of dead-ends.
Random walk can get stuck in dead-ends. 😢
Makes no sense to talk about long-term visit rates.
At a dead end, jump to a random web page.
At any non-dead end, with probability 10%, jump to a random web page.
Result of teleporting
- Now cannot get stuck locally.
- There is a long-term rate at which any page is visited