Evaluation

Two classes

Gold labels

the human-defined labels for each document that we are trying to match

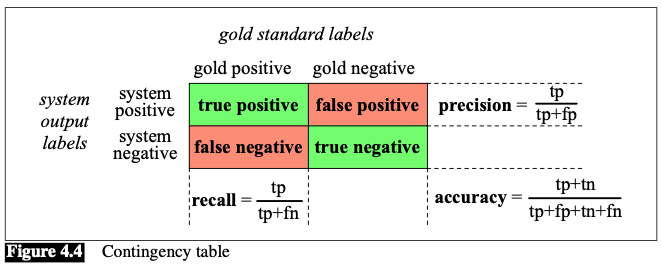
Confusion Matrix

To evaluate any system for detecting things, we start by building a Contingency table (Confusion matrix):

Evaluation metric

• Accuracy

  $$ \text{Accuracy} = \frac{\text{tp+tn}}{\text{tp+fp+tn+fn}} $$
  • doesn’t work well when the classes are unbalanced 🤪

• Precision (P)

  • measures the percentage of the items that the system detected (i.e., the system labeled as positive) that are in fact positive (i.e., are positive according to the human gold labels). $$ \text{Precision} = \frac{\text{tp}}{\text{tp+fp}} $$

• Recall (R)

  • measures the percentage of items actually present in the input (i.e., are positive according to the human gold labels) that were correctly identified by the system (i.e., the system labeled as positive). $$ \text{Recall} = \frac{\text{tp}}{\text{tp+fn}} $$

• F-measure

  $$ F_{\beta}=\frac{\left(\beta^{2}+1\right) P R}{\beta^{2} P+R} $$

  • $\beta$: differentially weights the importance of recall and precision, based perhaps on the needs of an application

    • $\beta > 1$: favor recall

    • $\beta < 1$: favor precision

    • $\beta = 1$: precision and recall are equally balanced (the most frequently used metric)

      $$ F_{1}=\frac{2 P R}{P+R} $$

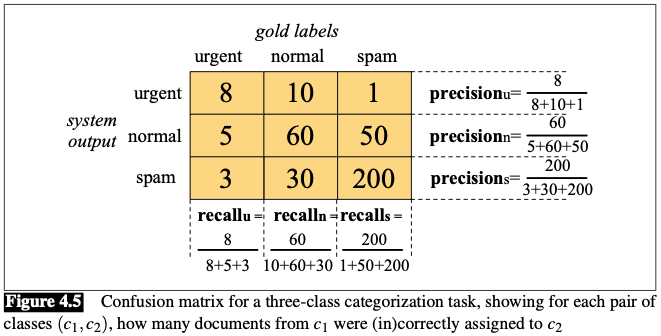
More than two classes

Solution: one-of or multinomial classification

• The classes are mutually exclusive and each document or item appears in exactly ONE class.
• How it works?
  • We build a separate binary classifier trained on positive examples from $c$ and negative examples from all other classes.
  • Given a test document or item $d$, we run all the classifiers and choose the label from the classifier with the highest score.

E.g.:

Evaluation metric:

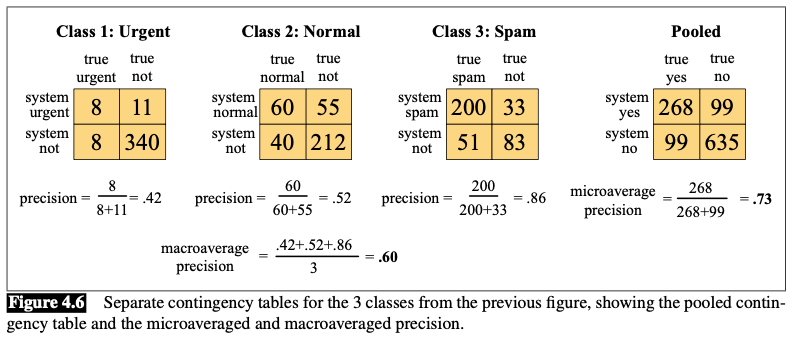
• Macroaveraging
  1. compute the performance for each class
  2. then average over classes
• Microaveraging
  1. collect the decisions for all classes into a single contingency table
  2. then compute precision and recall from that table.

E.g.: