Naive Bayes Classifiers

Notation

Classifier for text classification

• Input: $d$ (“document”)

• Output: $c$ (“class”)

• Training set: $N$ documents that have each been hand-labeled with a class $(d_1, c_1), \dots, (d_N, c_N)$

• 🎯 Goal: to learn a classifier that is capable of mapping from a new document $d$ to its correct class $c\in C$

• Type:

  • Generative:
    • Build a model of how a class could generate some input data
    • Given an observation, return the class most likely to have generated the observation.
    • E.g.: Naive Bayes
  • Discriminative
    • Learn what features from the input are most useful to discriminate between the different possible classes
    • Often more accurate and hence more commonly used
    • E.g.: Logistic Regression

Bag-of-words Representation

We represent a text document as if were a bag-of-words

• unordered set of words
• position ignored
• keeping only their frequency in the document

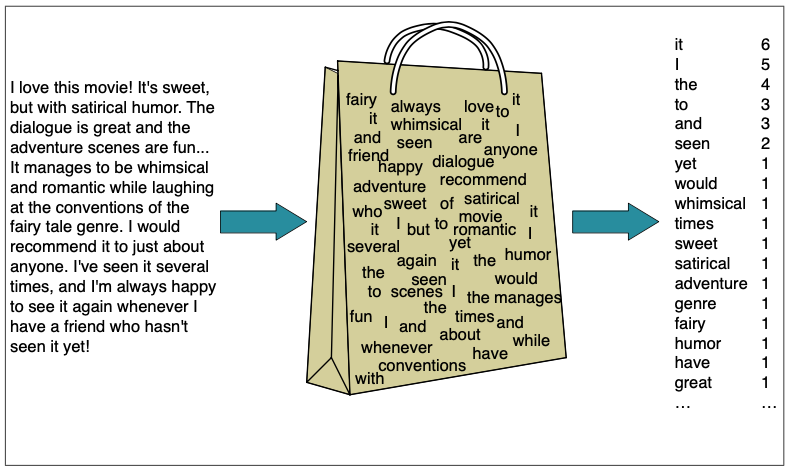
In the example in the figure, instead of representing the word order in all the phrases like “I love this movie” and “I would recommend it”, we simply note that the word I occurred 5 times in the entire excerpt, the word it 6 times, the words love, recommend, and movie once, and so on.

Naive Bayes

• Probablistic classifier

  • for a document $d$, out of all classes $c \in C$, the classifier returns the class $\hat{c}$ which has the maximum a-posterior probability (MAP) given the document

    

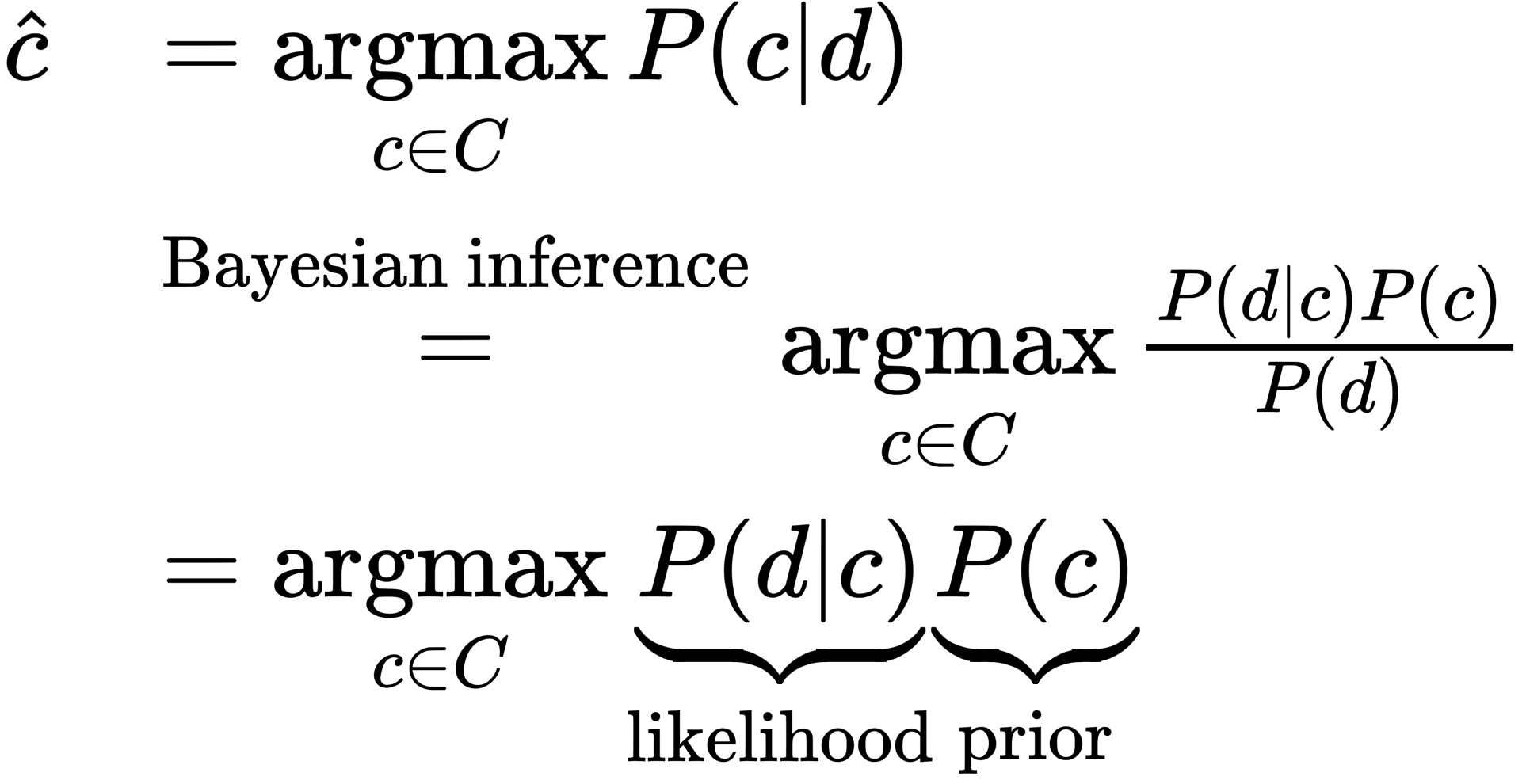
We represent a document $d$ as a set of features $f_1, f_2, \dots, f_n$, then

In order to make it possible to compute directly, Naive Bayes classifiers make two simplifying assumptions

• Bag-of-words assumption

  • we assume position does NOT matter, and that the word “love” has the SAME effect on classification whether it occurs as the 1st, 20th, or last word in the document.
  • Thus we assume that the features $f_1, f_2, \dots, f_n$ only encode word identity and not position.

• Naive Bayes assumption

  • The conditional independence assumption that the probabilities $P(f_i|c)$ are independent given the class $c$ and hence can be ‘naively’ multiplied $$P\left(f_{1}, f_{2}, \ldots ., f_{n} | c\right)=P\left(f_{1} | c\right) \cdot P\left(f_{2} | c\right) \cdot \ldots \cdot P\left(f_{n} | c\right)$$

Based on these two assumptions, the final equation for the class chosen by a naive Bayes classifier is thus

To apply the naive Bayes classifier to text, we need to consider word positions, by simply walking an index through every word position in the document:

To avoid underflow and increase speed, Naive Bayes calculations, like calculations for language modeling, are done in log space: