PyTorch Tensor

PyTorch Tensor

import torch

The world as floating-point numbers

Neural networks transform floating-point representations into other floating- point representations. The starting and ending representations are typically human interpretable, but the intermediate representations are less so.

To handle and store data, PyTorch introduces a undamental data structure: the tensor. In the context of deep learning, tensors refer to the generalization of vectors and matrices to an arbitrary number of dimensions

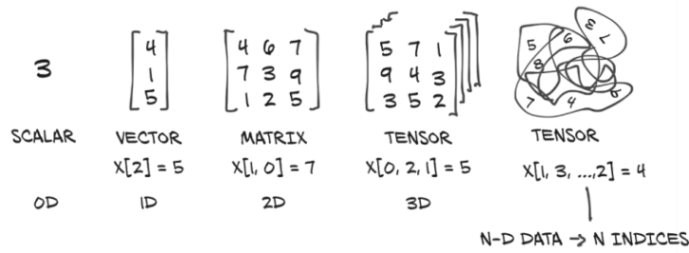
Tensors: Multidimensional arrays

Another name for tensor is multidimensional array. Compared to NumPy arrays, PyTorch tensors have a few superpowers, such as

the ability to perform very fast operations on graphical processing units (GPUs)
distribute operations on multiple devices or machines
keep track of the graph of computations that created them.

Tensor construction

From python list:

a = torch.tensor(list(range(9)))
a

tensor([0, 1, 3, 3, 4, 5, 6, 7, 8])

Use constuctors from PyTorch

a = torch.ones(3, 4)
a

tensor([[1., 1., 1., 1.],
        [1., 1., 1., 1.],
        [1., 1., 1., 1.]])

The essence of tensors

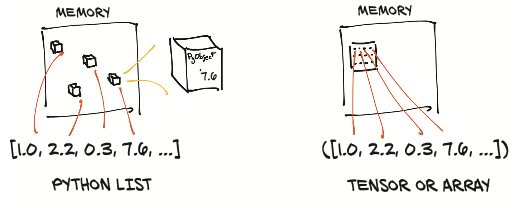
Python lists or tuples of numbers are collections of Python objects that are individually allocated in memory.
PyTorch tensors or NumPy arrays are views over (typically) contiguous memory blocks containing unboxed C numeric types rather than Python objects.

Indexing tensors

Use range indxing notation just as in standard python lists.

Tensor element types

Specifying the numeric type with `dtype`

The dtype argument to tensor constructors (that is, functions like tensor, zeros, and ones) specifies the numerical data (d) type that will be contained in the tensor. The default data type for tensors is 32-bit floating-point.

E.g.

double_points = torch.ones(10, 2, dtype=torch.double)

Typical `dtype`

Computations happening in neural networks typically executed with 32-bit floating-point precision.
Tensors can be used as indexes in other tensors. In this case, PyTorch expects indexing tensors to have a 64-bit integer (int64) data type.
Predicates on tensors, such as points > 1.0, produce bool tensors indicating whether each individual element satisfies the condition.

Casting `dtype`

Cast the tensor to the right type using the corresponding casting method.

For example, cast torch.int to torch.double

points = torch.zeros(10, 2, dtype=torch.int)
points = points.double()

Or use the more convenient to method:

points = points.to(torch.double)

When mixing input types in operations, the inputs are converted to the larger type automatically.

The Tensor API

First, the vast majority of operations on and between tensors are available in the torch module and can also be called as methods of a tensor object. There is no difference between the two forms; they can be used interchangeably.

Example:

a = torch.ones(3, 2)
a_transpose = torch.transpose(a, 0, 1) # call from the torch module
a.shape, a_transpose.shape

(torch.Size([3, 2]), torch.Size([2, 3]))

a = torch.ones(3, 2)
a_transpose = a.transpose(0, 1) # method of the tensor object
a.shape, a_transpose.shape

(torch.Size([3, 2]), torch.Size([2, 3]))

The online docs (http://pytorch.org/docs) are exhaustive and well organized, with the tensor operations divided into groups:

Creation ops: Functions for constructing a tensor, like ones and from_numpy
Indexing, slicing, joining, mutating ops: Functions for changing the shape, stride, or content of a tensor, like transpose
Math ops: Functions for manipulating the content of the tensor through computations
- Pointwise ops: Functions for obtaining a new tensor by applying a function to each element independently, like abs and cos
- Reduction ops: Functions for computing aggregate values by iterating through tensors, like mean, std, and norm
- Comparison ops: Functions for evaluating numerical predicates over tensors, like equal and max
- Spectral ops: Functions for transforming in and operating in the frequency domain, like stft and hamming_window
- Other operations: Special functions operating on vectors, like cross, or matrices, like trace
- BLAS and LAPACK operations—Functions following the Basic Linear Algebra Subprograms (BLAS) specification for scalar, vector-vector, matrix-vector, and matrix-matrix operations
Random sampling: Functions for generating values by drawing randomly from probability distributions, like randn and normal
Serialization: Functions for saving and loading tensors, like load and save
Parallelism: Functions for controlling the number of threads for parallel CPU execution, like set_num_threads

Tensors: Scenic views of storage

Values in tensors are allocated in contiguous chunks of memory managed by torch.Storage instances.

A storage is a one-dimensional array of numerical data: that is, a contiguous block of memory containing numbers of a given type
A PyTorch Tensor instance is a view of such a Storage instance that is capable of indexing into that storage using an offset and per-dimension strides.

Multiple tensors can index the same storage even if they index into the data differently. For example:

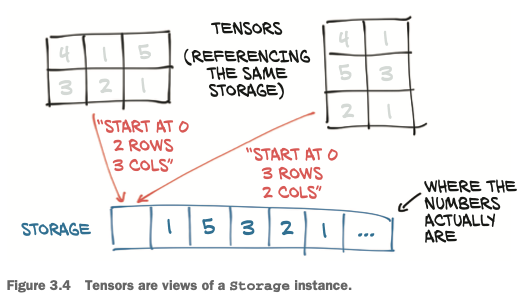
The underlying memory is allocated only once. So creating alternate tensor-views of the data can be done quickly regardless of the size of the data managed by the Storage instance.👏

Indexing into `storage`

The storage for a given tensor is accessible using the .storage property:

points = torch.tensor([[4.0, 1.0], [5.0, 3.0], [2.0, 1.0]])
points.storage()

 4.0
 1.0
 5.0
 3.0
 2.0
 1.0
[torch.FloatStorage of size 6]

Even though the tensor reports itself as having three rows and two columns, the storage under the hood is a contiguous array of size 6. In this sense, the tensor just knows how to translate a pair of indices into a location in the storage.

Changing the value of a storage leads to changing the content of its referring tensor:

points

tensor([[4., 1.],
        [5., 3.],
        [2., 1.]])

points_storage[0] = 2.0 # change the value of an element of a storage
points

tensor([[2., 1.],
        [5., 3.],
        [2., 1.]])

Modifying stored values: In-place operations

Methods with trailing underscore in their name, like zero_, indicates that the method operates in place by modifying the input instead of creating a new output tensor and returning it.

Any method without the trailing underscore leaves the source tensor unchanged and instead returns a new tensor.

Example:

a = torch.ones(3, 2)
a

tensor([[1., 1.],
        [1., 1.],
        [1., 1.]])

a.zero_() # in-place zeroing a
a

tensor([[0., 0.],
        [0., 0.],
        [0., 0.]])

🧐 Tensor metadata: Size, offset, and stride

In order to index into a storage, tensors rely on a few pieces of information that, together with their storage, unequivocally define them:

size/shpae: a tuple indicating how many elements across each dimension the tensor represents.
(storage) offset: index in the storage corresponding to the first element in the tensor.
stride: number of elements in the storage that need to be skipped over to obtain the next element along each dimension.

Example:

points = torch.tensor([[4.0, 1.0], [5.0, 3.0], [2.0, 1.0]])
second_point = points[1]

Size/Shape
```
second_point.size()
second_point.shape
```
Offset
```
second_point.storage_offset()
```
Stride
```
second_point.stride()
```

This indirection between Tensor and Storage makes some operations inexpensive, like transposing a tensor or extracting a subtensor, because they do not lead to memory reallocations. 👍 Instead, they consist of allocating a new Tensor object with a different value for size, storage offset, or stride.

Cloning a tensor

Use .clone()
Changing the cloned tensor won’t change the original tensor

Transposing without copying

For two-dimensional tensors, we can use t function, a a shorthand alternative to transpose

points = torch.tensor([[3, 1, 2], [4, 1, 7]]) 
points

tensor([[3, 1, 2],
        [4, 1, 7]])

points_t = points.t()
points_t

tensor([[3, 4],
        [1, 1],
        [2, 7]])

These two tensors share the same storage

id(points.storage()) == id(points_t.storage())

True

They differ only in shape and stride:
- Increasing the first index by one in points—for example, going from points [0,0] to points [1,0]—will skip along the storage by two elements; while increasing the second index—from points [0,0] to points [0,1]—will skip along the storage by one. (In other words, the storage holds the elements in the tensor sequentially row by row.)
```
points.shape, points.stride()
```
```
(torch.Size([2, 3]), (3, 1))
```
The transpose from points into points_t looks like this:
We change the order of the elements in the stride. After that, increasing the row (the first index of the tensor) will skip along the storage by one, just like when we were moving along columns in points.
```
points_t.shape, points_t.stride()
```
```
(torch.Size([3, 2]), (1, 3))
```
This is the very definition of transposing. No new memory is allocated: transposing is obtained only by creating a new Tensor instance with different stride ordering than the original.

Transposing in higher dimensions

We can transpose a multidimensional array by specifying the two dimensions along which transposing should occur:

some_t = torch.ones(3, 4, 5)
some_t.shape

torch.Size([3, 4, 5])

transpose_t = some_t.transpose(0, 2)
transpose_t.shape

torch.Size([5, 4, 3])

Moving tensors between CPU and GPU

Managing a tensor’s `device` attribute

Create a tensor on the GPU by specifying the corresponding argument to the constructor:

# create a tensor on the GPU 
points_gpu = torch.tensor([[4.0, 1.0], [5.0, 3.0], [2.0, 1.0]], device='cuda')

Move tensor between CPU and GPU using the to method:

points = torch.tensor([[3, 1, 2], [4, 1, 7]]) # tensor on CPU
points_gpu = points.to(device='cuda') # copy the tensor from CPU to GPU

points_cpu = points_gpu.to(device='cpu') #  copy the tensor from GPU to CPU

If our machine has more than one GPU, we can also decide on which GPU we allocate the tensor by passing a zero-based integer identifying the GPU on the machine
```
point_gpu = points.to(device='cuda:0')
```

We can also use the shorthand methods cpu and cuda instead of the to method to achieve the same goal:

a = torch.ones(3, 2)

a_gpu = a.cuda() # cpu -> gpu(cuda:0)
a_gpu = a.cuda(0) # explicitly specify which GPU
a_cpu = a_gpu.cpu() # gpu -> cpu

NumPy interoperability

PyTorch tensors can be converted to NumPy arrays and vice versa very efficiently:

Pytorch tensor –> Numpy array: numpy()

points = torch.ones(3, 4) # pytorch tensor
points

tensor([[1., 1., 1., 1.],
        [1., 1., 1., 1.],
        [1., 1., 1., 1.]])

points_np = points.numpy() # numpy array
points_np

array([[1., 1., 1., 1.],
       [1., 1., 1., 1.],
       [1., 1., 1., 1.]], dtype=float32)

‼️ Note:

The returned array shares the same underlying buffer with the tensor storage. This means the numpy method can be effectively executed at basically no cost, as long as the data sits in CPU RAM.
It also means modifying the NumPy array will lead to a change in the originating tensor. If the tensor is allocated on the GPU, PyTorch will make a copy of the content of the tensor into a NumPy array allocated on the CPU.
```
points_np[0][1] = 2 # changing an element of np array will also change tensor
points
```
```
tensor([[1., 2., 1., 1.],
        [1., 1., 1., 1.],
        [1., 1., 1., 1.]])
```

Numpy array –> Pytorch tensor: from_numpy()

points = torch.from_numpy(points_np)
points

tensor([[1., 2., 1., 1.],
        [1., 1., 1., 1.],
        [1., 1., 1., 1.]])

It aso use thesaem buffer-sharing strategy. I.e. Modifying the PyTorch tensor will lead to a change in the originating Numpy array:

points[1][1] = 3 # change element of tensor will also change np array
points_np

array([[1., 2., 1., 1.],
       [1., 3., 1., 1.],
       [1., 1., 1., 1.]], dtype=float32)

Serializing tensors

If the data inside is valuable, we will want to save it to a file and load it back at some point. After all, we don’t want to have to retrain a model from scratch every time we start running our program.

PyTorch uses pickle under the hood to serialize the tensor object, plus dedicated serialization code for the storage.

Save points tensor to an ourpoints.t file

# assuming the PATH variable holds the path of ourpoints.t file

torch.save(points, PATH)

Load points back:
```
points = torch.load(PATH)
```

Last updated on 2024-09-05

← Pretrained Networks 2020-10-18

Real-world Data Representation Using Tensors 2020-10-21 →

The world as floating-point numbers

Tensors: Multidimensional arrays

Tensor construction

The essence of tensors

Indexing tensors

Tensor element types

Specifying the numeric type with dtype

Typical dtype

Casting dtype

The Tensor API

Tensors: Scenic views of storage

Indexing into storage

Modifying stored values: In-place operations

🧐 Tensor metadata: Size, offset, and stride

Cloning a tensor

Transposing without copying

Transposing in higher dimensions

Moving tensors between CPU and GPU

Managing a tensor’s device attribute

NumPy interoperability

Serializing tensors

Specifying the numeric type with `dtype`

Typical `dtype`

Casting `dtype`

Indexing into `storage`

Managing a tensor’s `device` attribute