Big O Notation
Definition
In general, a better algorithm means a FASTER algorithm. In other words, it costs less runtime or it has lower time complexity.
Big O notation is one of the most fundamental tools to analyze the cost of an algorithm. It is about finding an asymptotic upper bound of the time complexity of an algorithm. I.e., Big O notation is about the worst-case scenario.
Basically, it answers the question: “How the runtime of an algorithm grows as the input grow?”
Rule of Thumbs
Different steps get added
Example
def func():
step1() # O(a)
step2() # O(b)
Overall complexity is $O(a + b)$
Constants do NOT matter
Constant are inconsequential, when input size $n$ is getting massively huge.
Example
- $O(2n) = O(n)$
- $O(500) = O(1)$
Different inputs $\Rightarrow$ different variables
Example
def intersection_size(list_A, list_B):
# Assumes that len(list_A) is lenA, len(len_listB) is lenB
count = 0
for a in list_A:
for b in list_B:
if a == b:
count += 1
return count
Overall complexity is $O(\text{lenA} \times \text{lenB})$
Smaller terms do NOT matter
Smaller terms are non-dominant, when input size $n$ is getting massively huge.
Example
- $O(n + 100) = O(n)$
- $O(n^2 + 200n) = O(n^2)$
Shorthands
Arithmetric operations are constant
Variable assignment is constant
Accessing elements in an array (by index) or object (by key) is constant
In a loop:
$$ \text{overall complexity} = (\text{length of loop}) \times (\text{complexity inside of the loop}) $$
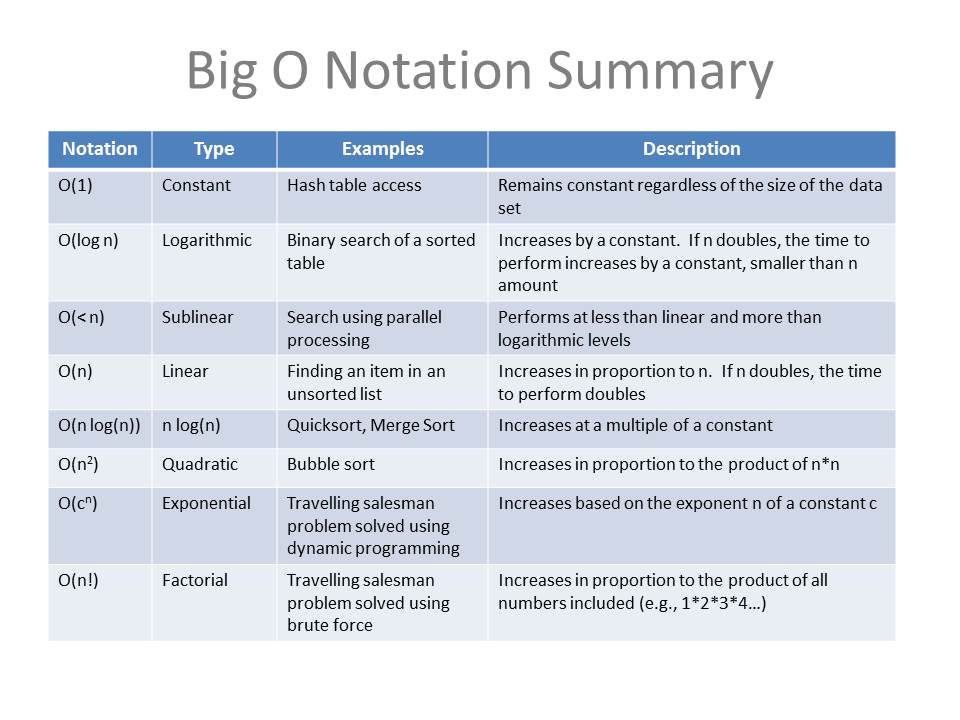
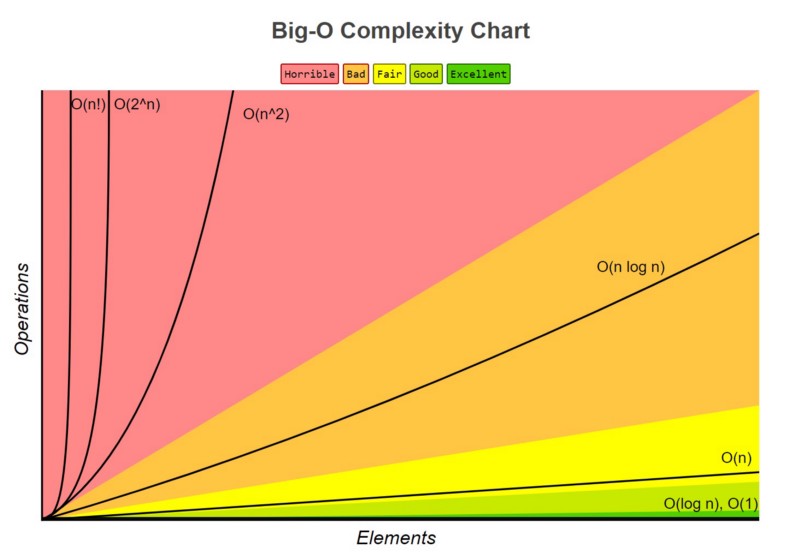
Summary of Complexity Classes
