Array and Linked List
TL;DR
| Array | Linked List | |
|---|---|---|
| Store in memory | Elements are stored in contiguous locations in memory. | Elements can be stored anywhere in memory |
| Size | Fixed, must be specified at the time of initialization | Changeable, can grow/shrink by insertion/deletion |
| Access element | Random access | Sequence access |
| Insert element | ||
| Delete element |
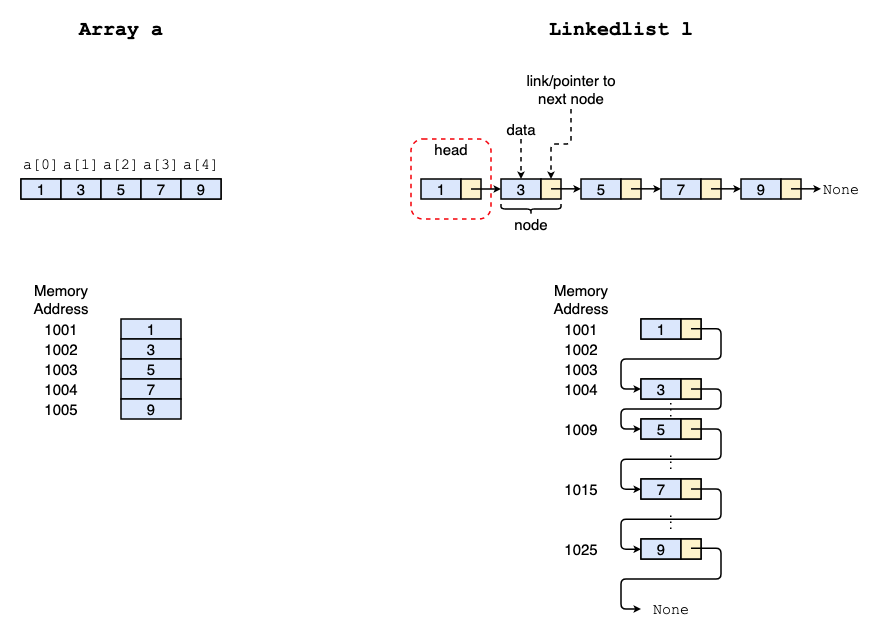
Storing In Memory
Array store elements in contiguous memory locations/blocks.
By Linked list, elements (also called nodes) can be stored anywhere in memory. Each node stores its next node’s address (link/pointer to next node).
Operations
Access
Array
Accessing an element in Array is simple. As array is essentially a block of continuous memory, we can directly access an element using index.
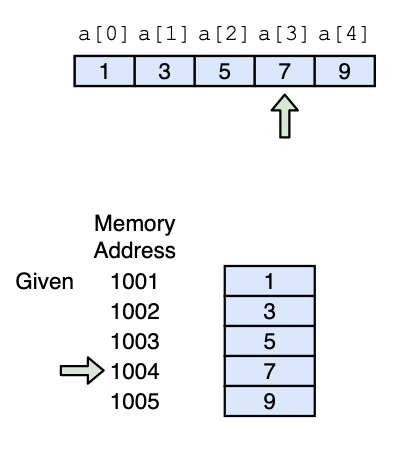
In other words, accessing an element in the array is independent of the size of the array. Hence, time complexity is .
Linked List
However, accessing a node in Linked list is not that easy. Since nodes are scattered out in memory, we have to traverse the linked list from the head node until we reach the target node.
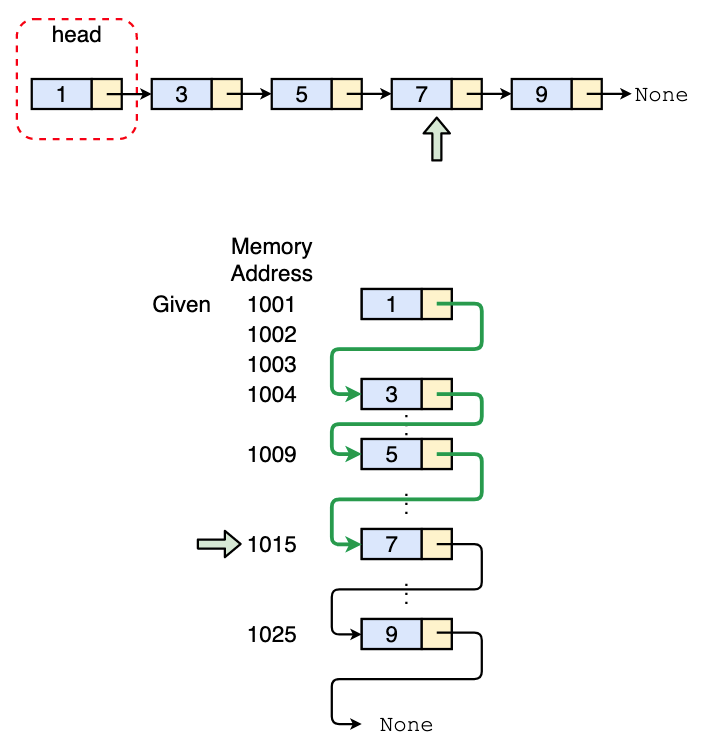
The worst case is that our target node is at the tail of the linked list. In this case we have to traverse the whole linked list. Time complexity is thus O(n).
Insert
Array
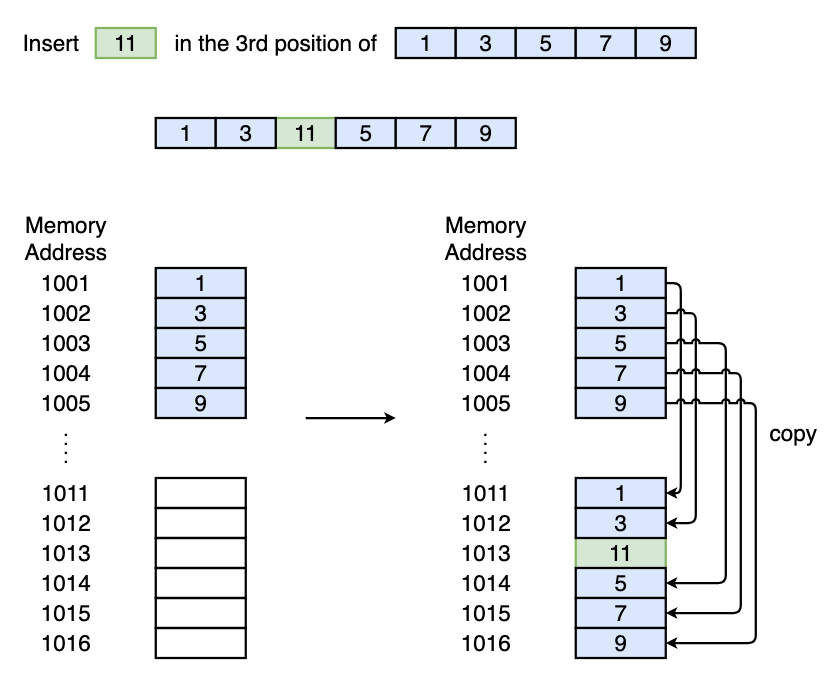
Inserting an element in the Array is a pain.
For example, we want to insert 11 in the 3rd position of array [1, 3, 5, 7, 9]. We need to
- allocate a new memory block of suitable size (in our case, 6),
- put new element
11in the 3rd position, and copy other elements to the right place.
Linked list
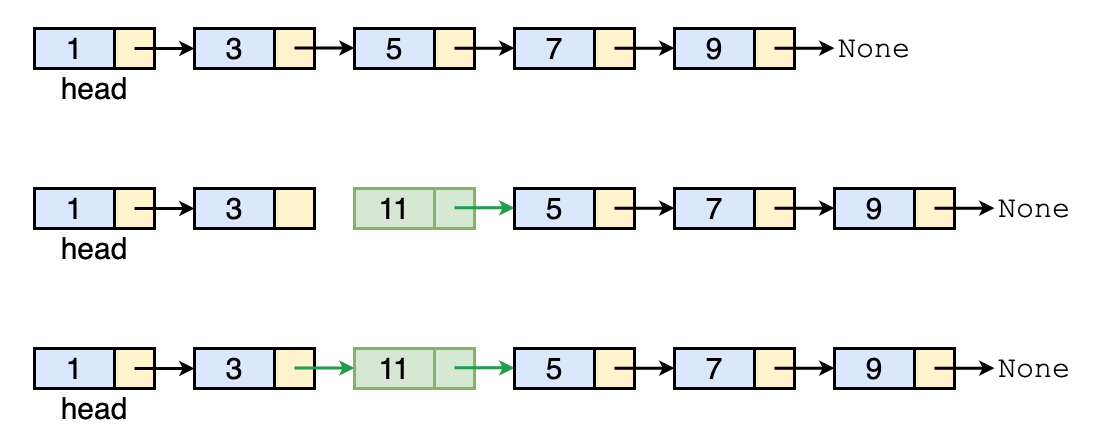
Key of insertion is to maintain the order/sequence of nodes using links.
Insert in the middle
Let’s say we want to insert a new_node between left_node and right_node.
Before insertion:
left_node --> right_node
After insertion, the linked should look like:
left_node --> new_node --> right_node
Keeping this in mind, we have the idea of insertion:
new_node.next = left_node.next
left_node.next = new_node
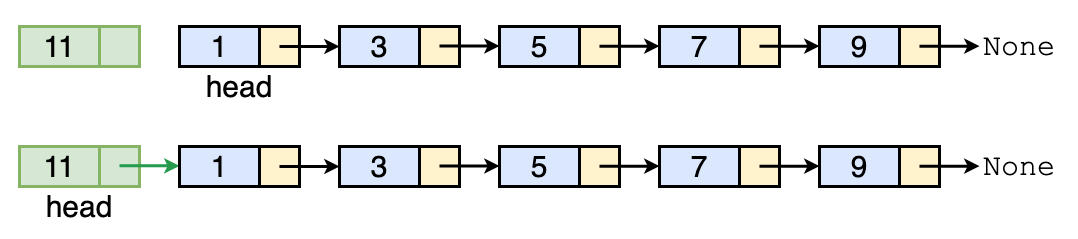
Insert at head
By inserting a new node at the head of linked list, we need to specify the new head after the insertion.
Assume that we want to insert new_node before linked_list.head:
new_node.next = linked_list.head
linked_list.head = new_node
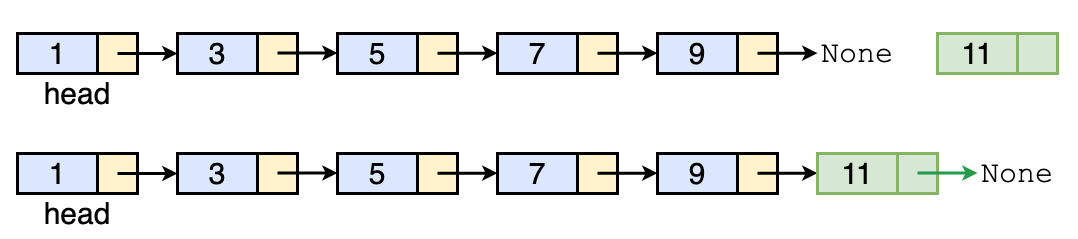
Insert at tail
By inserting a new node at the tail of linked list, we need to specify that the new node is the tail.
Assume that we want to insert new_node after tail_node.
Before insertion:
tail_node --> None
After insertion:
tail_node --> new_node --> None
Thus, the code of insertion should be:
# traverse linked list until reaching the tail node
tail_node.next = new_node
new_node.next = None
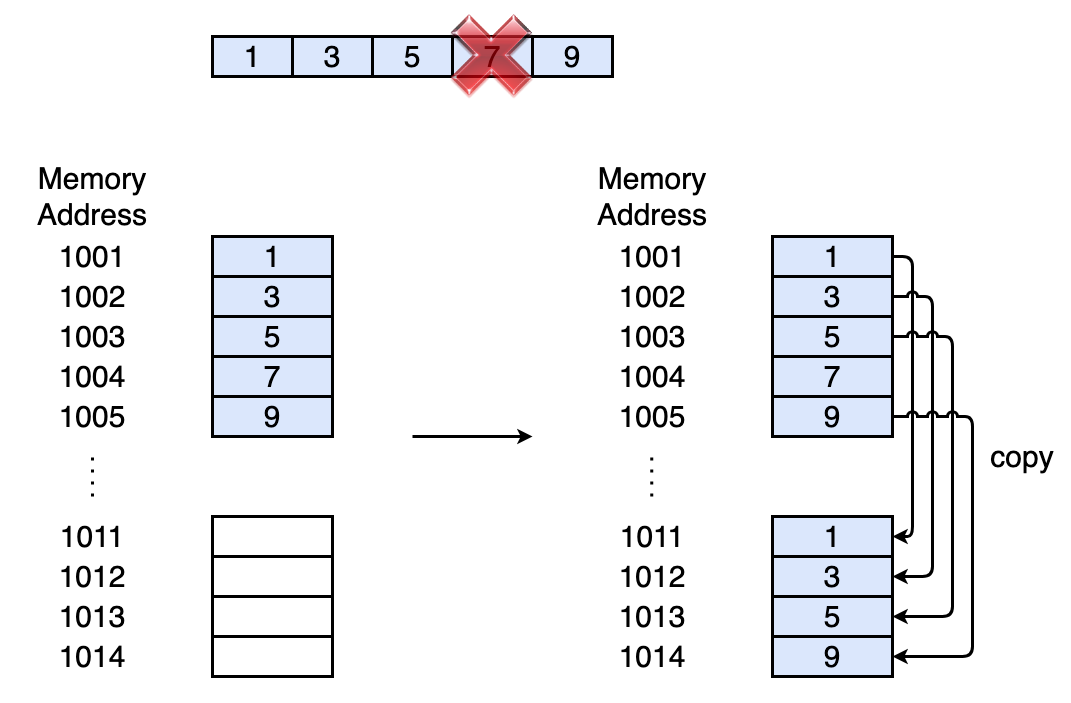
Delete
Array
Deleting of element from an array is similar to insertion. We need to allocate a new memory of suitable size, and copy remaining elements to the right place.
Linked list
Similar to insertion, we just need to maintain the order/sequence of nodes using links.
Insert a node in the middle
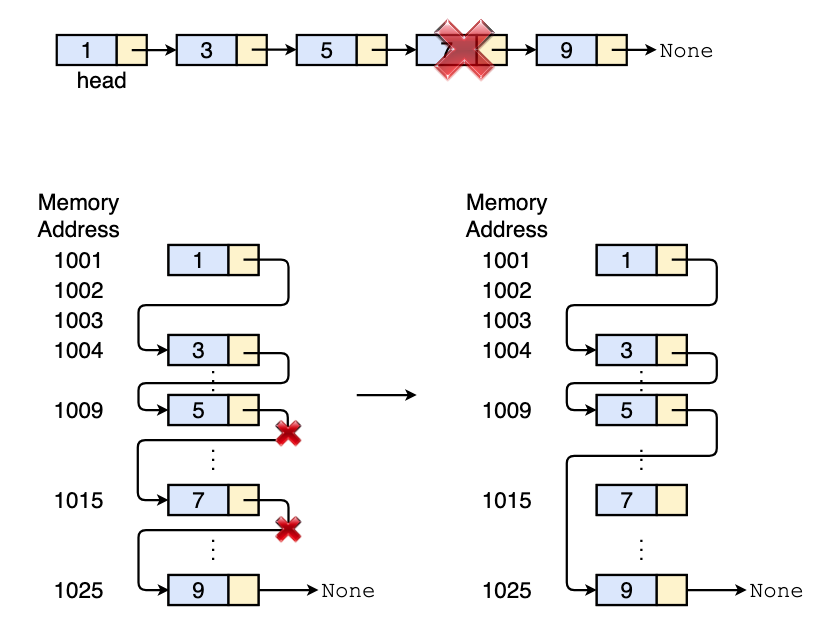
Let’s say we want to delete del_node between left_node and right_node.
Before deletion:
left_node --> del_node --> right_node
After deletion:
left_node --> right_node
Therefore, we just need to do the followings
left_node.next = right_node
Example:
Delete head node
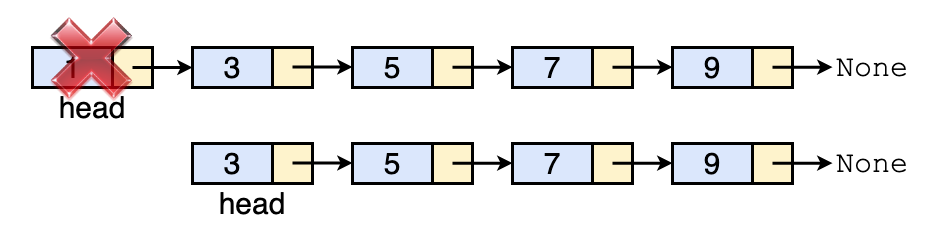
Let’s say we want to delete linked_list.head. After deletion, we need to announce that the new head is linked_list.head.next.
linked_list.head = linked_list.head.next
Delete tail node
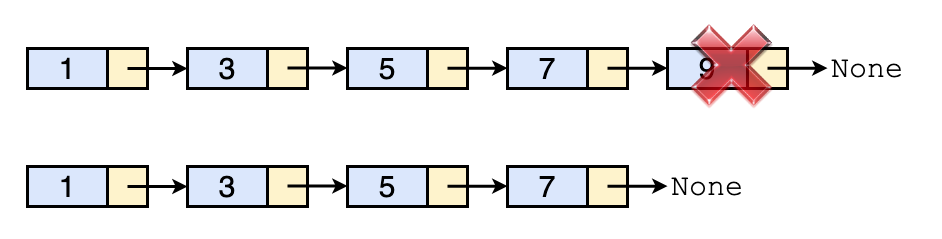
After deleting the tail node, the second last node becomes the new tail node.
Before deletion:
left_node --> tail_node --> None
After deletion:
left_node --> None
Therefore, we just need to do the followings
left_node.next = None
Array vs. Linked List
| Array | Linked List | |
|---|---|---|
| Access element | Fast | Slow |
| Insert element | Slow | Fast |
| Delete element | Slow | Fast |
- By frequent retrieval/accessing, use Array
- By frequent insertion/deletion, use Linked List
LinkedList in Python
Implement our own Linked List
To implement the linked list, we firstly need to implment a class for node, element of the list:
class Node:
def __init__(self, data):
self.data = data
self.next = None
def __repr__(self):
return self.data
Then we implment the linked list:
class LinkedList:
def __init__(self, data_list=None):
self.head = None
if data_list is not None:
node = Node(data=data_list.pop(0))
self.head = node
for element in data_list:
node.next = Node(data=element)
node = node.next
def __repr__(self):
node = self.head
nodes = list()
while node is not None:
nodes.append(node.data)
node = node.next
nodes.append("None")
return " -> ".join(nodes)
def __iter__(self):
node = self.head
while node is not None:
yield node
node = node.next
def add_first(self, new_node):
"""
Insert new_node at head
"""
new_node.next = self.head
self.head = new_node
def add_last(self, new_node):
"""
Insert new_node at tail
"""
# If linked list is empty,
# new node will be the only node in linked list,
# i.e. head and tail node are the same
if self.head is None:
self.head = new_node
return
# If linked list is not empty:
# 1. we need to traverse the whole list until we reach the current last node
# 2. we add the new node as the next node of the current last node
for current_node in self:
pass
current_node.next = new_node
def add_after(self, target_node_data, new_node):
"""
Insert new_node after the node whose data is target_node_data
"""
if self.head is None:
raise Exception("Linked list is empty.")
for node in self:
if node.data == target_node_data:
new_node.next = node.next
node.next = new_node
return
raise Exception(f"Node with data '{target_node_data}' not found.")
def remove_node(self, target_node_data):
"""
Remove node whose data is target_node_data
"""
# If linked list is empty, then raise an exception
if self.head is None:
raise Exception("Linked list is empty.")
# If the node to be removed is the current head,
# then we want the next node in the list to become the new head
if self.head.data == target_node_data:
self.head = self.head.next
return
# If list is not empty and node to be removed is not the current head,
# we traverse the list looking for the node to be removed.
# If we find it, then we need to update its previous node to point to its next node
previous_node = self.head
for node in self:
if node.data == target_node_data:
previous_node.next = node.next
return
previous_node = node
# If we traverse the whole list without finding the node to be removed,
# then raise an exception
raise Exception(f"Node with data '{target_node_data}' not found.")
Traverse
llist = LinkedList(["a", "b", "c", "d", "e"])
llist
a -> b -> c -> d -> e -> None
for node in llist:
print(node)
a
b
c
d
e
Insert
llist = LinkedList()
llist
None
Insert at head:
llist.add_first(Node("a"))
llist
a -> None
Insert at tail:
llist.add_last(Node("b"))
llist
a -> b -> None
llist.add_last(Node("d"))
llist
a -> b -> d -> None
Insert in the middle:
llist.add_after("b", Node("c"))
llist
a -> b -> c -> d -> None
Remove
llist = LinkedList(["a", "b", "c", "d", "e"])
llist
a -> b -> c -> d -> e -> None
Remove head:
llist.remove_node("a")
llist
b -> c -> d -> e -> None
Remove tail:
llist.remove_node("e")
llist
b -> c -> d -> None
Remove node in the middle:
llist.remove_node("c")
llist
b -> d -> None
Double-ended Queue (Deque)
collections.deque uses an implementation of a linked list in which you can access, insert, or remove elements from the beginning or end of a list with constant 𝑂(1) performance.
Append/Remove element from the right side:
append()/pop()Append/Remove element from the left side:
appendleft()/popleft()
Implment Queue using deque
For a queue, we use a First-In/First-Out (FIFO) approach. I.e., the first element inserted in the list is the first one to be retrieved.
queue = deque()
queue
deque([])
queue.append("Mary")
queue.append("John")
queue.append("Susan")
queue
deque(['Mary', 'John', 'Susan'])
Retrieve: (Order should be Mary --> John --> Susan)
queue.popleft()
'Mary'
queue.popleft()
'John'
queue.popleft()
'Susan'
Implment Stack using deque
For a stack, we use a Last-In/Fist-Out (LIFO) approach, meaning that the last element inserted in the list is the first to be retrieved.
queue = deque()
queue
deque([])
queue.append("Mary")
queue.append("John")
queue.append("Susan")
queue
deque(['Mary', 'John', 'Susan'])
Retrieve: (Order should be Susan --> John --> Mary)
queue.pop()
'Susan'
queue.pop()
'John'
queue.pop()
'Mary'