Merge Sort | Haobin Tan

Merge Sort

TL;DR

Merge sort use Divide and Conquer strategy
- Repeatedly divides the array into two subarrays until subarrays of size 1
- Merge two sorted array to achieve a bigger sorted array
Time complexity is $O(n \log n)$
Space complexity is $O(n)$ (non-inplace)

How Merge Sort Works?

Divide and Conquer Strategy

Merge Sort is one of the most popular sorting algorithms that is based on the principle of Divide and Conquer.

Using the Divide and Conquer technique, we divide a problem into subproblems. When the solution to each subproblem is ready, we “combine” the results from the subproblems to solve the main problem.

Suppose we had to sort an array arr. A subproblem would be to sort a sub-section of this array starting at index p and ending at index r, denoted as arr[p..r].

Divide
If q is the half-way point between p and r, then we can split the subarray arr[p..r] into two arrays arr[p..q] and arr[q+1, r].
Conquer
In the conquer step, we try to sort both the subarrays arr[p..q] and arr[q+1, r]. If we haven’t yet reached the base case, we again divide both these subarrays and try to sort them.
Combine
When the When the conquer step reaches the base step and we get two sorted subarrays arr[p..q] and arr[q+1, r] for array arr[p..r], we combine the results by creating a sorted array arr[p..r] from two sorted subarrays arr[p..q] and arr[q+1, r]

The MergeSort Algorithm

Repeatedly divides the array into two halves until we reach a stage where we try to perform MergeSort on a subarray of size 1 (the base case)
Combine the sorted arrays into larger sorted arrays until the whole array is merged.

Implementation

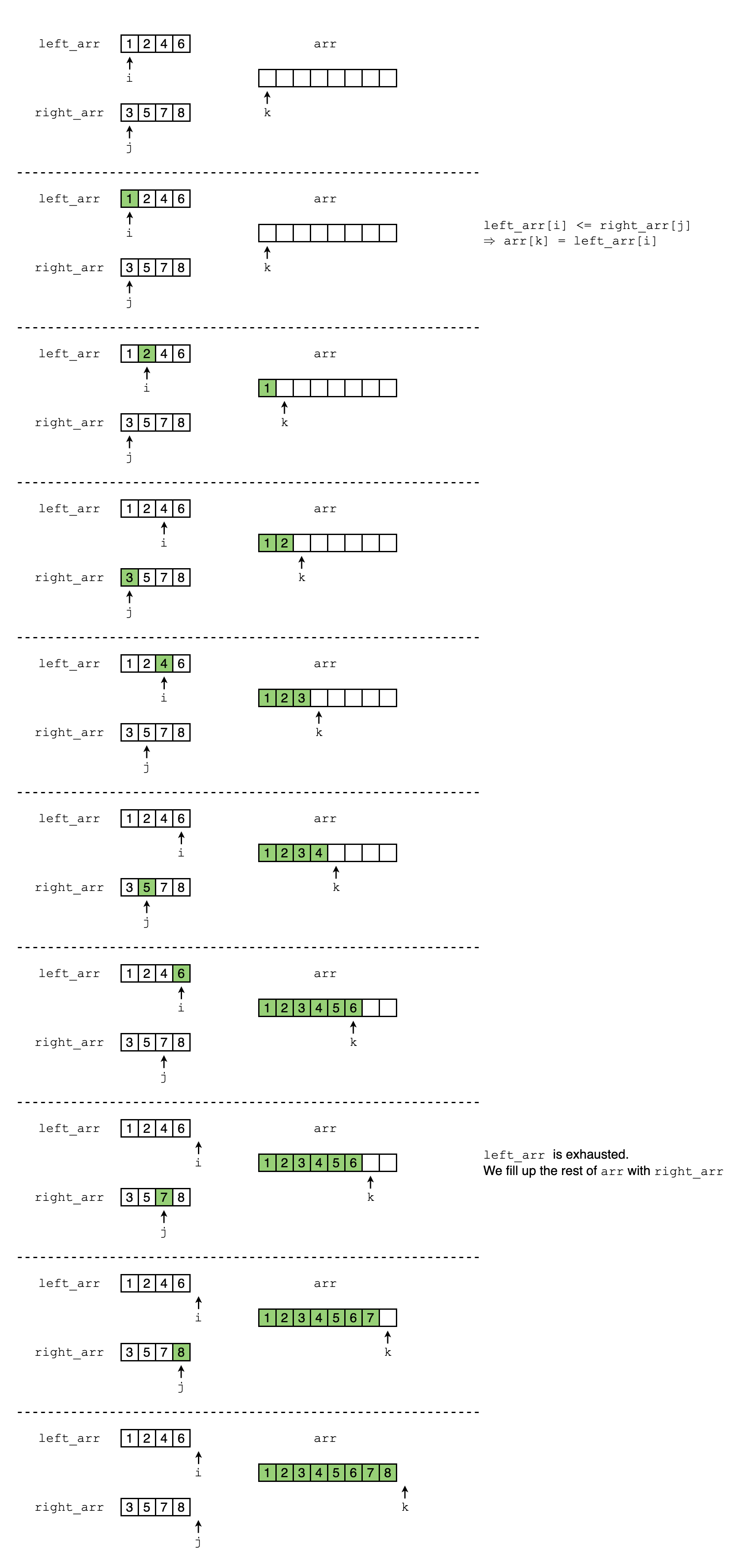
Merge: merge two sorted arrays to a larger sorted array

def merge(left_arr, right_arr, arr):
    """
    Merge left_arr and right_arr to arr.
    left_arr and right_arr are already sorted.
    After merging, arr should be sorted.
    """
    left_len = len(left_arr)
    right_len = len(right_arr)

    i = 0 # Mark the position of current smallest element in left_arr
    j = 0 # Mark the position of current smallest element in right_arr
    k = 0 # Mark the position to be filled in arr

    while (i < left_len and j < right_len): # left_arr and right_arr are not exhausted
        # We compare the current smallest elements of left_arr and right_arr,
        # fill arr with the smaller one
        if left_arr[i] <= right_arr[j]:
            arr[k] = left_arr[i]
            i += 1
        else:
            arr[k] = right_arr[j]
            j += 1

        k += 1
    
    if i > left_len - 1: 
        # left_arr is exhausted.
        # Thus, we fill up the rest of arr with right_arr
        arr[k:] = right_arr[j:]
    if j > right_len - 1: \
        # right_arr is exhausted
        # Thus, we fill up the rest of arr with left_arr
        arr[k:] = left_arr[i:]
    
    return arr

arr = [2, 4, 1, 6, 8, 5, 3, 7]
left_arr = [1, 2, 4, 6]
right_arr = [3, 5, 7, 8]
merge(left_arr, right_arr, arr)

[1, 2, 3, 4, 5, 6, 7, 8]

Merge sort

def merge_sort(arr):
    print(arr)
    
    # Base case
    if len(arr) < 2:
        return arr
    
    # Divide
    mid = len(arr) // 2
    left_arr = arr[:mid]
    right_arr = arr[mid:]

    # Conquer
    merge_sort(left_arr)
    merge_sort(right_arr)
    
    # Combine
    merge(left_arr, right_arr, arr)
    print(f"Merge {left_arr} and {right_arr} --> {arr}\n")

    return arr

arr = [2, 4, 1, 6, 8, 5, 3, 7]
print(merge_sort(arr))

[2, 4, 1, 6, 8, 5, 3, 7]
[2, 4, 1, 6]
[2, 4]
[2]
[4]
Merge [2] and [4] --> [2, 4]

[1, 6]
[1]
[6]
Merge [1] and [6] --> [1, 6]

Merge [2, 4] and [1, 6] --> [1, 2, 4, 6]

[8, 5, 3, 7]
[8, 5]
[8]
[5]
Merge [8] and [5] --> [5, 8]

[3, 7]
[3]
[7]
Merge [3] and [7] --> [3, 7]

Merge [5, 8] and [3, 7] --> [3, 5, 7, 8]

Merge [1, 2, 4, 6] and [3, 5, 7, 8] --> [1, 2, 3, 4, 5, 6, 7, 8]

[1, 2, 3, 4, 5, 6, 7, 8]