Quick Sort

TL;DR

• Divide and Conquer (D&C)
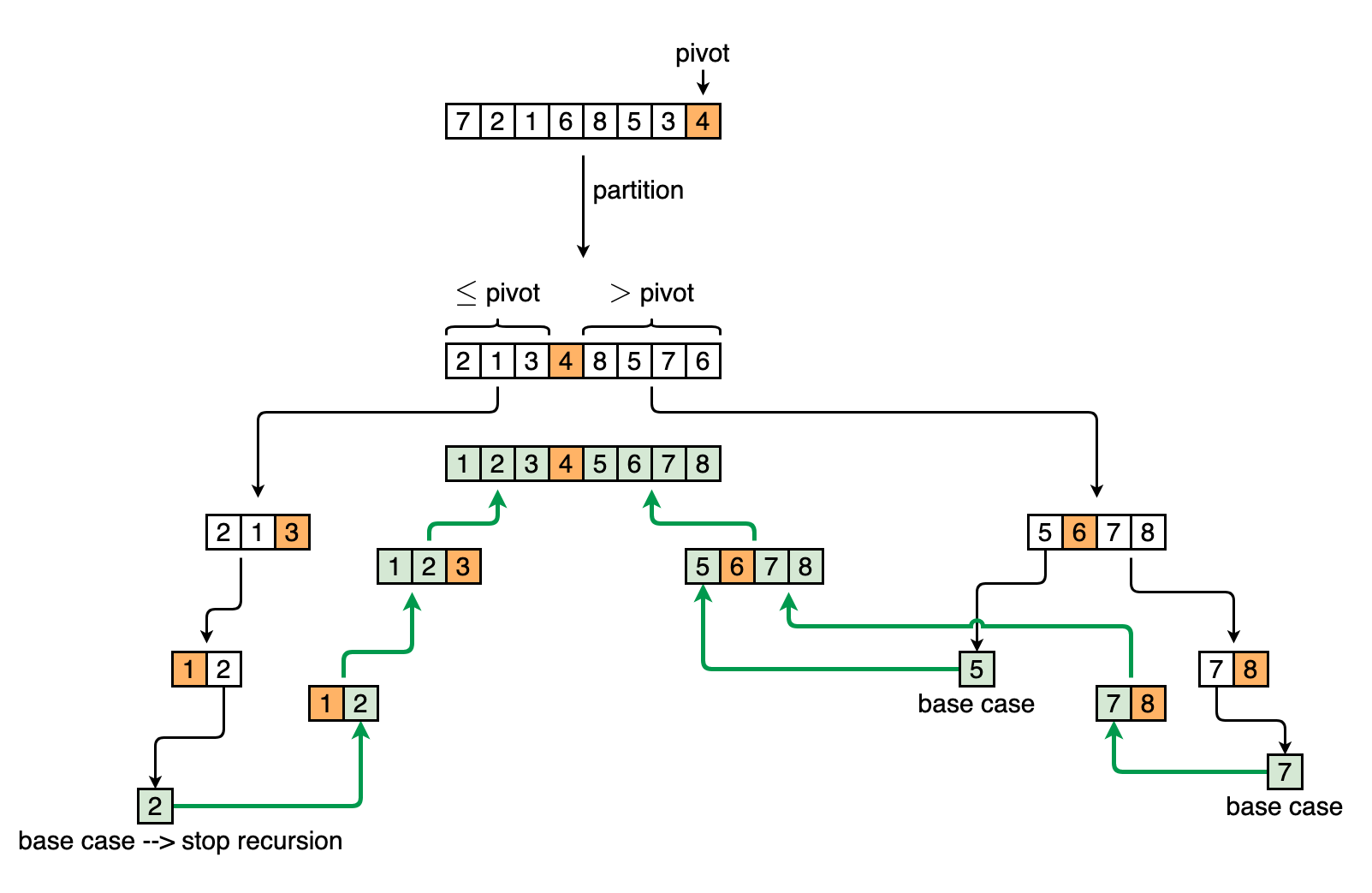
• Partition the array with the selected pivot: [elements <= pivot, pivot, elements > pivot]. Recursively apply quick sort on left and right sub-arrays.
• Average time complexity: $O(n \log n)$

💡 Idea

1. Pick a pivot
2. Partition the array into two sub-arrays
   • Elements less thant the pivot go to the left sub-array
   • Elements greater thant the pivot go to the right sub-array
3. Call quick sort recursively on the two sub-arrays
4. Concat left sub-array, pivot, and right sub-array

Implementation

Quick sort can be implemented using Divide and Conquer (D&C).

• Base case will be

  • Empty array
  • Array with just one element

  We can just return those arrays as is – there’s nothing to sort.

• Recursive case

  Decrease the array to two sub-arrays, apply quick sort on them, until they are decreased to base case.

Non In-place Implementation

In this version, we choose the first element as pivot.

def quick_sort(array):
    # base case
    if len(array) < 2:
        return array
    else:
        pivot = array[0] # choose the first element as pivot

        # Sub-array of all the elements less than the pivot
        less = [i for i in array[1:] if i <= pivot]

        # Sub-array of all the elements greater than the pivot
        greater = [i for i in array[1:] if i > pivot]

        return quick_sort(less) + [pivot] + quick_sort(greater)

In-place Implementation

To implement in-place quick sort, we won’t create any new array. Instead, we just swap the elements.

Here we will choose the last element as our pivot. In order to partition the array, we shift the elements which are less than pivot to the left, and shift the elements which are greater than pivot to the right.

def swap(arr, i, j):
    """
    Swap arr[i] and arr[j]
    """
    arr[i], arr[j] = arr[j], arr[i]

def partition(arr, start, end):
    """
    Partition the array with pivot.
    After partitioning, the array should look like 
    [elements <= pivot, pivot, elements > pivot]
    """
    pivot = arr[end]
    pivot_index = start

    for i in range(start, end):
        print(f"i={i}, arr: {arr}, pivot_index: {pivot_index}")
        if arr[i] < pivot:
            swap(arr, i, pivot_index)
            pivot_index += 1
    swap(arr, pivot_index, end)
    
    return pivot_index

arr = [7, 2, 1, 6, 8, 5, 3, 4]
partition(arr, 0, len(arr)-1)
arr

i=0, arr: [7, 2, 1, 6, 8, 5, 3, 4], pivot_index: 0
i=1, arr: [7, 2, 1, 6, 8, 5, 3, 4], pivot_index: 0
i=2, arr: [2, 7, 1, 6, 8, 5, 3, 4], pivot_index: 1
i=3, arr: [2, 1, 7, 6, 8, 5, 3, 4], pivot_index: 2
i=4, arr: [2, 1, 7, 6, 8, 5, 3, 4], pivot_index: 2
i=5, arr: [2, 1, 7, 6, 8, 5, 3, 4], pivot_index: 2
i=6, arr: [2, 1, 7, 6, 8, 5, 3, 4], pivot_index: 2
[2, 1, 3, 4, 8, 5, 7, 6]

With the implementation of partition(), in-place quick sort is simple:

def quick_sort_inplace(arr, start, end):
    # If start >= end, that means array is empty or contains only one element, which is the base case.
    # We do NOT need to sort the array, just keep it as it is.

    # If start < end, the array contains more than 1 element, which is the recursive case.
    if start < end:
        
        # Partition the array with pivot.
        pivot_index = partition(arr, start, end)

        # Recursively apply quick sort on the left sub-array ([elements <= pivot]) 
        quick_sort_inplace(arr, start, pivot_index-1)

        # Recursively apply quick sort on the right sub-array ([elements > pivot]) 
        quick_sort_inplace(arr, pivot_index+1, end)

arr = [7, 2, 1, 6, 8, 5, 3, 4]
quick_sort_inplace(arr, 0, len(arr)-1)
arr

[1, 2, 3, 4, 5, 6, 7, 8]

Complexity Analysis

Time Complexity

Quick sort is unique because its performance depends on the pivot choice.

• Worst case

  It occurs when the pivot element picked is either the greatest or the smallest element. This condition leads to the case in which the pivot element lies in an extreme end of the sorted array. One sub-array is always empty and another sub-array contains n - 1 elements. Thus, quicksort is called only on this sub-array.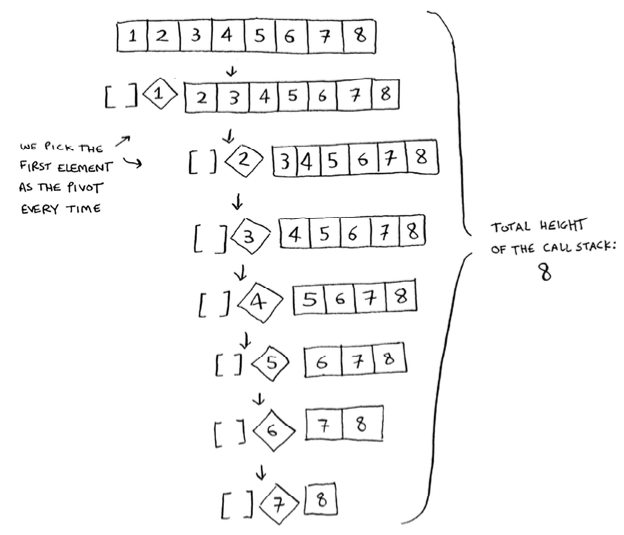

  

  Notice that we’re NOT splitting the array into two halves. Instead, one of the sub-arrays is always empty. So the call stack is really long. In this case, the stack size is $O(n)$.

• Best case

  The array is already sorted, and we always pick the middle element as the pivot.

  

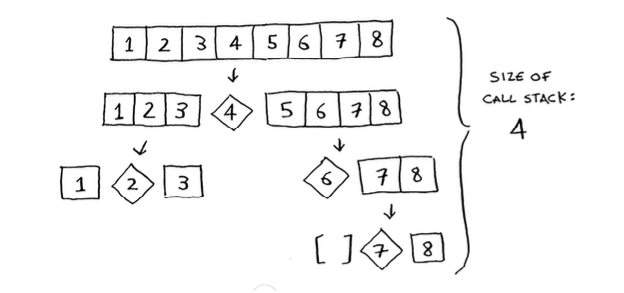
  In this case, the stack size is $O(\log n)$

On every level of the call stack, we “touch” $O(n)$ elements. So each level stack takes $O(n)$ time to complete.

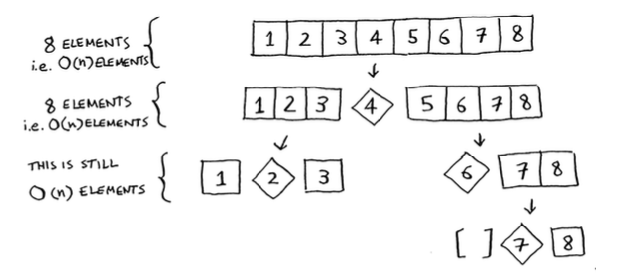
In our best case, there’re $O(\log n)$ levels. Each level takes $O(n)$ time. Therefore, time of the entire algorithm is

In the worst case, there are $O(n)$ levels, so the algorithm will take $O(n) \cdot O(n) = O(n^2)$ time.

Actually, the best case is also the average case. If we always choose a random element in the array as the pivot, quicksort will complete in $O(n \log n)$ time on average.

Space Complexity

The space complexity for quicksort is $O(\log n)$

Reference

Quicksort algorithm 👍