Docs
Notes
SI
Allgemeine Systeme
Abstraktion

Abstraktion

Skript 10.1, 10.2

Abstrahierte Systembeschreibung & Eigenschaften

Alle Komponenten eines Systems können durch

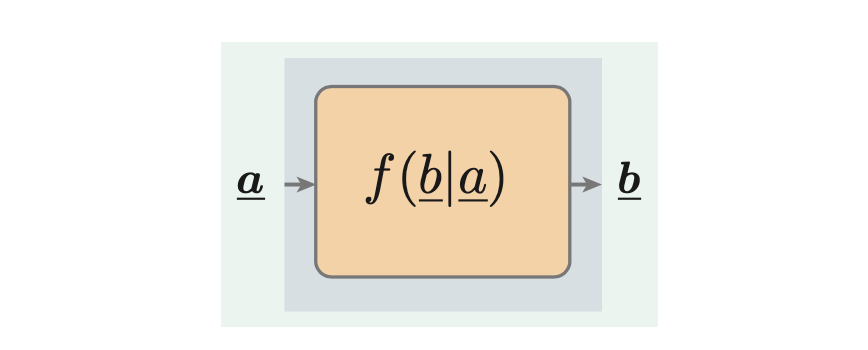
截屏2022-07-27 22.02.34

beschrieben werden (a‾∈RA,b‾∈Rb\underline{a} \in \mathbb{R}^A, \underline{b}\in \mathbb{R}^b ) .

Kauselität: aa (Grund) bewrikt bb (Wirkung).

Für a‾\underline{a} gegeben, f(b‾∣⋅)f(\underline{b} \mid \cdot) heißt Transitionsdichte.

Für b‾\underline{b} gegeben, f(⋅∣a‾)f(\cdot \mid \underline{a}) heißt Likelihood.

Eigenschaften von probabilistischer Systembeschreibung

In Allg. gilt

∫RBf(b‾∣a‾)db‾=1∀a‾ \int_{\mathbb{R}^{B}} f(\underline{b} \mid \underline{a}) d \underline{b}=1 \quad \forall \underline{a}

Es gilt aber i.A.

∫RAf(b‾∣a‾)da‾≠1, \int_{\mathbb{R}^{A}} f(\underline{b} \mid \underline{a}) d \underline{a} \neq 1,

sogar nicht definiert.

Vorwärts-/Rückwärtsinferenz

Vorwärtsinferenz

“Given information about a‾\underline{a}, we desire information about b‾\underline{b}.”

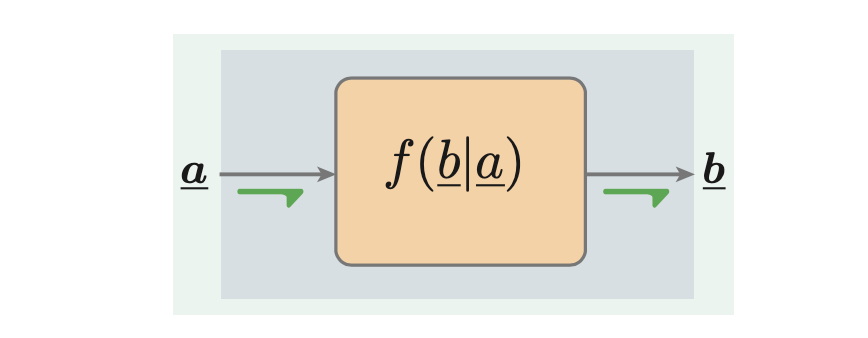
截屏2022-07-27 22.18.55
  • Gegeben: Werte für a^‾\underline{\hat{a}} oder Dichte f(a‾)f(\underline{a})
  • Gesucht: f(b‾)f(\underline{b})

Rückwärtsinferenz

“Information about the output b‾\underline{b} is given and we desire to reconstruct an appropriate description of a‾\underline{a}.”

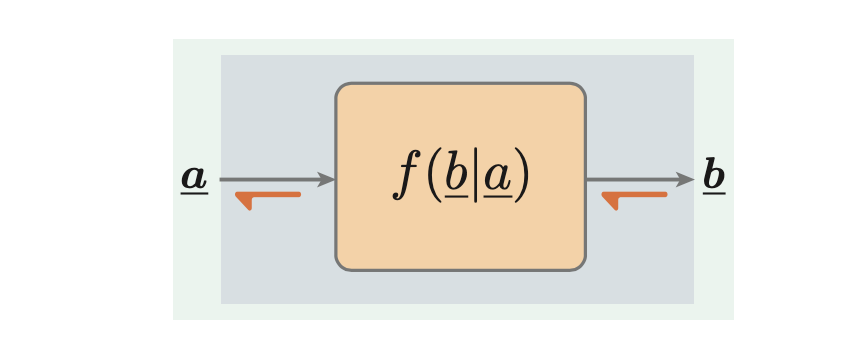
截屏2022-07-27 22.19.17
  • Gegeben: Werte für b^‾\underline{\hat{b}} oder Dichte f(b‾)f(\underline{b})
  • Gesucht: f(a‾)f(\underline{a})

Vorwärtsinferenz

Übungsblatt Aufg. 9.1

Annahme: KEIN Vorwissen über f(b‾)f(\underline{b})

Betrachte eine einfache generative Systemabbildung:

b‾=g‾(a‾)a‾∈RA,b‾∈RB \underline{b} = \underline{g}(\underline{a}) \quad \underline{a} \in \mathbb{R}^A, \underline{b} \in \mathbb{R}^B

Probablistische Systemabbildung:

f(b‾∣a‾)=δ(b‾−g‾(a‾)) f(\underline{b} \mid \underline{a}) = \delta(\underline{b} - \underline{g}(\underline{a}))

Marginalisierung ergibt:

f(b‾)=∫RAf(a‾,b‾)da‾=∫RAf(a‾∣b‾)f(a‾)da‾=∫RAδ(b‾−g‾(a‾))f(a‾)da‾ \begin{aligned} f(\underline{b}) &= \int_{\mathbb{R}^A} f(\underline{a}, \underline{b}) d\underline{a} \\\\ &= \int_{\mathbb{R}^A} f(\underline{a} \mid \underline{b}) f(\underline{a}) d\underline{a} \\\\ &= \int_{\mathbb{R}^A} \delta(\underline{b} - \underline{g}(\underline{a})) f(\underline{a}) d\underline{a} \end{aligned}

Weitere Vereinfachung NUR für konkrete g‾(⋅)\underline{g}(\cdot) möglich.

Für Speizialfall der Vorgabe eines Wertes a^‾\underline{\hat{a}} ergibt sich

f(a‾)=δ(a‾−a^‾) f(\underline{a}) = \delta(\underline{a} - \underline{\hat{a}})

Damit

f(b‾)=∫RAδ(b‾−g‾(a‾))f(a‾)da‾=∫RAδ(b‾−g‾(a‾))δ(a‾−a^‾)da‾=δ(b‾−g(a^‾)⏟b^‾) \begin{aligned} f(\underline{b}) &= \int_{\mathbb{R}^A} \delta(\underline{b} - \underline{g}(\underline{a})) f(\underline{a}) d\underline{a} \\\\ &= \int_{\mathbb{R}^A} \delta(\underline{b} - \underline{g}(\underline{a})) \delta(\underline{a} - \underline{\hat{a}}) d\underline{a} \\\\ &= \delta(\underbrace{\underline{b} - g(\underline{\hat{a}})}_{\underline{\hat{b}}}) \end{aligned}

Das erwartete Ergebnis ist dann

f(b‾)=δ(b‾−b^‾) f(\underline{b}) = \delta(\underline{b} - \underline{\hat{b}})

mit b^‾=g‾(a^‾)\underline{\hat{b}} = \underline{g}(\underline{\hat{a}}).

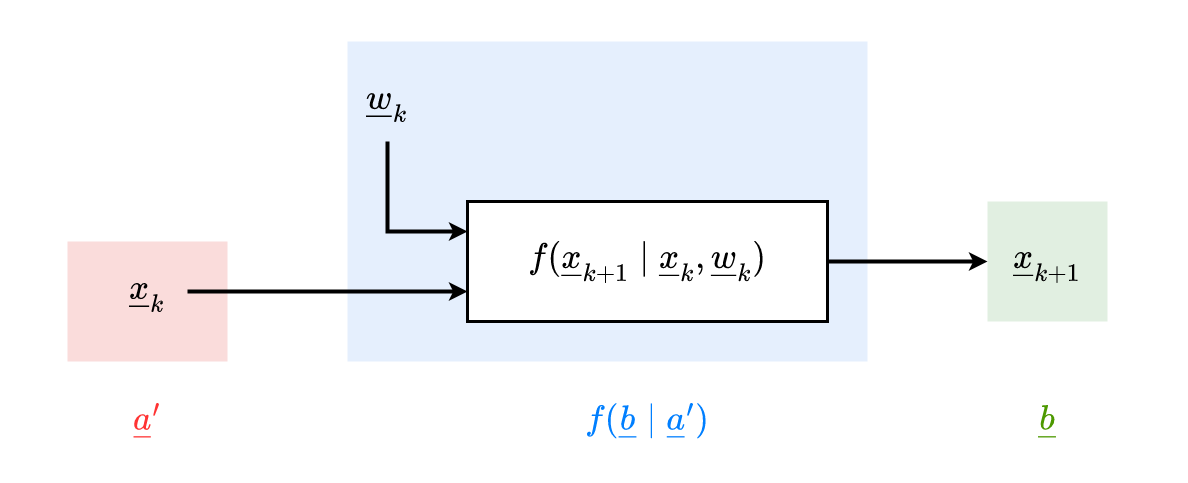
Probabilistisches nichtlineares Systemmodell

Allgemeines Systemmodell

x‾k+1=a‾k(x‾k,w‾k) \underline{x}_{k+1} = \underline{a}_k(\underline{x}_k, \underline{w}_k)

in Form f(b‾∣a‾)f(\underline{b} \mid \underline{a}) bringen:

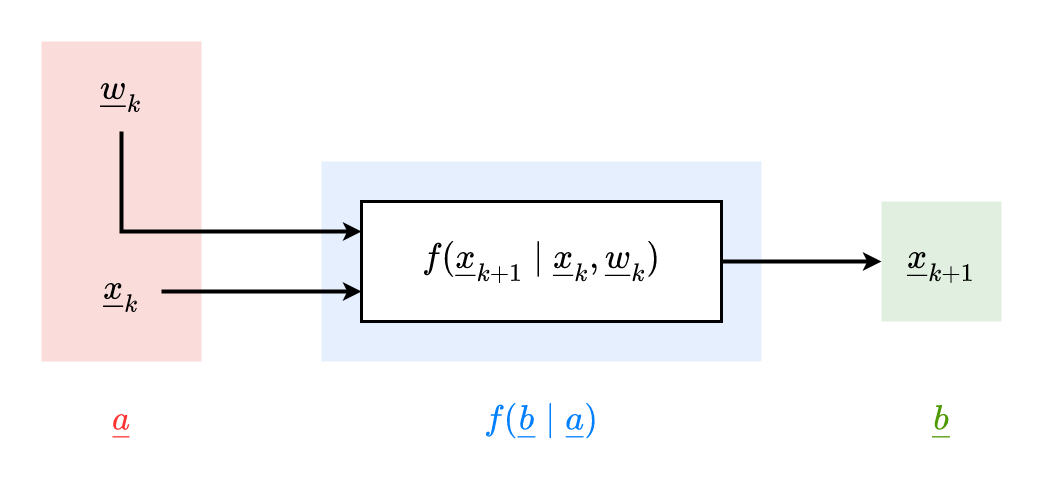allg_sys-prob_nichtlin_sys.drawio a‾=[x‾kw‾k],b‾=x‾k+1 \underline{a}=\left[\begin{array}{c} \underline{x}_{k} \\ \underline{w}_{k} \end{array}\right], \quad \underline{b}=\underline{x}_{k+1} f(b‾∣a‾)=δ(x‾k+1−a‾k(x‾k,w‾k)) f(\underline{b} \mid \underline{a}) = \delta \left(\underline{x}_{k+1} - \underline{a}_k(\underline{x}_k, \underline{w}_k)\right)

Mit anderen Systemgrenzen:

allg_sys-Copy of prob_nichtlin_sys.drawio

f(b‾∣a‾′)=f(x‾k+1∣x‾k)=∫RNf(x‾k+1∣x‾k,w‾k)⏟f(b‾∣a‾)⋅f(w‾k)dw‾k \begin{aligned} f(\underline{b} \mid \underline{a}^\prime) &= f(\underline{x}_{k+1} \mid \underline{x}_k) \\\\ &= \int_{\mathbb{R}^N} \underbrace{f(\underline{x}_{k+1} \mid \underline{x}_k, \underline{w}_k)}_{f(\underline{b} \mid \underline{a})} \cdot f(\underline{w}_k) d\underline{w}_k \end{aligned}

In diesem Fall enthält f(b‾∣a‾)f(\underline{b} \mid \underline{a}) Systemrauschen →\rightarrow ist nicht mehr durch δ\delta-funktion beschreibbar.