Docs
Notes
SI
Allgemeine Systeme
Dirac’sche Deltafunktion

Dirac’sche Deltafunktion

Mehr zu Dirac’sche Deltafunktion siehe:

Eigenschaften

Symmetrie

δ(x)=δ(−x) \delta (x) = \delta (-x)

Skalierung

δ(ax)=1∣a∣δ(x) \delta (ax) = \frac{1}{|a|}\delta (x)

Kompizierte Argumente

δ(g(x))=∑i=1N1∣g′(xi)∣δ(x−xi) \delta (g(x)) = \sum_{i=1}^N \frac{1}{|g^\prime(x_i)|}\delta (x - x_i)

wobei

  • g(xi)=0g(x_i) = 0 (also xix_i sind Nullstellen, i=1,2,…,Ni = 1, 2, \dots, N)
  • g′(xi)≠0g^\prime(x_i) \neq 0

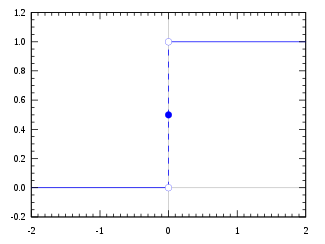
Ableitung der Heaviside Step Funktion

δ(x)=ddxH(x) \delta(x) = \frac{d}{dx} H(x)

wobei H(x)H(x) ist die Heaviside Step Funktion

H(x):={1,x>00,x≤0 H(x):= \begin{cases}1, & x>0 \\ 0, & x \leq 0\end{cases}

Dirac distribution CDF.svg