Docs
Notes
SI
Allgemeine Systeme
Faktorgraphen und Message Passing

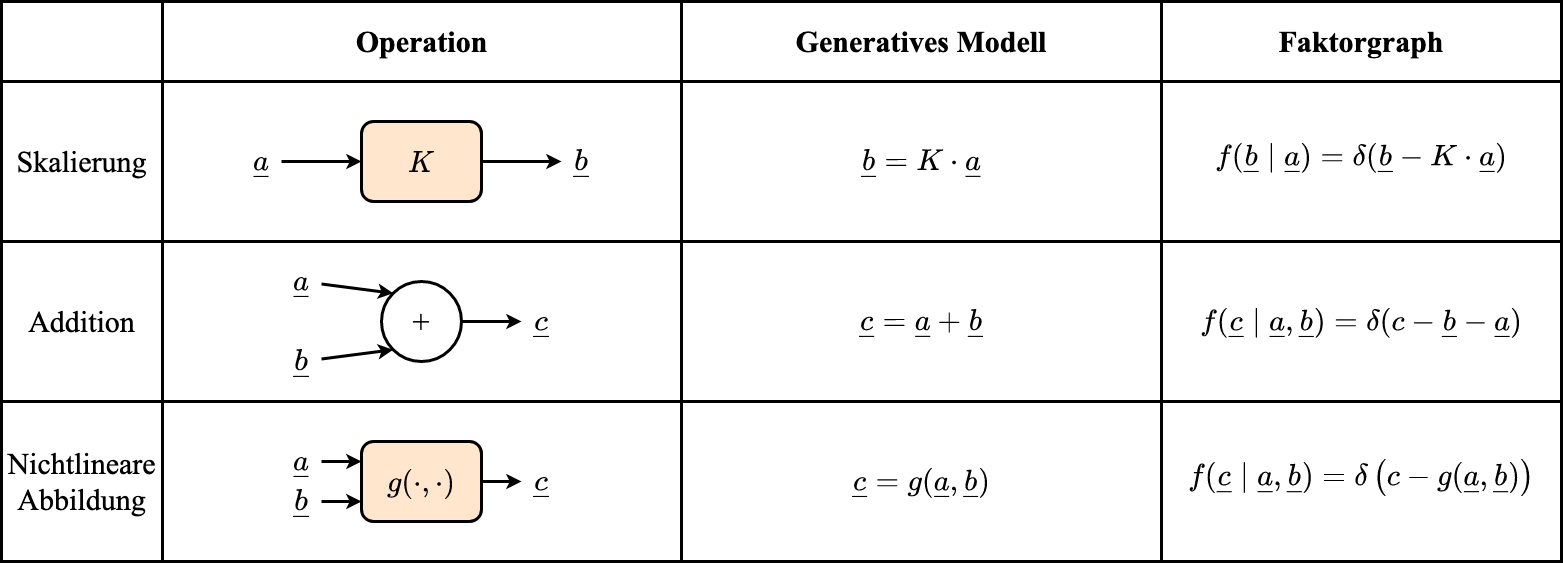
Faktorgraphen und Message Passing

Faktorgraphen

Regeln

allg_sys-Faktorgraph.drawio (1)

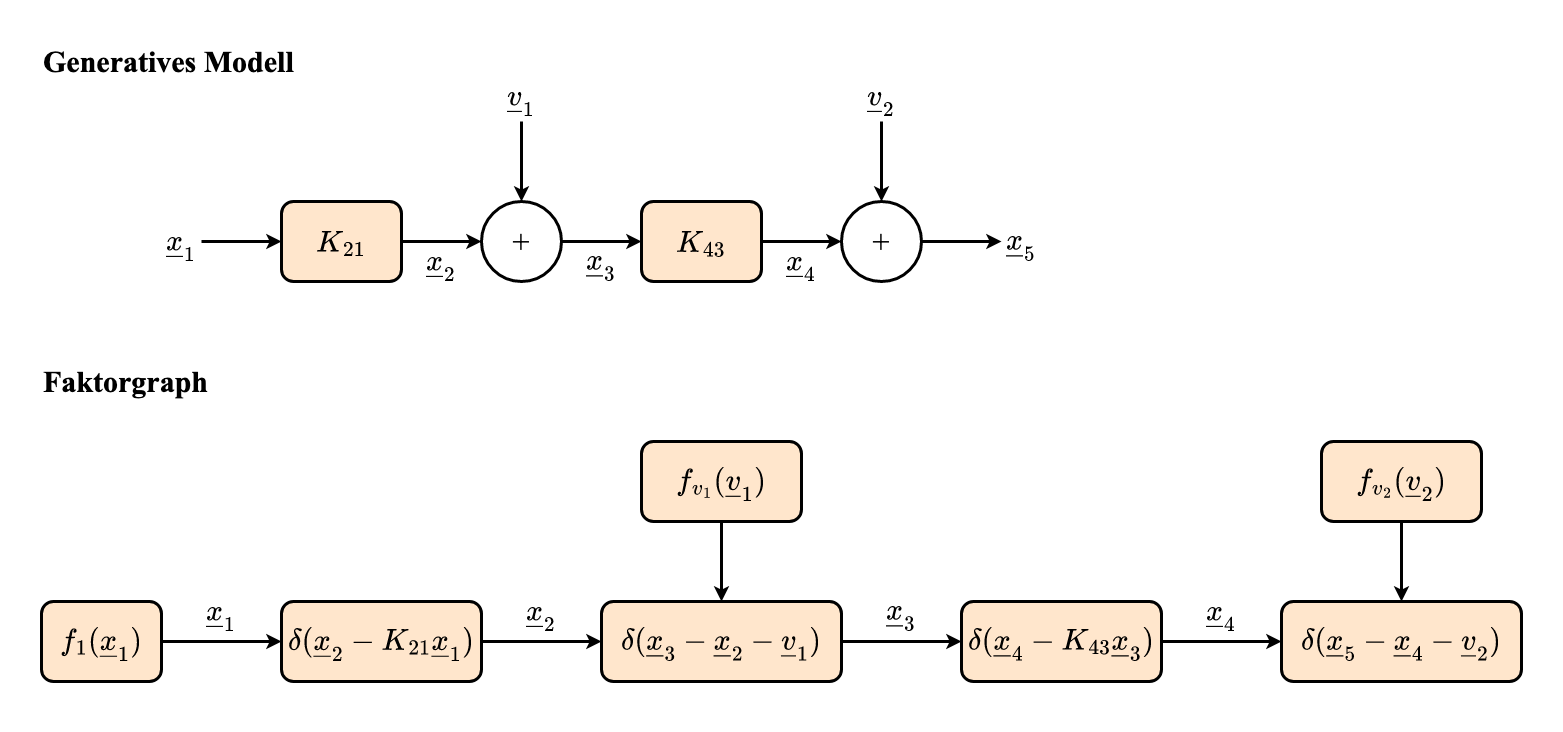
Beispiel

allg_sys-Faktorgraph_Bsp.drawio

Message Passing

Definiere Nachricht an einer Kante

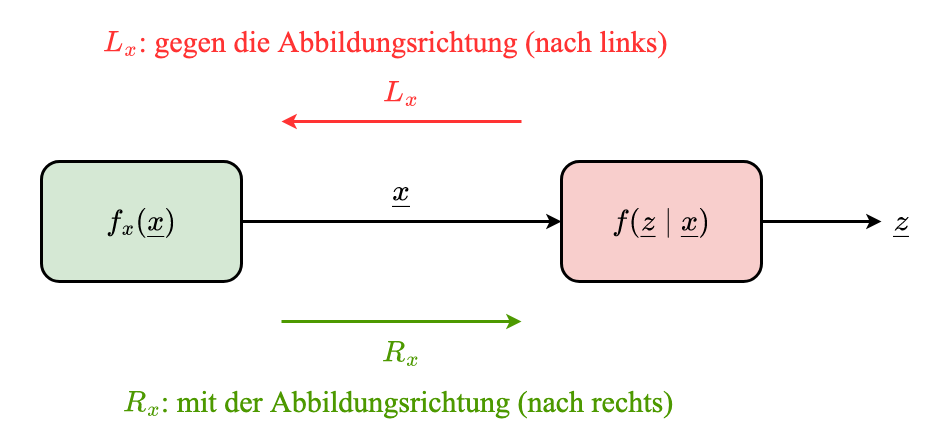
allg_sys-Nachricht.drawio (1)

Schnitt zur Aufteilung eines Systems in 2 Teile

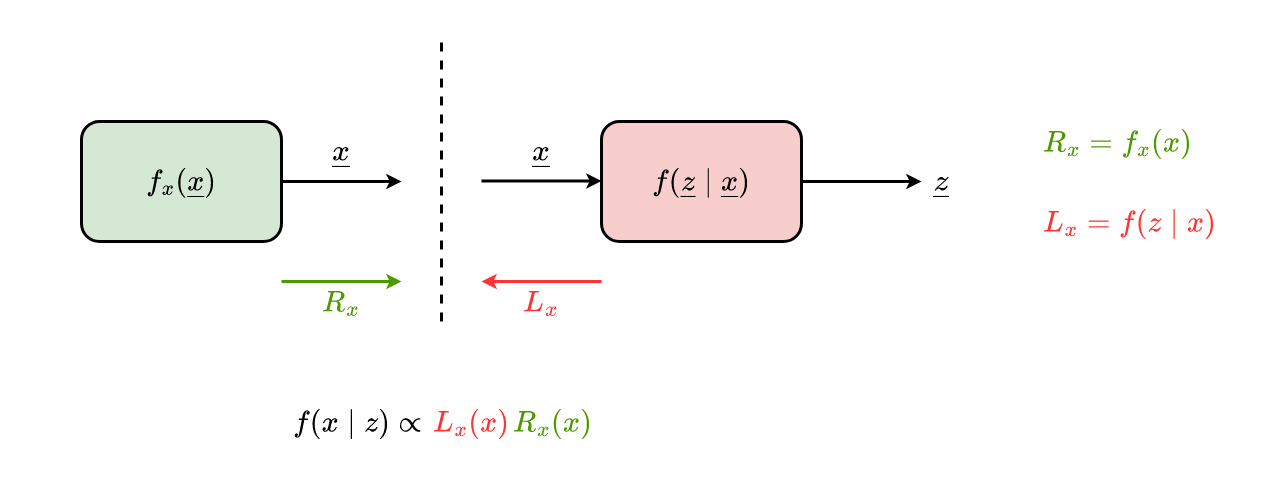
allg_sys-System_Schnitt.drawio (1)

Betrachtung von Block mit einem Eingang und einem Ausgang

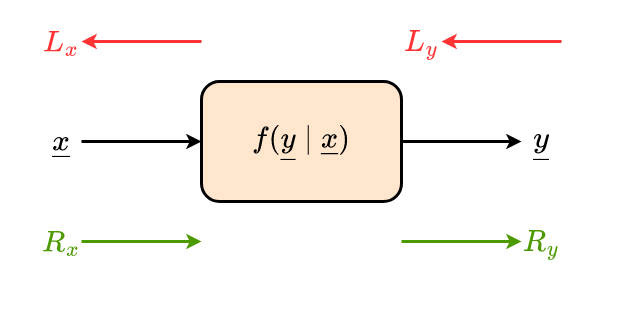
allg_sys-Block.drawio (2)

Gegeben: $R_x$ und $L_y$

$$ \begin{aligned} &R_{y}(y)=\int f(y \mid x) \cdot R_{x}(x) d x \\ &L_{x}(x)=\int f(y \mid x) \cdot L_{y}(y) d y \end{aligned} $$

Speizialfall: Lineares System

$$ \begin{aligned} y &= Hx\\ \Rightarrow f(y \mid x) &= \delta(y - Hx) \end{aligned} $$ $$ \begin{aligned} R_y(y) &= \int \delta(y-Hx) R_x(x) dx \quad \mid g(x):=y-Hx, g^\prime(x) = -H, x_1 = \frac{y}{H}\\ &= \int \frac{1}{|H|} \delta(x - \frac{y}{H}) R_x(x) dx \\ &= \frac{1}{|H|} R_x(\frac{y}{H}) \end{aligned} $$ $$ \begin{aligned} L_{x}(x) &=\int f(y \mid x) L_{y}(y) d y \\ &=\int \delta(y-H x) \cdot L_{y}(y) d y \\ &=L_{y}(H \cdot x) \end{aligned} $$

Beispiel

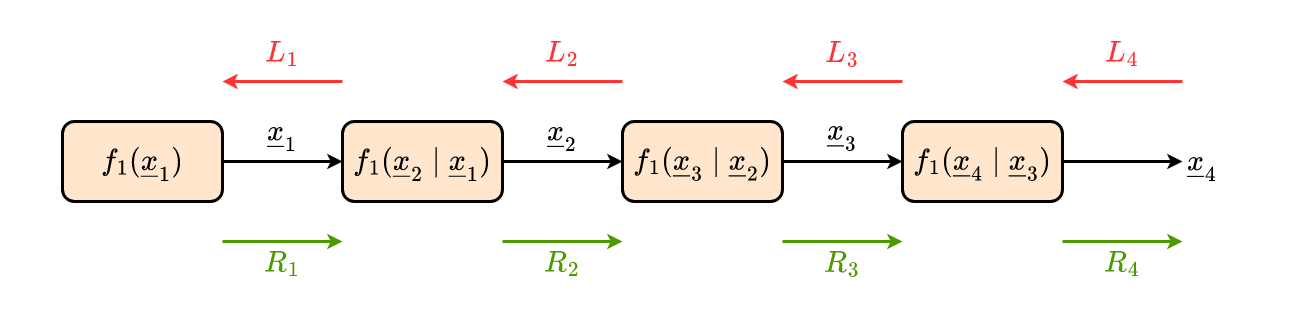
allg_sys-Message_Passing_Bsp.drawio

  • Gegeben: $\underline{\hat{x}}_4$

  • Gesucht: $f(\underline{x}_2 \mid \underline{\hat{x}}_4)$

  • Ziel: Rekursive Berechnung der Nachrichten

  • Direkt gegeben:

    $$ R_{1}\left(\underline{x}_{1}\right)=f_{1}\left(\underline{x}_{1}\right) \quad L_{3}\left(\underline{x}_{3}\right)=f\left(\underline{\hat{x}}_{4} \mid \underline{x}_{3}\right) $$

  • Benötigt: $L_2(\underline{x}_2)$ und $R_2(\underline{x}_2)$

    $$ \begin{aligned} &R_{2}\left(\underline{x}_{2}\right)=\int f\left(\underline{x}_{2} \mid \underline{x}_{1}\right) R_{1}\left(\underline{x}_{1}\right) d \underline{x}_{1} \\ &L_{2}\left(\underline{x}_{2}\right)=\int f\left(\underline{x}_{3} \mid \underline{x}_{2}\right) L_{3}\left(\underline{x}_{3}\right) d \underline{x}_{3} \end{aligned} $$

$\Rightarrow$ Fusionsergebnis:

$$ f\left(\underline{x}_{2} \mid \underline{\hat{x}}_{4}\right) \propto L_{2}\left(\underline{x}_{2}\right) \cdot R_{2}\left(\underline{x}_{2}\right) $$