Zusammenfassung

Vorwärtsinferenz

• Gegeben
  • $f_a(a)$
  • $g(a)$
• Gesucht: $f_b(b)$

Schritte:

1. Umforme $f(b \mid a) = \delta(b - g(a))$ mit

   $$ \delta (g(x)) = \sum_{i=1}^N \frac{1}{|g^\prime(x_i)|}\delta (x - x_i) $$

   wobei

   • $g(x_i) = 0$ (also $x_i$ sind Nullstellen, $i = 1, 2, \dots, N$)
   • $g^\prime(x_i) \neq 0$

2. Berechne $f_b(b)$ mithilfe von Chapman-Kolmogorov-Gleichung

   $$ f(b) = \int f(b \mid a) f(a) da $$

   und setze die Unformung von $f(b \mid a)$ von Schritt 1 ein. Dann kriege die gesuchte Dichtefunktion $f_b(b)$ in Abhängigkeit von $f_a(a)$.

Rückwartsinferenz

Konkrete Messung

1. Umforme $f_b(b \mid a) = \delta(b - g(a))$ mit

   $$ \delta (g(x)) = \sum_{i=1}^N \frac{1}{|g^\prime(x_i)|}\delta (x - x_i) $$

   wobei

   • $g(x_i) = 0$ (also $x_i$ sind Nullstellen, $i = 1, 2, \dots, N$)
   • $g^\prime(x_i) \neq 0$

2. Berechne $f_b(b)$

   $$ f_b(b) = \int f_{a, b}(a, b) da = \int f_{b}(b \mid a) f_a(a) da $$

   mit Einsetzen der Unformung von $f(b \mid a)$ von Schritt 1 ein

3. Berechne $f_a(a \mid b)$ mithilfe von Bayes Regeln

   $$ f_a(a \mid b) = \frac{f_a(b \mid a) f_a(a)}{f_b(b)} = \frac{\overbrace{\delta(b - g(a))}^{\text{Schritt 1}} f_a(a)}{\underbrace{f_b(b)}_{\text{Schritt 2}}} $$

Unsichere Messung

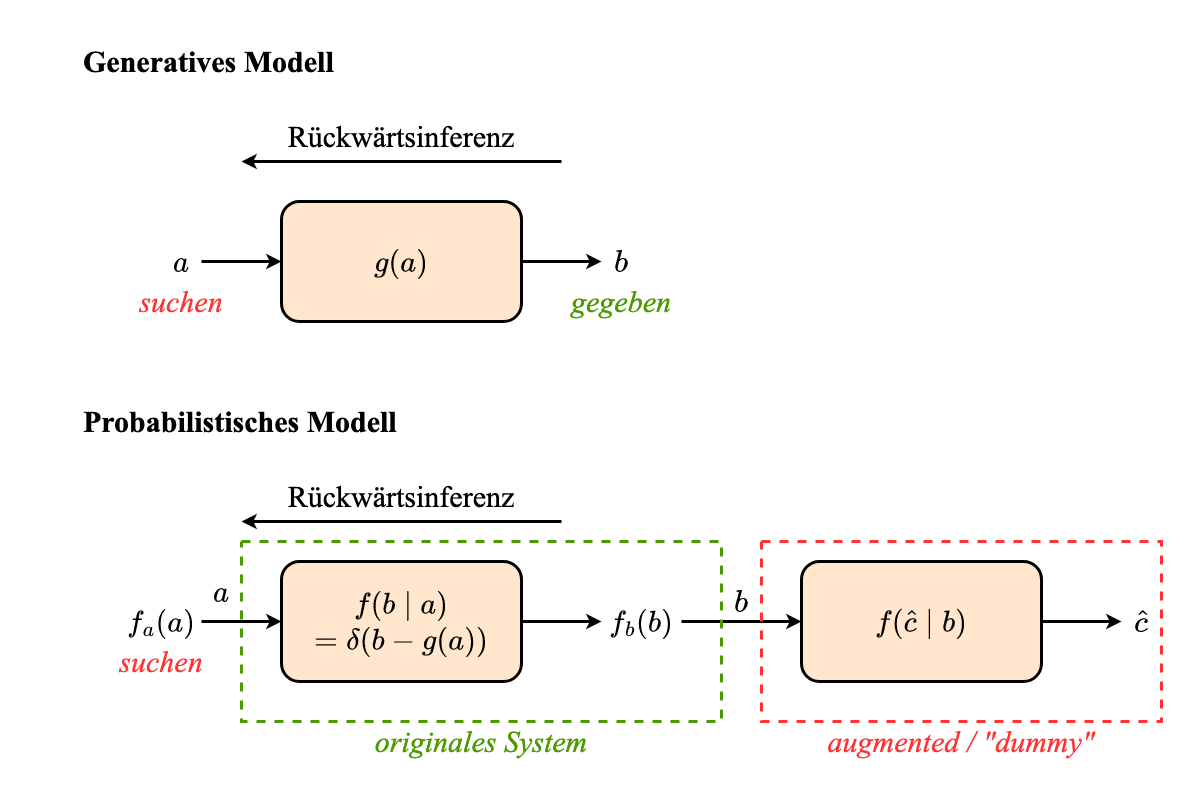
Schritte:

0. Erweitere das System um eine zusätzliche stochastische Abbildung und einen festen Ausgang $\hat{z}$

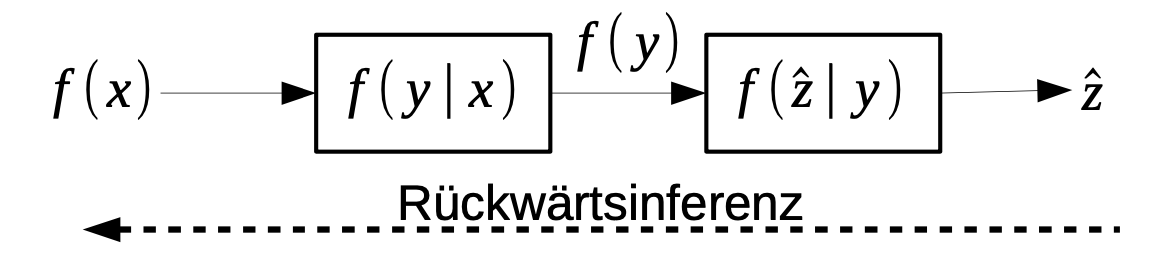
1. Bestimme $f(\hat{z} \mid y)$

   $$ \begin{aligned} f(\hat{z} \mid y) &= \frac{f(y \mid \hat{z})f(\hat{z})}{f(y)} \\\\ &= \frac{f(y \mid \hat{z})f(\hat{z})}{\int f(y, x) dx} \\\\ &= \frac{f(y \mid \hat{z})f(\hat{z})}{\int f(y|x)f(x) dx} \\\\ &= \frac{f(y \mid \hat{z})f(\hat{z})}{\int \delta(y - g(x)) f(x) dx} \\\\ \end{aligned} $$

   Und setze die Umformung von $\delta(y - g(x))$

   $$ \delta (g(x)) = \sum_{i=1}^N \frac{1}{|g^\prime(x_i)|}\delta (x - x_i) $$
   • $g(x_i) = 0$ (also $x_i$ sind Nullstellen, $i = 1, 2, \dots, N$)
   • $g^\prime(x_i) \neq 0$

   ein.

2. Berechung der Rückwärtsinferenz $f(x \mid \hat{z})$

   $$ \begin{aligned} f(x \mid \hat{z}) &=\frac{1}{f\left(\hat{z}\right)} \cdot f(x, z) \quad \mid \text{Marginalisierung nach } y\\ &=\frac{1}{f(\hat{z})} \int f(x, y, z) d y \\ &=\frac{1}{f(\hat{z})} \int f(\hat{z} \mid y, x) \cdot f(y , x) d y \quad \mid \hat{z}, x \text{ sind unabhängig}\\ &=\frac{1}{f(\hat{z})} \int f(\hat{z} \mid y) \cdot f(y \mid x) \cdot f(x) d y \\ &=\frac{1}{f(\hat{z})} \int \underbrace{f(\hat{z} \mid y)}_{\text{Berechnet in Schritt 1}} \cdot \underbrace{f(y \mid x)}_{\text{Systemmodell}} \cdot f(x) d y \end{aligned} $$