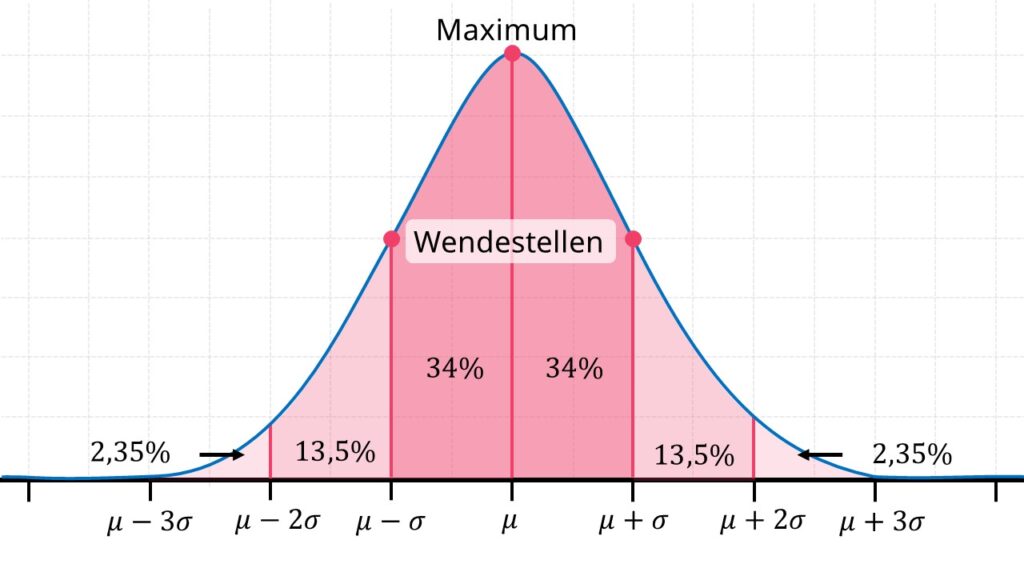
GauΓverteilung Skalarer Fall (1D) f ( x ) = 1 2 Ο Ο exp β‘ { β 1 2 ( x β x ^ ) 2 Ο 2 }
f(x)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left\{-\frac{1}{2} \frac{(x-\hat{x})^{2}}{\sigma^{2}}\right\}
f ( x ) = 2 Ο β Ο 1 β exp { β 2 1 β Ο 2 ( x β x ^ ) 2 β } Erwartungswert
E f { x } = x ^
E_{f}\{x\}=\hat{x}
E f β { x } = x ^ Varianz
E f { ( x β x ^ ) 2 } = Ο 2
E_{f}\left\{(x-\hat{x})^{2}\right\}=\sigma^{2}
E f β { ( x β x ^ ) 2 } = Ο 2 Given the parameters ΞΌ \mu ΞΌ Ο \sigma Ο f ~ x \tilde{f}_x f ~ β x β f ~ x \tilde{f}_x f ~ β x β
2D Normalverteilung f x y ( x , y ) = 1 2 Ο Ο x Ο y 1 β r 2 exp β‘ { β 1 2 Q ( x , y ) } Q ( x , y ) = 1 1 β r { ( x β x ^ ) 2 Ο x 2 β 2 r x β x ^ Ο x y β y ^ Ο y + ( y β y ^ ) 2 Ο y 2 }
\begin{aligned}
f_{x y}(x, y)&=\frac{1}{2 \pi \sigma_{x} \sigma_{y} \sqrt{1-r^{2}}} \exp \left\{-\frac{1}{2} Q(x, y)\right\} \\
Q(x, y)&=\frac{1}{1-r}\left\{\frac{(x-\hat{x})^{2}}{\sigma_{x}^{2}}-2 r \frac{x-\hat{x}}{\sigma_{x}} \frac{y-\hat{y}}{\sigma_{y}}+\frac{(y-\hat{y})^{2}}{\sigma_{y}^{2}}\right\}
\end{aligned}
f x y β ( x , y ) Q ( x , y ) β = 2 Ο Ο x β Ο y β 1 β r 2 β 1 β exp { β 2 1 β Q ( x , y ) } = 1 β r 1 β { Ο x 2 β ( x β x ^ ) 2 β β 2 r Ο x β x β x ^ β Ο y β y β y ^ β β + Ο y 2 β ( y β y ^ β ) 2 β } β r β [ β 1 , 1 ] r \in [-1, 1] r β [ β 1 , 1 ] Ο \rho Ο Alternativ
f x y ( x , y ) = N ( [ x y ] , [ x ^ y ^ ] , [ C x x C x y C y x C y y ] )
f_{x y}(x, y)=\mathcal{N} \left(\left[\begin{array}{l}
x \\
y
\end{array}\right],\left[\begin{array}{l}
\hat{x} \\
\hat{y}
\end{array}\right],\left[\begin{array}{ll}
C_{x x} & C_{x y} \\
C_{y x} & C_{y y}
\end{array}\right]\right)
f x y β ( x , y ) = N ( [ x y β ] , [ x ^ y ^ β β ] , [ C xx β C y x β β C x y β C yy β β ] ) mit
[ c x x c x y c y x c y y ] = [ Ο x 2 r Ο x Ο y r Ο x Ο y Ο y 2 ]
\left[\begin{array}{ll}
c_{x x} & c_{x y} \\
c_{y x} & c_{y y}
\end{array}\right]=\left[\begin{array}{lc}
\sigma_{x}^{2} & r \sigma_{x} \sigma_{y} \\
r \sigma_{x} \sigma_{y} & \sigma_{y}^{2}
\end{array}\right]
[ c xx β c y x β β c x y β c yy β β ] = [ Ο x 2 β r Ο x β Ο y β β r Ο x β Ο y β Ο y 2 β β ] Correlationskoeffizient Correlation of bivariate Gaussian distribution (Ο \rho Ο
unkorreliert (r = 0 r = 0 r = 0
β x , y \Rightarrow \boldsymbol{x}, \boldsymbol{y} β x , y β \Rightarrow β x , y \boldsymbol{x}, \boldsymbol{y} x , y f x , y = f x ( x ) f y ( y ) f_{\boldsymbol{x}, \boldsymbol{y}} = f_{\boldsymbol{x}}(x) f_{\boldsymbol{y}}(y) f x , y β = f x β ( x ) f y β ( y ) positiv korreliert (r > 0 r > 0 r > 0
positiv korreliert (r < 0 r < 0 r < 0
N N N f x ( x ) = 1 ( 2 Ο ) N β
β£ C β£ exp β‘ { β 1 2 ( x βΎ β x ^ βΎ ) β€ C β 1 ( x βΎ β x ^ βΎ ) }
f_{\boldsymbol{x}}(x)=\frac{1}{\sqrt{(2 \pi)^{N} \cdot|\mathbf{C}|}} \exp \left\{-\frac{1}{2}(\underline{x}-\underline{\hat{x}})^{\top} \mathbf{C}^{-1}(\underline{x}-\underline{\hat{x}})\right\}
f x β ( x ) = ( 2 Ο ) N β
β£ C β£ β 1 β exp { β 2 1 β ( x β β x ^ β ) β€ C β 1 ( x β β x ^ β ) } x ^ βΎ \underline{\hat{x}} x ^ β C \mathbf{C} C 
