Extended Kalman Filter Motivation Linear systems do not exist in reality. We have to deal with nonlinear discrete-time systems
x k β current state = f k β 1 ( x k β 1 β previous state , u k β 1 β inputs , w k β 1 β process noise ) y k β measurement = h k ( x k , v k β measurement noise )
\begin{aligned}
\underbrace{\mathbf{x}_{k}}_{\text{current state}}&=\mathbf{f}_{k-1}(\underbrace{\mathbf{x}_{k-1}}_{\text{previous state}}, \underbrace{\mathbf{u}_{k-1}}_{\text{inputs}}, \underbrace{\mathbf{w}_{k-1}}_{\text{process noise}}) \\\\
\underbrace{\mathbf{y}_{k}}_{\text{measurement}}&=\mathbf{h}_{k}(\mathbf{x}_{k}, \underbrace{\mathbf{v}_{k}}_{\text{measurement noise}})
\end{aligned}
current state x k β β β measurement y k β β β β = f k β 1 β ( previous state x k β 1 β β β , inputs u k β 1 β β β , process noise w k β 1 β β β ) = h k β ( x k β , measurement noise v k β β β ) β How can we adapt Kalman Filter to nonlinear discrete-time systems?
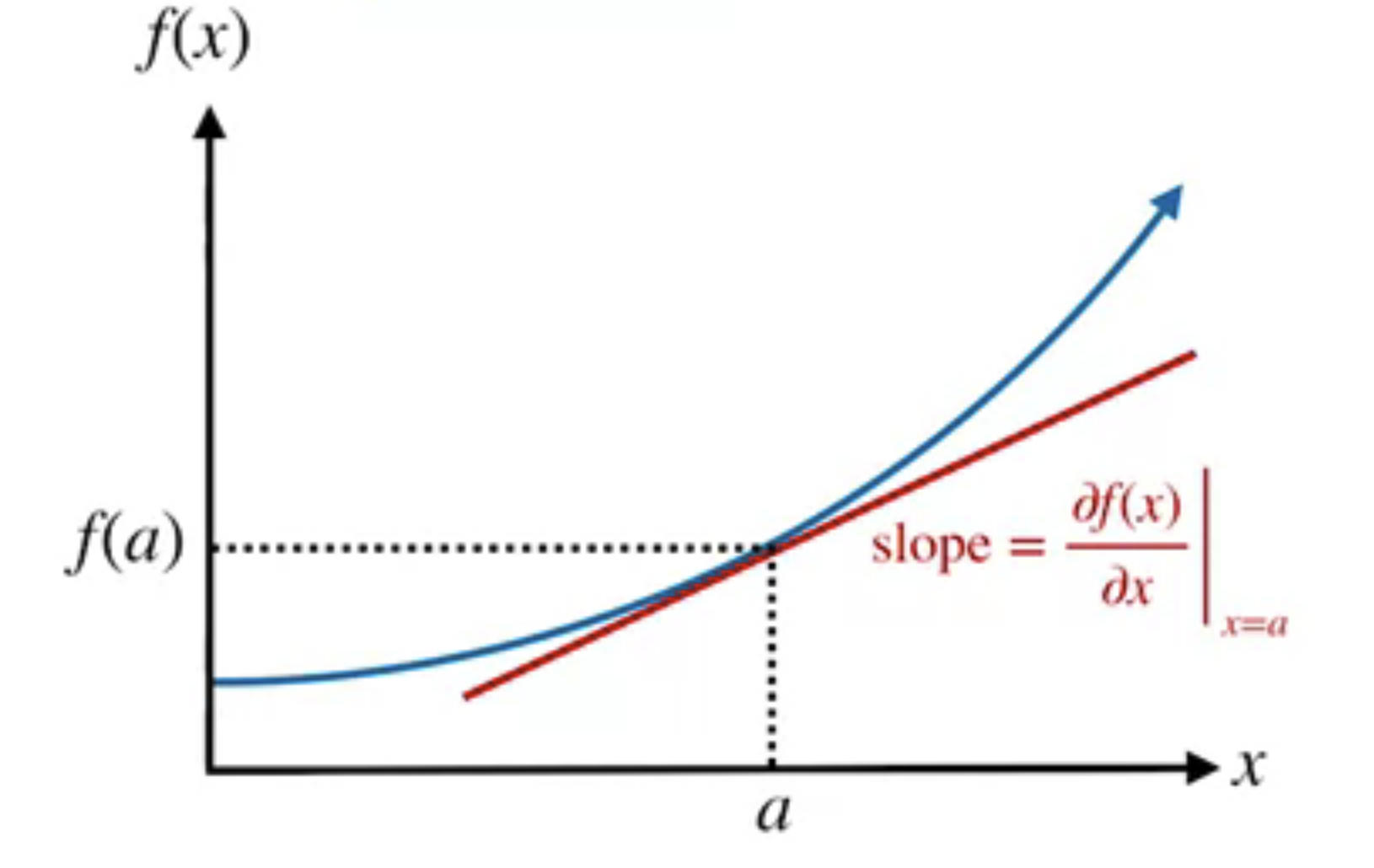
π‘ Idea: Linearizing a Nonlinear System Choose an operating point a a a
We compute this linear approximation using a first-order Taylor expansion
f ( x ) β f ( a ) + β f ( x ) β x β£ x = a ( x β a )
f(x) \approx f(a)+\left.\frac{\partial f(x)}{\partial x}\right|_{x=a}(x-a)
f ( x ) β f ( a ) + β x β f ( x ) β β x = a β ( x β a ) Extended Kalman Filter For EKF, we choose the operationg point to be our most recent state estimate, our known input, and zero noise.
F k β 1 , L k β 1 , H k , M k \mathbf{F}_{k-1}, \mathbf{L}_{k-1}, \mathbf{H}_{k}, \mathbf{M}_{k} F k β 1 β , L k β 1 β , H k β , M k β
Intuitively, the Jacobian matrix tells you how fast each output of the function is changing along each input dimension.
With our linearized models and Jacobians, we can now use the Kalman Filter equations.
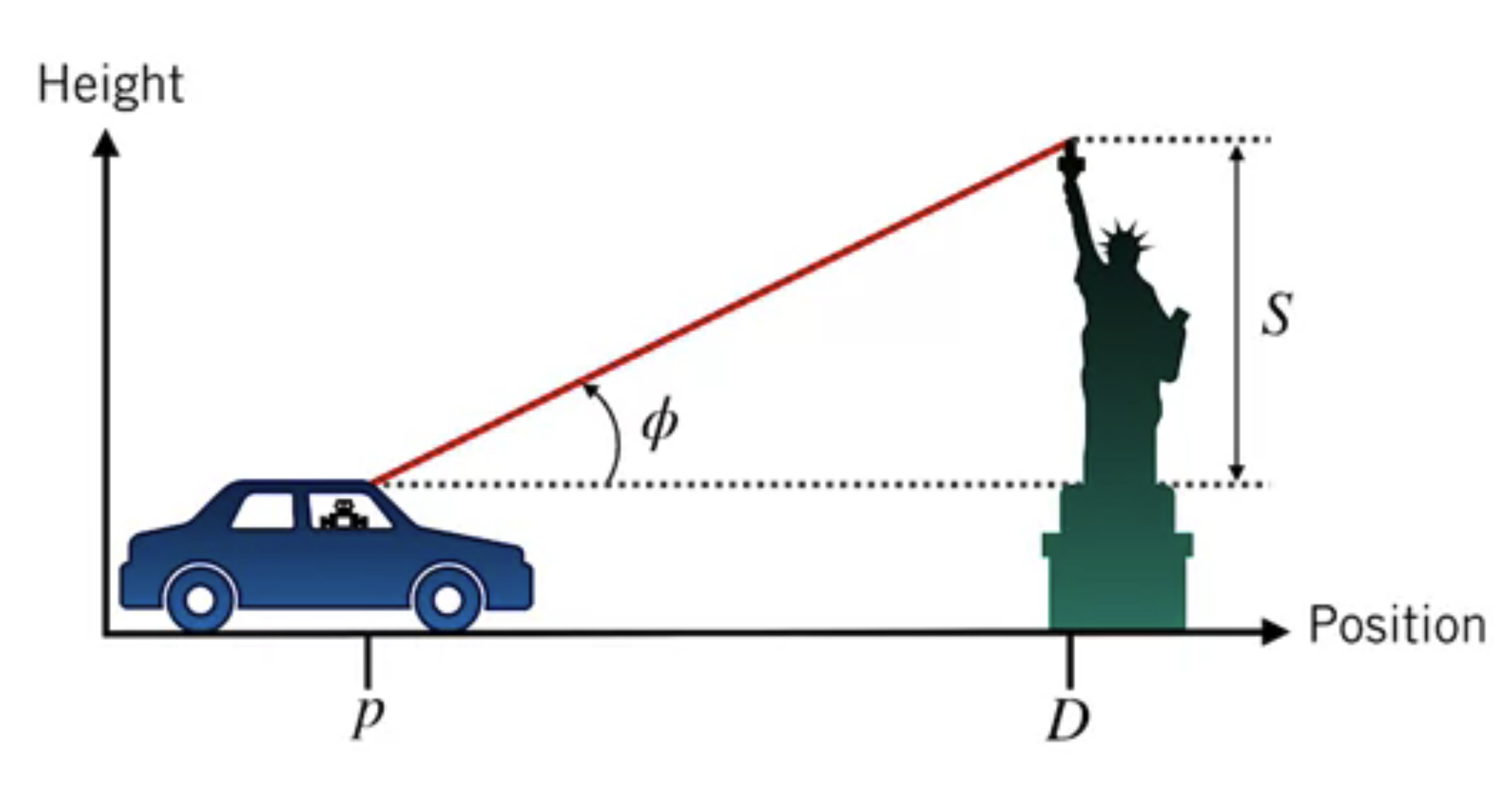
We still use the nonlinear model to propagate the mean of the state estimate in prediction step and compute the measurement residual innovation in correction step. Example Similar to the self-driving car localisation example in Linear Kalman Fitler, but this time we use an onboard sensor, a camera, to measure the altitude of distant landmarks relative to the horizon.
(S S S D D D
Sate:
x = [ p p Λ ]
\mathbf{x}=\left[\begin{array}{l}
p \\
\dot{p}
\end{array}\right]
x = [ p p Λ β β ] Input:
u = p Β¨
\mathbf{u}=\ddot{p}
u = p Β¨ β Motion/Process model
x k = f ( x k β 1 , u k β 1 , w k β 1 ) = [ 1 Ξ t 0 1 ] x k β 1 + [ 0 Ξ t ] u k β 1 + w k β 1
\begin{aligned}
\mathbf{x}_{k} &=\mathbf{f}\left(\mathbf{x}_{k-1}, \mathbf{u}_{k-1}, \mathbf{w}_{k-1}\right) \\\\
&=\left[\begin{array}{cc}
1 & \Delta t \\
0 & 1
\end{array}\right] \mathbf{x}_{k-1}+\left[\begin{array}{c}
0 \\
\Delta t
\end{array}\right] \mathbf{u}_{k-1}+\mathbf{w}_{k-1}
\end{aligned}
x k β β = f ( x k β 1 β , u k β 1 β , w k β 1 β ) = [ 1 0 β Ξ t 1 β ] x k β 1 β + [ 0 Ξ t β ] u k β 1 β + w k β 1 β β Landmark measurement model (nonlinear!)
y k = Ο k = h ( p k , v k ) = tan β‘ β 1 ( S D β p k ) + v k
\begin{aligned}
y_{k} &=\phi_{k}=h\left(p_{k}, v_{k}\right) \\\\
&=\tan ^{-1}\left(\frac{S}{D-p_{k}}\right)+v_{k}
\end{aligned}
y k β β = Ο k β = h ( p k β , v k β ) = tan β 1 ( D β p k β S β ) + v k β β Noise densities
v k βΌ N ( 0 , 0.01 ) w k βΌ N ( 0 , ( 0.1 ) 1 2 Γ 2 )
v_{k} \sim \mathcal{N}(0,0.01) \quad \mathbf{w}_{k} \sim \mathcal{N}\left(\mathbf{0},(0.1) \mathbf{1}_{2 \times 2}\right)
v k β βΌ N ( 0 , 0.01 ) w k β βΌ N ( 0 , ( 0.1 ) 1 2 Γ 2 β ) The Jacobian matrices in this example are:
Given
x ^ 0 βΌ N ( [ 0 5 ] , [ 0.01 0 0 1 ] ) Ξ t = 0.5 s u 0 = β 2 [ m / s 2 ] y 1 = Ο / 6 [ r a d ] S = 20 [ m ] D = 40 [ m ]
\begin{array}{l}
\hat{\mathbf{x}}_{0} \sim \mathcal{N}\left(\left[\begin{array}{l}
0 \\
5
\end{array}\right], \quad\left[\begin{array}{cc}
0.01 & 0 \\
0 & 1
\end{array}\right]\right)\\
\Delta t=0.5 \mathrm{~s}\\
u_{0}=-2\left[\mathrm{~m} / \mathrm{s}^{2}\right] \quad y_{1}=\pi / 6[\mathrm{rad}]\\
S=20[m] \quad D=40[m]
\end{array}
x ^ 0 β βΌ N ( [ 0 5 β ] , [ 0.01 0 β 0 1 β ] ) Ξ t = 0.5 s u 0 β = β 2 [ m / s 2 ] y 1 β = Ο /6 [ rad ] S = 20 [ m ] D = 40 [ m ] β What is the position estimate p ^ 1 \hat{p}_1 p ^ β 1 β
Prediction:
x Λ 1 = f 0 ( x ^ 0 , u 0 , 0 ) [ p Λ 1 p Λ 1 ] = [ 1 0.5 0 1 ] [ 0 5 ] + [ 0 0.5 ] ( β 2 ) = [ 2.5 4 ] P Λ 1 = F 0 P ^ 0 F 0 T + L 0 Q 0 L 0 T P Λ 1 = [ 1 0.5 0 1 ] [ 0.01 0 0 1 ] [ 1 0 0.5 1 ] + [ 1 0 0 1 ] [ 0.1 0 0 0.1 ] [ 1 0 0 1 ] = [ 0.36 0.5 0.5 1.1 ]
\begin{array}{c}
\check{\mathbf{x}}_{1}=\mathbf{f}_{0}\left(\hat{\mathbf{x}}_{0}, \mathbf{u}_{0}, \mathbf{0}\right) \\
{\left[\begin{array}{c}
\check{p}_{1} \\
\dot{p}_{1}
\end{array}\right]=\left[\begin{array}{cc}
1 & 0.5 \\
0 & 1
\end{array}\right]\left[\begin{array}{l}
0 \\
5
\end{array}\right]+\left[\begin{array}{c}
0 \\
0.5
\end{array}\right](-2)=\left[\begin{array}{c}
2.5 \\
4
\end{array}\right]} \\\\
\check{\mathbf{P}}_{1}=\mathbf{F}_{0} \hat{\mathbf{P}}_{0} \mathbf{F}_{0}^{T}+\mathbf{L}_{0} \mathbf{Q}_{0} \mathbf{L}_{0}^{T} \\
\check{\mathbf{P}}_{1}=\left[\begin{array}{cc}
1 & 0.5 \\
0 & 1
\end{array}\right]\left[\begin{array}{cc}
0.01 & 0 \\
0 & 1
\end{array}\right]\left[\begin{array}{cc}
1 & 0 \\
0.5 & 1
\end{array}\right]+\left[\begin{array}{cc}
1 & 0 \\
0 & 1
\end{array}\right]\left[\begin{array}{cc}
0.1 & 0 \\
0 & 0.1
\end{array}\right]\left[\begin{array}{cc}
1 & 0 \\
0 & 1
\end{array}\right]=\left[\begin{array}{cc}
0.36 & 0.5 \\
0.5 & 1.1
\end{array}\right]
\end{array}
x Λ 1 β = f 0 β ( x ^ 0 β , u 0 β , 0 ) [ p Λ β 1 β p Λ β 1 β β ] = [ 1 0 β 0.5 1 β ] [ 0 5 β ] + [ 0 0.5 β ] ( β 2 ) = [ 2.5 4 β ] P Λ 1 β = F 0 β P ^ 0 β F 0 T β + L 0 β Q 0 β L 0 T β P Λ 1 β = [ 1 0 β 0.5 1 β ] [ 0.01 0 β 0 1 β ] [ 1 0.5 β 0 1 β ] + [ 1 0 β 0 1 β ] [ 0.1 0 β 0 0.1 β ] [ 1 0 β 0 1 β ] = [ 0.36 0.5 β 0.5 1.1 β ] β Correction:
K 1 = P Λ 1 H 1 T ( H 1 P Λ 1 H 1 T + M 1 R 1 M 1 T ) β 1 = [ 0.36 0.5 0.5 1.1 ] [ 0.011 0 ] ( [ 0.011 0 ] [ 0.36 0.5 0.5 1.1 ] [ 0.011 0 ] + 1 ( 0.01 ) ( 1 ) ) β 1 = [ 0.40 0.55 ]
\begin{aligned}
\mathbf{K}_{1} &=\check{\mathbf{P}}_{1} \mathbf{H}_{1}^{T}\left(\mathbf{H}_{1} \check{\mathbf{P}}_{1} \mathbf{H}_{1}^{T}+\mathbf{M}_{1} \mathbf{R}_{1} \mathbf{M}_{1}^{T}\right)^{-1} \\
&=\left[\begin{array}{cc}
0.36 & 0.5 \\
0.5 & 1.1
\end{array}\right]\left[\begin{array}{c}
0.011 \\
0
\end{array}\right]\left(\left[\begin{array}{ll}
0.011 & 0
\end{array}\right]\left[\begin{array}{cc}
0.36 & 0.5 \\
0.5 & 1.1
\end{array}\right]\left[\begin{array}{c}
0.011 \\
0
\end{array}\right]+1(0.01)(1)\right)^{-1} \\
&=\left[\begin{array}{c}
0.40 \\
0.55
\end{array}\right]
\end{aligned}
K 1 β β = P Λ 1 β H 1 T β ( H 1 β P Λ 1 β H 1 T β + M 1 β R 1 β M 1 T β ) β 1 = [ 0.36 0.5 β 0.5 1.1 β ] [ 0.011 0 β ] ( [ 0.011 β 0 β ] [ 0.36 0.5 β 0.5 1.1 β ] [ 0.011 0 β ] + 1 ( 0.01 ) ( 1 ) ) β 1 = [ 0.40 0.55 β ] β x ^ 1 = x Λ 1 + K 1 ( y 1 β h 1 ( x Λ 1 , 0 ) ) [ p ^ 1 p Λ ^ 1 ] = [ 2.5 4 ] + [ 0.40 0.55 ] ( 0.52 β 0.49 ) = [ 2.51 4.02 ]
\begin{aligned}
\hat{\mathbf{x}}_{1} &=\check{\mathbf{x}}_{1}+\mathbf{K}_{1}\left(\mathbf{y}_{1}-\mathbf{h}_{1}\left(\check{\mathbf{x}}_{1}, \mathbf{0}\right)\right) \\
{\left[\begin{array}{c}
\hat{p}_{1} \\
\hat{\dot{p}}_{1}
\end{array}\right]}&={\left[\begin{array}{c}
2.5 \\
4
\end{array}\right]+\left[\begin{array}{c}
0.40 \\
0.55
\end{array}\right](0.52-0.49)=\left[\begin{array}{c}
2.51 \\
4.02
\end{array}\right] }
\end{aligned}
x ^ 1 β [ p ^ β 1 β p Λ β ^ β 1 β β ] β = x Λ 1 β + K 1 β ( y 1 β β h 1 β ( x Λ 1 β , 0 ) ) = [ 2.5 4 β ] + [ 0.40 0.55 β ] ( 0.52 β 0.49 ) = [ 2.51 4.02 β ] β P ^ 1 = ( 1 β K 1 H 1 ) P Λ 1 = [ 0.36 0.50 0.50 1.1 ]
\begin{aligned}
\hat{\mathbf{P}}_{1} &=\left(\mathbf{1}-\mathbf{K}_{1} \mathbf{H}_{1}\right) \check{\mathbf{P}}_{1} \\
&=\left[\begin{array}{cc}
0.36 & 0.50 \\
0.50 & 1.1
\end{array}\right]
\end{aligned}
P ^ 1 β β = ( 1 β K 1 β H 1 β ) P Λ 1 β = [ 0.36 0.50 β 0.50 1.1 β ] β Summary The EKF uses linearization to adapt the Kalman Filter to nonlinear systems
Linearization works by computing a local linear apporximation to a nonlinear function using the first-order Taylor expansion on a chosen operating point (in this case, the last state estimate)
Reference 
