Docs
Notes
SI
Understanding
EKF Limitations

EKF Limitations

Linearization Error

Recap: The EKF works by linearizing the nonlinear motion and measurement models to update the mean and covariance of the state.

The difference between the linear approximation and the nonlinear function is called linearization error

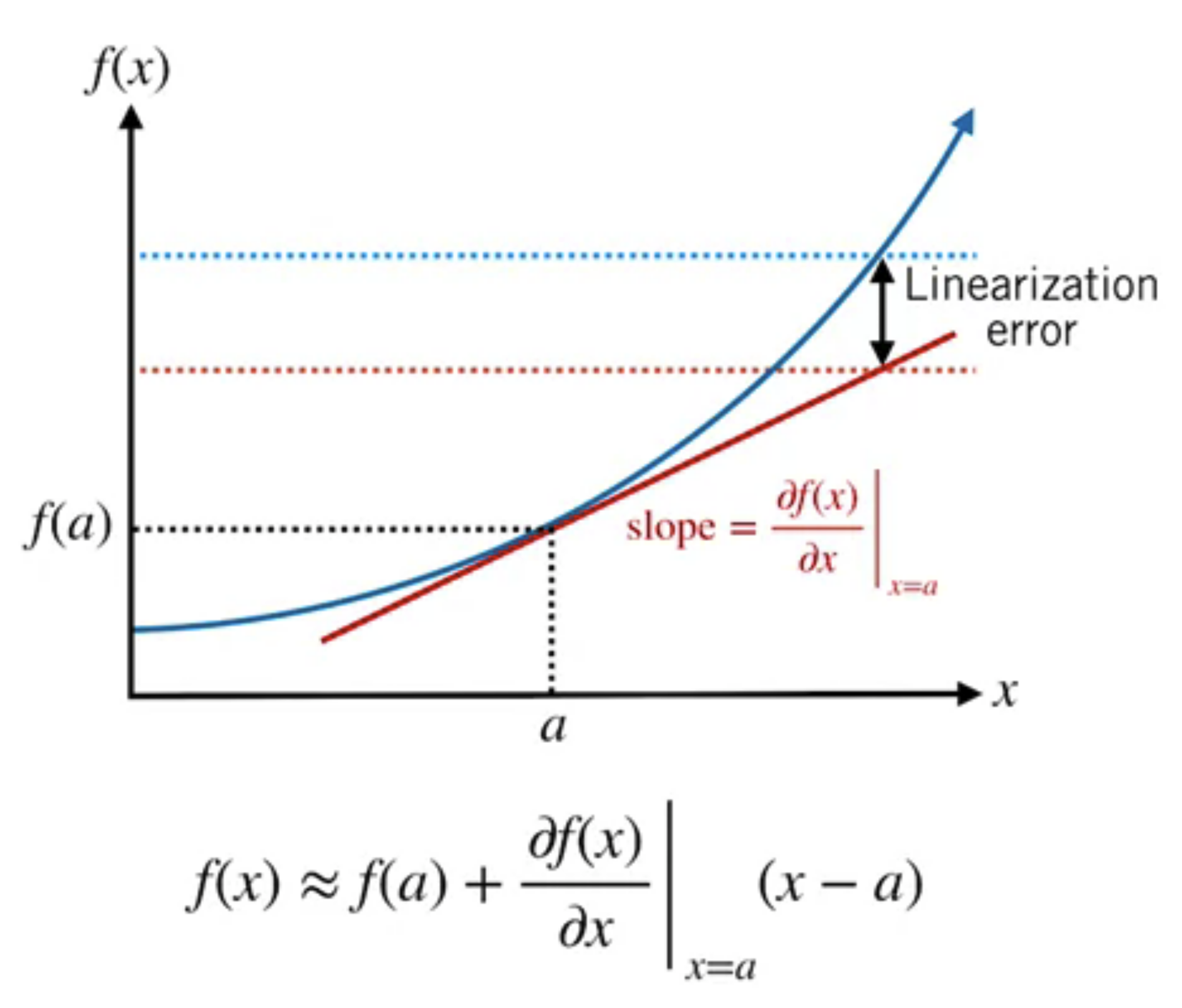
截屏2022-07-21 15.51.52

In general, linearization error depends on

  • How nonlinear the function is
  • How far away from the operating poitn the linear approximation is being used

Example: Polar Coordinates $\rightarrow$ Cartesian Coordinates

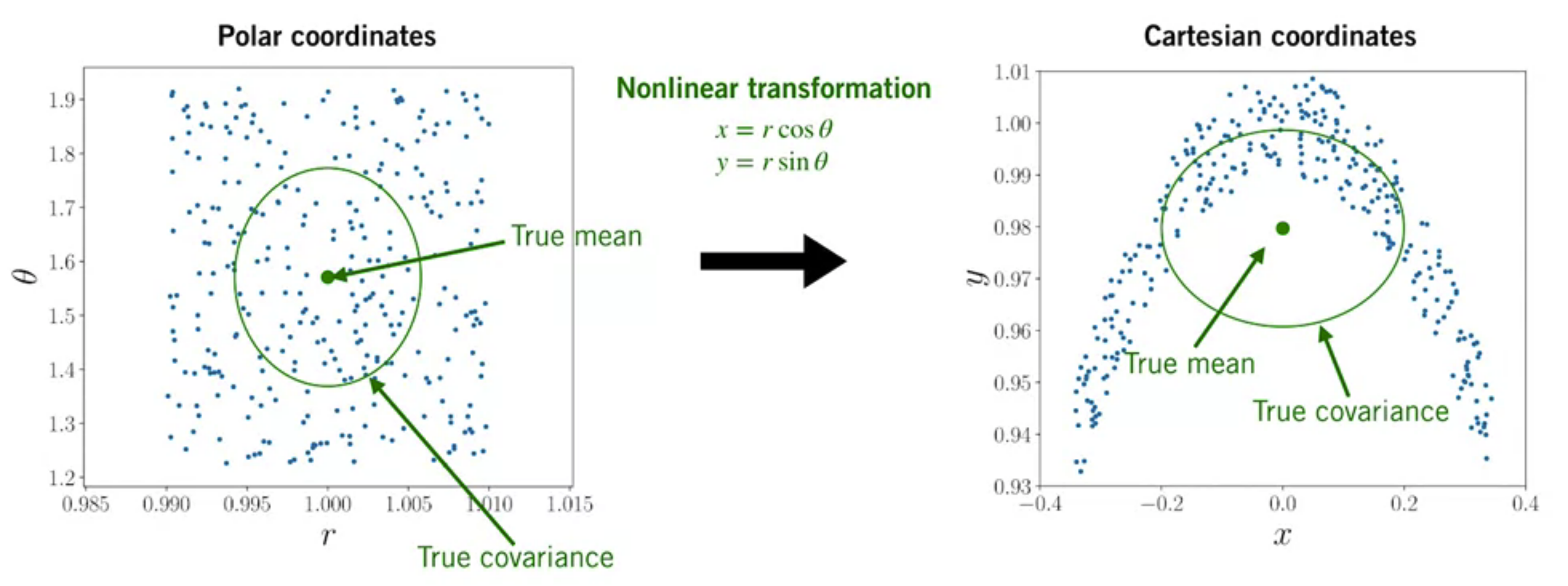
截屏2022-07-21 15.55.56

Now we perform linearized transformation:

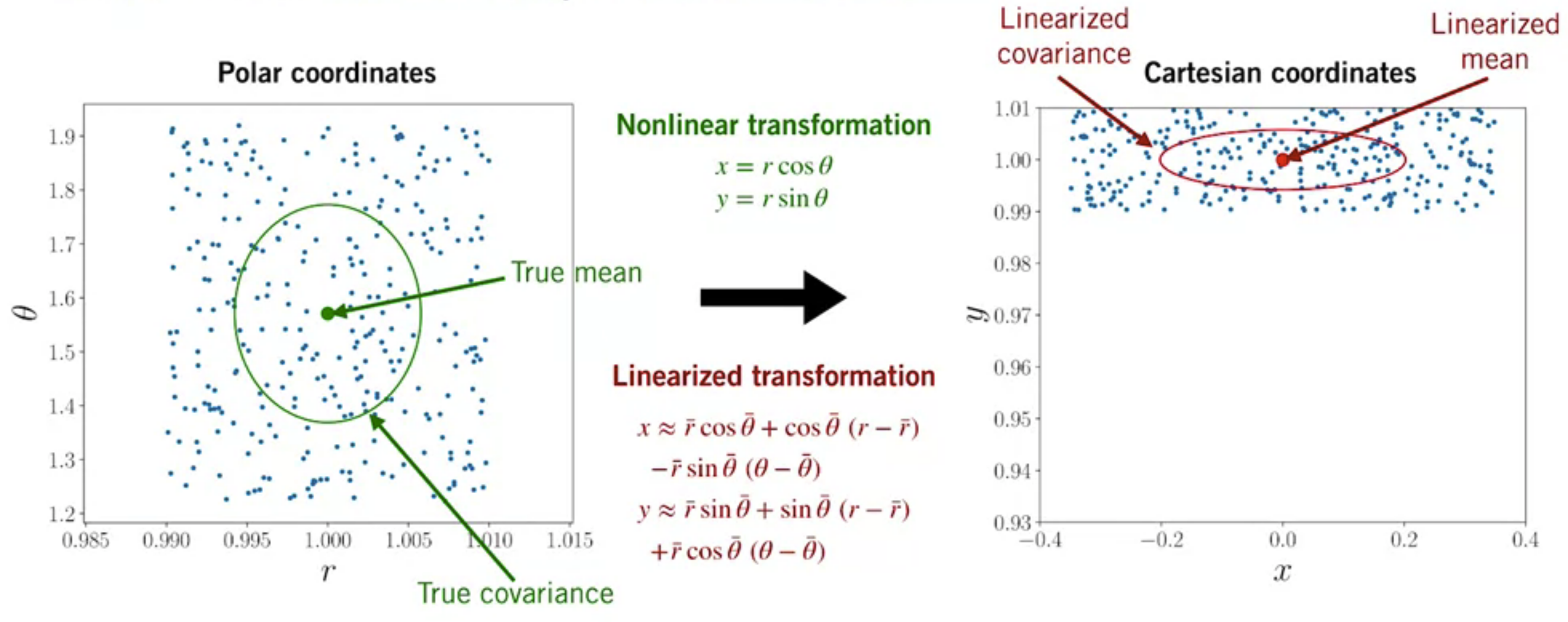
截屏2022-07-21 15.57.09

Compare the linearized and nonlinearized output distributions:

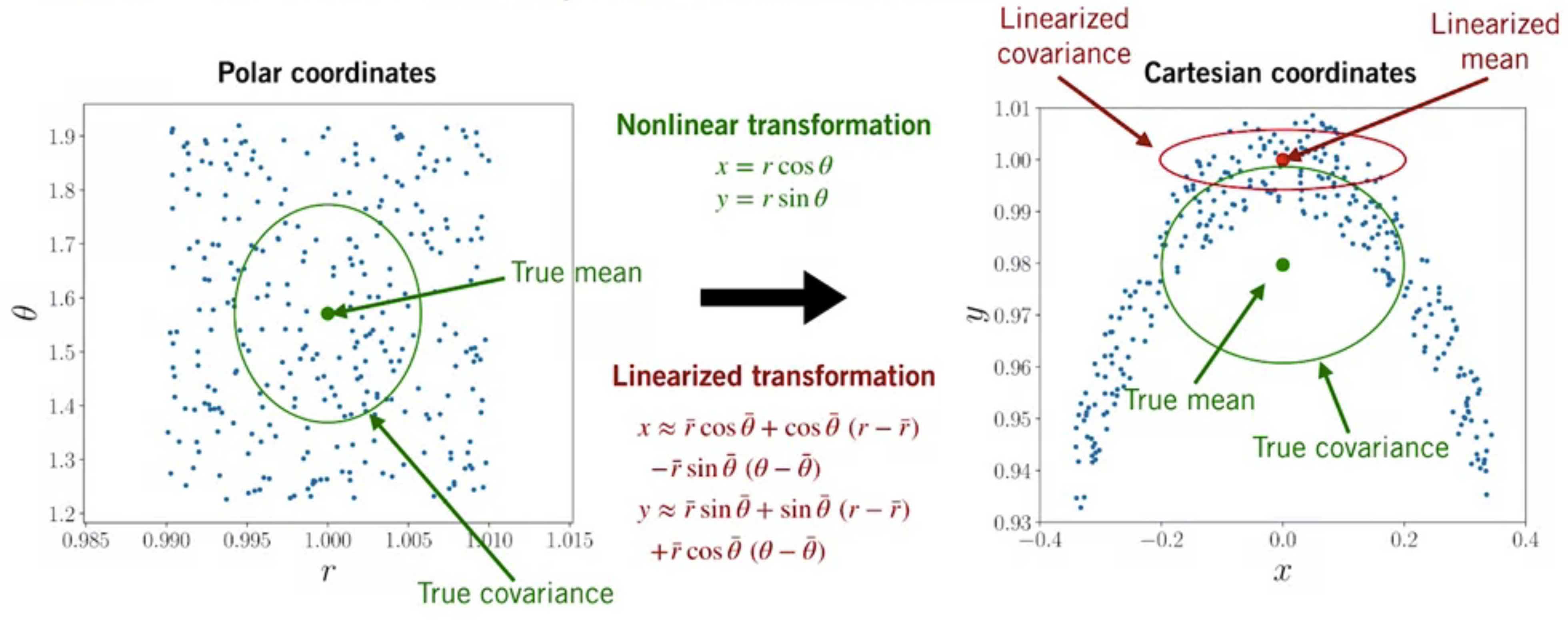
截屏2022-07-21 15.56.53

  • The mean of the linearized distribution is a very different place than the true mean
  • The linearized covariance seriously underestimates the spread of the true output distribution along the $y$-dimension

$\rightarrow$ In this case, the linearization error can cause our belief of the output distribution to completely miss the mark, and this can cause big problem in our estimator!

Limitations of the EKF

Linearization errors

The EKF is prone to linearization error when

  • The system dynamics are highly nonlinear
  • The sensor sampling is slow relative how fast the system is evolving

This has two important consequences

  • The estimated mean state can become very different from the true state
  • The estimated state covariance can fail to capture the true uncertainty in the state

$\Rightarrow$ Linearization error can cause the estimator to be overconfident in a wrong answer!

Computing Jacobians

Computing Jacobian matrices for complicated nonlinear functions is also a common source of error in EKF implementations!

  • Analytical differentiation is prone to human error
  • Numerical differentiation can be slow and unstable
  • Automatic differentiation (e.g., at compile time) can also behave unpredictably

And what if one or more of our models is non-differentiable (e.g. the step function)?

Summary

  • The EKF uses analytical local linearization and, as a result, is sensitive to linearization errors
  • For highly nonlinear systems, the EKF estimate can diverge and become unreliable
  • Computing complex Jacobin matrices is an error-prone process and must be done with substantial care

Reference