Docs
Notes
SI
Understanding
KF Family: ES-EKF

Error State Extended Kalman Filter (ES-EKF)

What’s in a State?

We can think of the vehicle state as composed of two parts

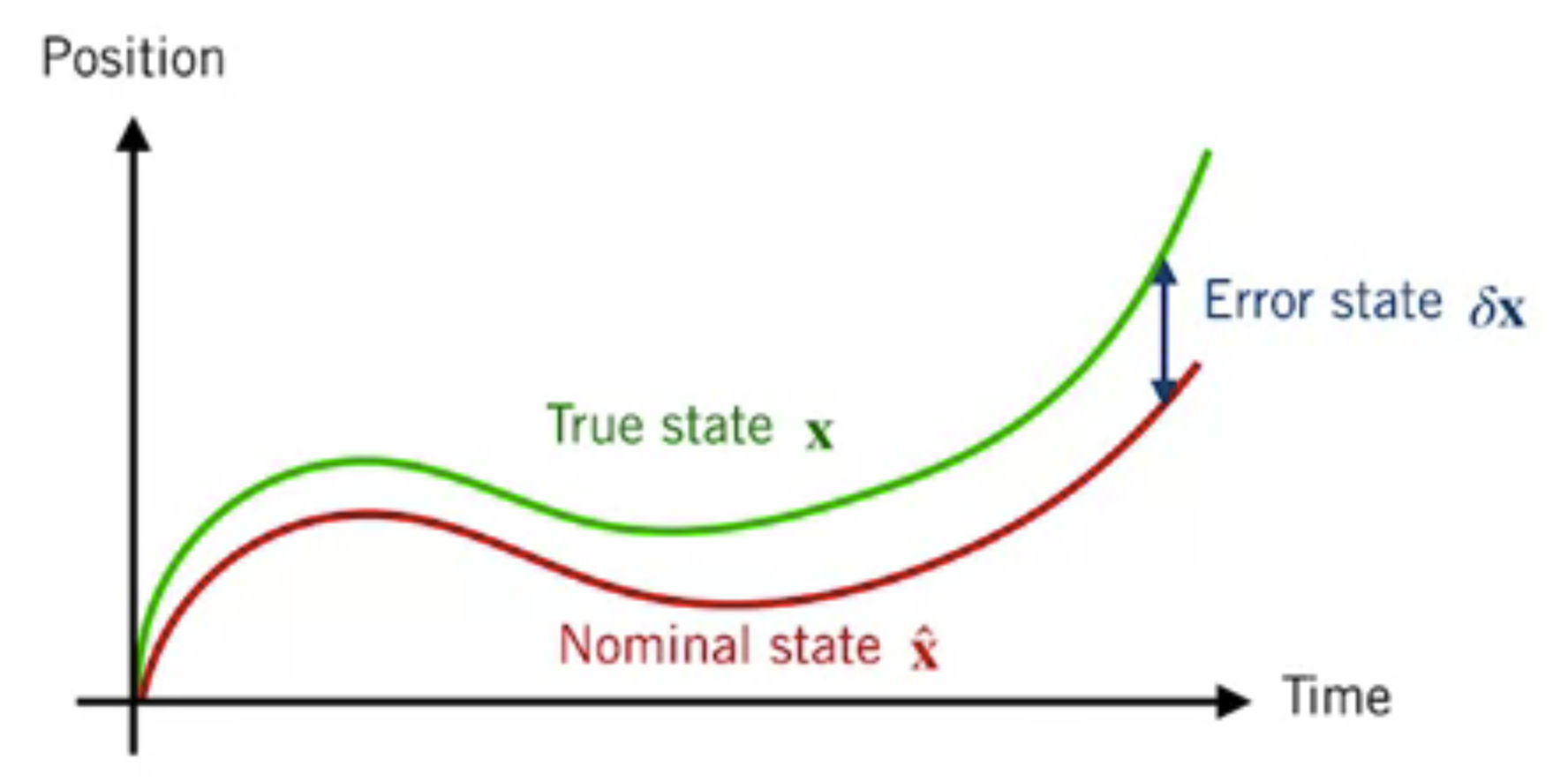
$$ \underbrace{\mathbf{x}}_{\text{True state|}}=\underbrace{\hat{\mathbf{x}}}_{\text{Nominal state ("Large")}}+\underbrace{\delta \mathbf{x}}_{\text{Error state ("small")}} $$ 截屏2022-07-20 22.29.28

💡 Idea

Instead of doing Kalman Filter in the full state (which might have lots of complicated nonlinear behaviours). we use the EKF to directly estimate the error state instead, and then use the estimate of the error state as a correction for nominal state.

截屏2022-07-20 22.33.53

ES-EKF Steps

Loop

  1. Update nominal state with motion model (for a bunch of times until getting the measurement)

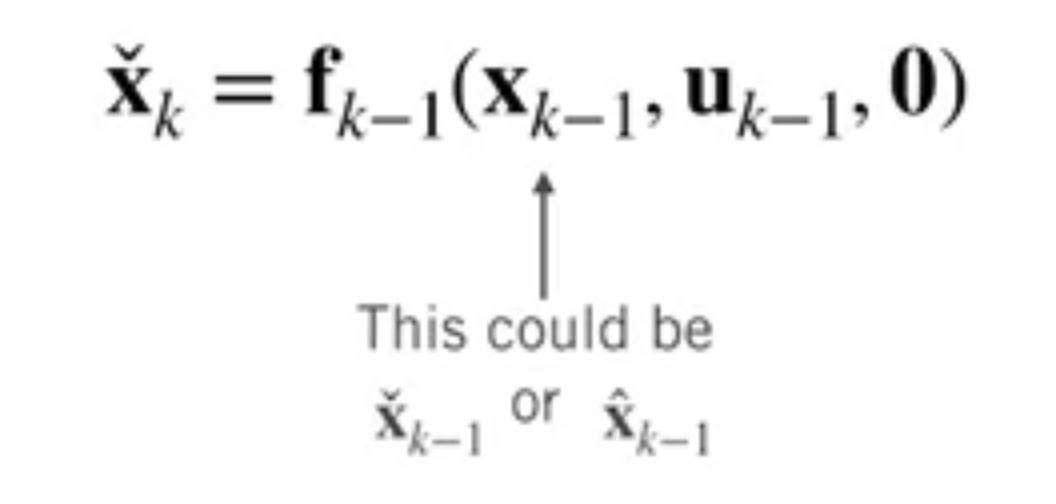
    截屏2022-07-20 22.36.51

  2. Propagate uncertainty (for a bunch of times until getting the measurement)

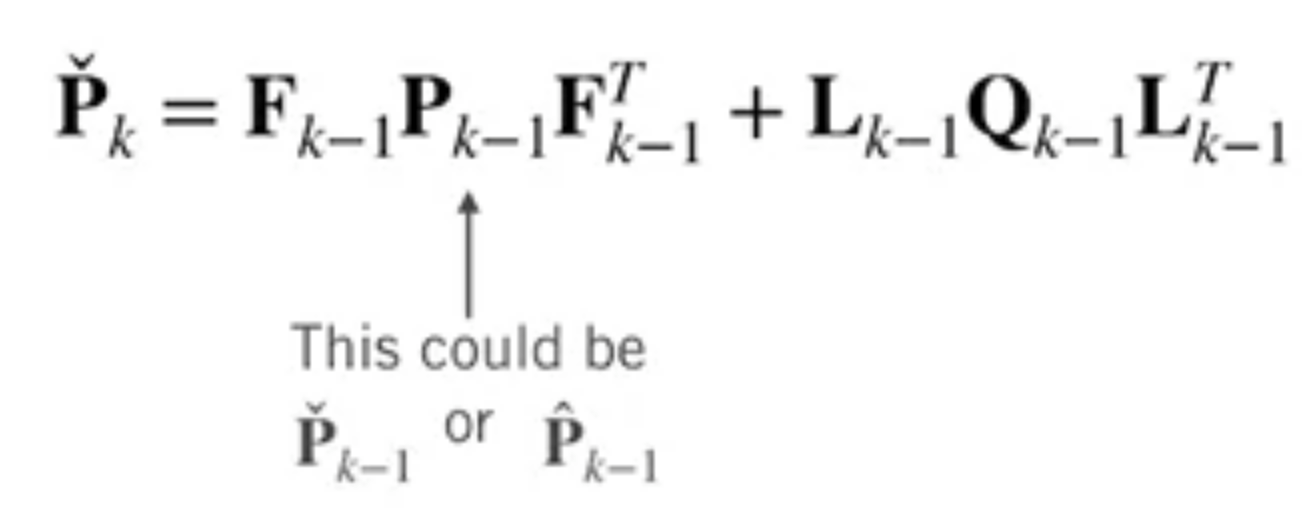
    截屏2022-07-20 22.37.38

  3. If a measurement is available

    1. Compute Kalman Gain

    2. Compute error state

      $$ \delta \hat{\mathbf{x}}_{k}=\mathbf{K}_{k}\left(\mathbf{y}_{k}-\mathbf{h}_{k}\left(\check{\mathbf{x}}_{k}, \mathbf{0}\right)\right) $$

    3. Correct nominal state

      $$ \hat{\mathbf{x}}_{k}=\check{\mathbf{x}}_{k}+\delta \hat{\mathbf{x}}_{k} $$

    4. Correct state covariance

      $$ \hat{\mathbf{P}}_{k}=\left(\mathbf{1}-\mathbf{K}_{k} \mathbf{H}_{k}\right) \check{\mathbf{P}}_{k} $$

Why Use the ES-EKF?

  • Better performance compared to the vanilla EKF

    The “small” error state is more amenable to linear filtering than the “large” nominal state, which can be integrated nonlinearly

  • Easy to work with constrained quantities (e.g. rotations in 3D)

    We can also break down the state using a generalized composition operator

    $$ \underbrace{\mathbf{x}}_{\text{true state}}=\underbrace{\hat{\mathbf{x}}}_{\text{Nominal state (constrained)}} \bigoplus \underbrace{\delta\mathbf{x}}_{\text{Error state (unconstrained)}} $$

Summary

  • The error-state formulation separates the state into a “large” nominal state and a “small” error state

    • nominal state: keeps track of the motion model, predicts what the state should be
    • error state: captures the modeling errors and the process noise that accumulate over time

  • The ES-EKF uses local linearization to estimate the error state and uses it to correct the nominal state

  • The ES-EKF can perform better thant the vanilla EKF, and provides a natural way to handle constrained quantities like 3D rotations

Reference