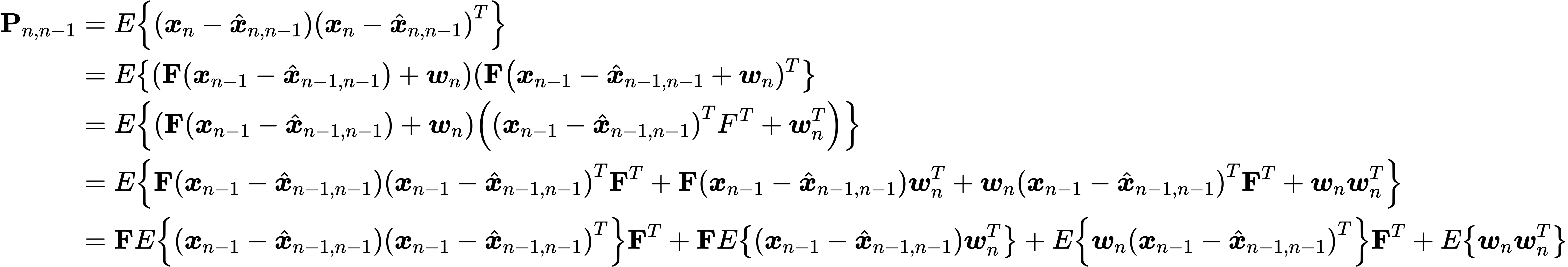Kalman Filter The Kalman filter is an efficient recursive filter estimating the internal-state of a linear dynamic system from a series of noisy measurements.
Applications of Kalman filter include
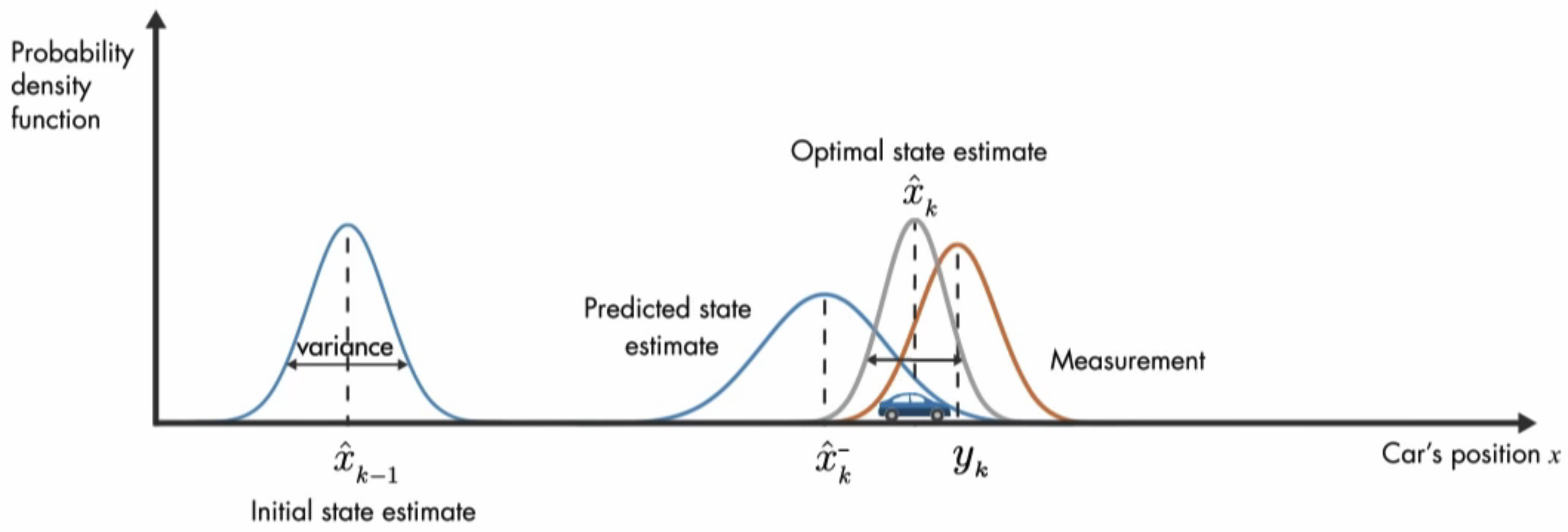
Guidance Navigation Control of vehicles, aircraft, spacecraft, and ships positioned dynamically π‘ The basic idea of Kalman filter is to achieve the optimal estimate of the (hidden) internal state by weightedly combining the state prediction and the measurement .
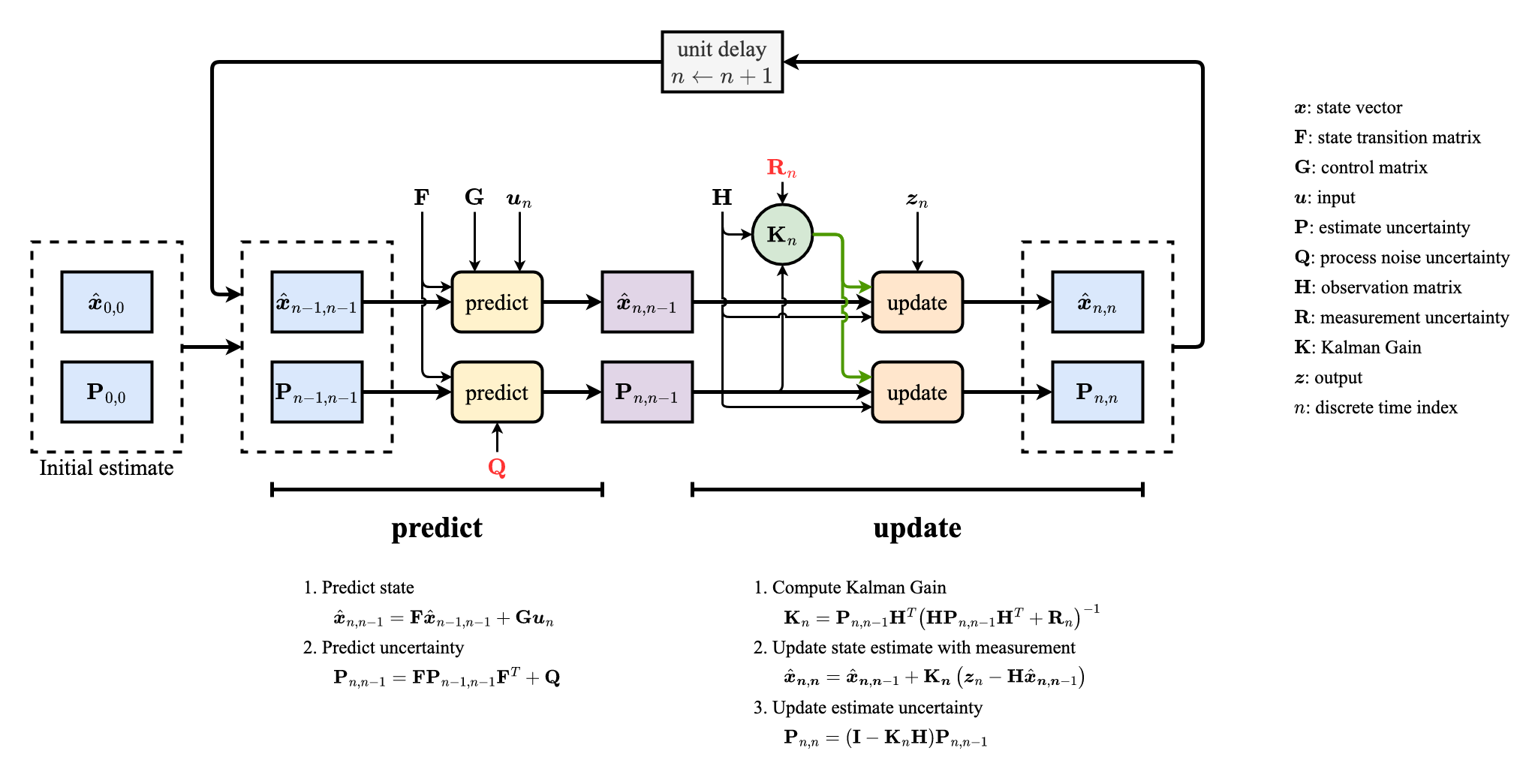
Kalman Filter Summary Kalman filter in a picture:
Summary of equations:
Equation Equation Name Alternative Names Predict x ^ n , n β 1 = F x ^ n β 1 , n β 1 + G u n \hat{\boldsymbol{x}}_{n, n-1}=\mathbf{F} \hat{\boldsymbol{x}}_{n-1, n-1} + \mathbf{G} \boldsymbol{u}_{n} x ^ n , n β 1 β = F x ^ n β 1 , n β 1 β + G u n β State Extrapolation Predictor Equation P n , n β 1 = F P n β 1 , n β 1 F T + Q \mathbf{P}_{n, n-1}=\mathbf{F} \mathbf{P}_{n-1, n-1} \mathbf{F}^{T}+\mathbf{Q} P n , n β 1 β = F P n β 1 , n β 1 β F T + Q Covariance Extrapolation Predictor Covariance Equation Update K n = P n , n β 1 H T ( H P n , n β 1 H T + R n ) β 1 \mathbf{K}_{n}=\mathbf{P}_{n, n-1} \mathbf{H}^{T}\left(\mathbf{H} \mathbf{P}_{n, n-1} \mathbf{H}^{T}+\mathbf{R}_{n}\right)^{-1} K n β = P n , n β 1 β H T ( H P n , n β 1 β H T + R n β ) β 1 Kalman Gain Weight Equation x ^ n , n = x ^ n , n β 1 + K n ( z n β H x ^ n , n β 1 ) \hat{\boldsymbol{x}}_{\boldsymbol{n}, \boldsymbol{n}}=\hat{\boldsymbol{x}}_{\boldsymbol{n}, \boldsymbol{n}-1}+\mathbf{K}_{\boldsymbol{n}}\left(\boldsymbol{z}_{n}-\mathbf{H} \hat{\boldsymbol{x}}_{\boldsymbol{n}, \boldsymbol{n}-1}\right) x ^ n , n β = x ^ n , n β 1 β + K n β ( z n β β H x ^ n , n β 1 β ) State Update Filtering Equation P n , n = ( I β K n H ) P n , n β 1 \mathbf{P}_{n, n}=\left(\mathbf{I}-\mathbf{K}_{n} \mathbf{H}\right) \mathbf{P}_{n, n-1} P n , n β = ( I β K n β H ) P n , n β 1 β Covariance Update Corrector Equation Auxilliary z n = H x n + v n \boldsymbol{z}_{n} = \mathbf{H} \boldsymbol{x}_n + \boldsymbol{v}_n z n β = H x n β + v n β Measurement Equation R n = E { v n v n T } \mathbf{R}_n = E\{\boldsymbol{v}_n \boldsymbol{v}_n^T\} R n β = E { v n β v n T β } Measurement Uncertainty Measurement Error Q n = E { w n w n T } \mathbf{Q}_n = E\{\boldsymbol{w}_n \boldsymbol{w}_n^T\} Q n β = E { w n β w n T β } Process Noise Uncertainty Process Noise Error P n , n = E { e n e n T } = E { ( x n β x ^ n , n ) ( x n β x ^ n , n ) T } \mathbf{P}_{n, n}=E\left\{\boldsymbol{e}_{n} \boldsymbol{e}_{n}^{T}\right\}=E\left\{\left(\boldsymbol{x}_{n}-\hat{\boldsymbol{x}}_{n, n}\right)\left(\boldsymbol{x}_{n}-\hat{\boldsymbol{x}}_{n, n}\right)^{T}\right\} P n , n β = E { e n β e n T β } = E { ( x n β β x ^ n , n β ) ( x n β β x ^ n , n β ) T } Estimation Uncertainty Estimation Error
Summary of notations:
Term Name Alternative Term x \boldsymbol{x} x State vector z \boldsymbol{z} z Output vector y \boldsymbol{y} y F \mathbf{F} F State transition matrix Ξ¦ \mathbf{\Phi} Ξ¦ A \mathbf{A} A u \boldsymbol{u} u Input variable G \mathbf{G} G Control matrix B \boldsymbol{B} B P \mathbf{P} P Estimate uncertainty Ξ£ \boldsymbol{\Sigma} Ξ£ Q \mathbf{Q} Q Process noise uncertainty R \mathbf{R} R Measurement uncertainty w \boldsymbol{w} w Process noise vector v \boldsymbol{v} v Measurement noise vector H \mathbf{H} H Observation matrix C \mathbf{C} C K \mathbf{K} K Kalman Gain n n n Discrete time index k k k
Multidimensional Kalman Filter in Detail A Kalman filter works by a two-phase process, including 5 main equations:
Predict phase: produces prediction of the current state, along with thier uncertaintiesUpdate phase: checks how good the predicted result fits to the current measurement and refines the state prediction using a weighted average given measurements if necessary.The Kalman filter assumes that the true state of a system at time step n n n n β 1 n-1 n β 1
x n = F x n β 1 + G u n + w n
\boldsymbol{x}_n = \mathbf{F} \boldsymbol{x}_{n-1} +\mathbf{G} \boldsymbol{u}_{n} + \boldsymbol{w}_n
x n β = F x n β 1 β + G u n β + w n β x n \boldsymbol{x}_{n} x n β state vector
u n \boldsymbol{u}_{n} u n β control variable or input variable - a measurable (deterministic) input to the system
w n \boldsymbol{w}_n w n β process noise or disturbance - an unmeasurable input that affects the state
F \mathbf{F} F state transition matrix - applies the effect of each system state parameter at time step n β 1 n-1 n β 1 n n n
G \mathbf{G} G control matrix or input transition matrix (mapping control to state variables)
The state extrapolation equation
Predicts the next system state, based on the knowledge of the current state
Extrapolates the state vector from time step n β 1 n-1 n β 1 n n n
Also called
Predictor Equation Transition Equation Prediction Equation Dynamic Model State Space Model The general form in a matrix notation
x ^ n , n β 1 = F x ^ n β 1 , n β 1 + G u n
\hat{\boldsymbol{x}}_{n, n-1}=\mathbf{F} \hat{\boldsymbol{x}}_{n-1, n-1}+\mathbf{G} \boldsymbol{u}_{n}
x ^ n , n β 1 β = F x ^ n β 1 , n β 1 β + G u n β x ^ n , n β 1 \hat{\boldsymbol{x}}_{n, n-1} x ^ n , n β 1 β n n n
x ^ n β 1 , n β 1 \hat{\boldsymbol{x}}_{n-1, n-1} x ^ n β 1 , n β 1 β n β 1 n-1 n β 1
x ^ n , m \hat{\boldsymbol{x}}_{n, m} x ^ n , m β x \boldsymbol{x} x n n n m β€ n m \leq n m β€ n
Example The covariance extrapolation equation extrapolates the uncertainty in our state prediction .
P n , n β 1 = F P n β 1 , n β 1 F T + Q
\mathbf{P}_{n, n-1}=\mathbf{F} \mathbf{P}_{n-1, n-1} \mathbf{F}^{T}+\mathbf{Q}
P n , n β 1 β = F P n β 1 , n β 1 β F T + Q P n β 1 , n β 1 \mathbf{P}_{n-1, n-1} P n β 1 , n β 1 β n β 1 n-1 n β 1
P n β 1 , n β 1 = E { ( x n β 1 , n β 1 β x ^ n β 1 , n β 1 ) β = : e n ( x n β 1 , n β 1 β x ^ n β 1 , n β 1 ) T } = E { e n e n T }
\begin{aligned}
\mathbf{P}_{n-1, n-1} &= E\{\underbrace{(\boldsymbol{x}_{n-1, n-1} - \hat{\boldsymbol{x}}_{n-1, n-1})}_{=: \boldsymbol{e}_n} (\boldsymbol{x}_{n-1, n-1} - \hat{\boldsymbol{x}}_{n-1, n-1}) ^T\} \\
& = E\{\boldsymbol{e}_n \boldsymbol{e}_n^T\}
\end{aligned}
P n β 1 , n β 1 β β = E { =: e n β ( x n β 1 , n β 1 β β x ^ n β 1 , n β 1 β ) β β ( x n β 1 , n β 1 β β x ^ n β 1 , n β 1 β ) T } = E { e n β e n T β } β P n , n β 1 \mathbf{P}_{n, n-1} P n , n β 1 β n n n
F \mathbf{F} F
Q \mathbf{Q} Q
Q n = E { w n w n T }
\mathbf{Q}_n = E\{\boldsymbol{w}_n \boldsymbol{w}_n^T\}
Q n β = E { w n β w n T β } w n \boldsymbol{w}_n w n β Derivation At time step n n n
x _ n = F x _ n β 1 + G u _ n + w _ n
\boldsymbol{x}\_n = \mathbf{F} \boldsymbol{x}\_{n-1} +\mathbf{G} \boldsymbol{u}\_{n} + \boldsymbol{w}\_n
x _ n = F x _ n β 1 + G u _ n + w _ n The prediction of state is
x ^ _ n , n β 1 = F x ^ _ n β 1 , n β 1 + G u _ n
\hat{\boldsymbol{x}}\_{n, n-1}=\mathbf{F} \hat{\boldsymbol{x}}\_{n-1, n-1}+\mathbf{G} \boldsymbol{u}\_{n}
x ^ _ n , n β 1 = F x ^ _ n β 1 , n β 1 + G u _ n The difference between x _ n \boldsymbol{x}\_n x _ n x ^ _ n , n β 1 \hat{\boldsymbol{x}}\_{n, n-1} x ^ _ n , n β 1
x _ n β x ^ _ n , n β 1 = F x _ n β 1 + G u _ n + w _ n β ( F x ^ _ n β 1 , n β 1 + G u _ n ) = F ( x _ n β 1 β x ^ _ n β 1 , n β 1 ) + w _ n
\begin{aligned}
\boldsymbol{x}\_{n}-\hat{\boldsymbol{x}}\_{n, n-1} &=\mathbf{F} \boldsymbol{x}\_{n-1}+\mathbf{G} \boldsymbol{u}\_{n}+\boldsymbol{w}\_{n}-\left(\mathbf{F} \hat{\boldsymbol{x}}\_{n-1, n-1}+\mathbf{G} \boldsymbol{u}\_{n}\right) \\\\
&=\mathbf{F}\left(\boldsymbol{x}\_{n-1}-\hat{\boldsymbol{x}}\_{n-1, n-1}\right)+\boldsymbol{w}\_{n}
\end{aligned}
x _ n β x ^ _ n , n β 1 β = F x _ n β 1 + G u _ n + w _ n β ( F x ^ _ n β 1 , n β 1 + G u _ n ) = F ( x _ n β 1 β x ^ _ n β 1 , n β 1 ) + w _ n β The variance associate with the prediction x ^ _ n , n β 1 \hat{\boldsymbol{x}}\_{n, n-1} x ^ _ n , n β 1 x _ n \boldsymbol{x}\_n x _ n
Noting that the state estimation errors and process noise are uncorrelated:
E\left\\{\left(\boldsymbol{x}\_{n-1}-\hat{\boldsymbol{x}}\_{n-1, n-1}\right) \boldsymbol{w}\_{n}^{T}\right\\} = E\left\\{\boldsymbol{w}\_{n}\left(\boldsymbol{x}\_{n-1}-\hat{\boldsymbol{x}}\_{n-1, n-1}\right)^{T}\right\\} = 0
Therefore
\begin{aligned}
\mathbf{P}\_{n, n-1} &=\underbrace{E\left\\{\left(\boldsymbol{x}\_{n-1}-\hat{\boldsymbol{x}}\_{n-1, n-1}\right)\left(\boldsymbol{x}\_{n-1}-\hat{\boldsymbol{x}}\_{n-1, n-1}\right)^{T}\right\\}}\_{=\mathbf{P}\_{n-1, n-1}} \mathbf{F}^{T}+\underbrace{E\left\\{w\_{n} w\_{n}^{T}\right\\}}\_{=\mathbf{Q}} \\\\
&=\mathbf{F} \mathbf{P}\_{n-1, n-1}\mathbf{F}^T+\mathbf{Q}
\end{aligned}
Kalman Gain equation The Kalman Gain is calculated so that it minimizes the covariance of the a posteriori state estimate.
K n = P n , n β 1 H T ( H P n , n β 1 H T + R n ) β 1
\mathbf{K}_{n}=\mathbf{P}_{n, n-1} \mathbf{H}^{T}\left(\mathbf{H} \mathbf{P}_{n, n-1} \mathbf{H}^{T}+\mathbf{R}_{n}\right)^{-1}
K n β = P n , n β 1 β H T ( H P n , n β 1 β H T + R n β ) β 1 Derivation Rearrange the covariance update equation
P _ n , n = ( I β K _ n H ) P _ n , n β 1 ( I β K _ n H ) T + K _ n R _ n K _ n T P _ n , n = ( I β K _ n H ) P _ n , n β 1 ( I β ( K _ n H ) T ) + K _ n R _ n K _ n T β£ I = I T P _ n , n = ( I β K _ n H ) P _ n , n β 1 ( I β H T K _ n T ) + K _ n R _ n K _ n T β£ ( A B ) T = B T A T P _ n , n = ( P _ n , n β 1 β K _ n H P _ n , n β 1 ) ( I β H T K _ n T ) + K _ n R _ n K _ n T P _ n , n = P _ n , n β 1 β P _ n , n β 1 H T K _ n T β K _ n H P _ n , n β 1 + K _ n H P _ n , n β 1 H T K _ n T + K _ n R _ n K _ n T β£ A B A T + A C A T = A ( B + C ) A T P _ n , n = P _ n , n β 1 β P _ n , n β 1 H T K _ n T β K _ n H P _ n , n β 1 + K _ n ( H P _ n , n β 1 H T + R _ n ) K _ n T
\begin{array}{l}
\mathbf{P}\_{n, n}=\left(\mathbf{I}-\mathbf{K}\_{n} \mathbf{H}\right) \mathbf{P}\_{n, n-1}{\color{DodgerBlue} \left(\mathbf{I}-\mathbf{K}\_{n} \mathbf{H}\right)^{T}}+\mathbf{K}\_{n} \mathbf{R}\_{n} \mathbf{K}\_{n}^{T} \\\\\\\\
\mathbf{P}\_{n, n}=\left(\mathbf{I}-\mathbf{K}\_{n} \mathbf{H}\right) \mathbf{P}\_{n, n-1}{\color{DodgerBlue}\left(\mathbf{I}-\left(\mathbf{K}\_{n} \mathbf{H}\right)^{T}\right)}+\mathbf{K}\_{n} \mathbf{R}\_{n} \mathbf{K}\_{n}^{T} \qquad | \text{ } \mathbf{I} = \mathbf{I}^T \\\\\\\\
\mathbf{P}\_{n, n}={\color{ForestGreen}\left(\mathbf{I}-\mathbf{K}\_{n} \mathbf{H}\right) \mathbf{P}\_{n, n-1}}{\color{DodgerBlue}\left(\mathbf{I}-\mathbf{H}^{T} \mathbf{K}\_{n}^{T}\right)}+\mathbf{K}\_{n} \mathbf{R}\_{n} \mathbf{K}\_{n}^{T} \qquad | \text{ } (\mathbf{AB})^T = \mathbf{B}^T \mathbf{A}^T\\\\\\\\
\mathbf{P}\_{n, n}={\color{ForestGreen}\left(\mathbf{P}\_{n, n-1}-\mathbf{K}\_{n} \mathbf{H} \mathbf{P}\_{n, n-1}\right)}\left(\mathbf{I}-\mathbf{H}^{T} \mathbf{K}\_{n}^{T}\right)+\mathbf{K}\_{n} \mathbf{R}\_{n} \mathbf{K}\_{n}^{T} \\\\\\\\
\mathbf{P}\_{n, n}=\mathbf{P}\_{n, n-1}-\mathbf{P}\_{n, n-1} \mathbf{H}^{T} \mathbf{K}\_{n}^{T}-\mathbf{K}\_{n} \mathbf{H} \mathbf{P}\_{n, n-1} \\\\
+{\color{MediumOrchid}\mathbf{K}\_{n} \mathbf{H} \mathbf{P}\_{n, n-1} \mathbf{H}^{T} \mathbf{K}\_{n}^{T}+\mathbf{K}\_{n} \mathbf{R}\_{n} \mathbf{K}\_{n}^{T}} \qquad | \text{ } \mathbf{AB}\mathbf{A}^T + \mathbf{AC}\mathbf{A}^T = \mathbf{A}(\mathbf{B} + \mathbf{C})\mathbf{A}^T
\\\\\\\\
\mathbf{P}\_{n, n}=\mathbf{P}\_{n, n-1}-\mathbf{P}\_{n, n-1} \mathbf{H}^{T} \mathbf{K}\_{n}^{T}-\mathbf{K}\_{n} \mathbf{H} \mathbf{P}\_{n, n-1} \\\\
+{\color{MediumOrchid}\mathbf{K}\_{n}\left(\mathbf{H} \mathbf{P}\_{n, n-1} \mathbf{H}^{T}+\boldsymbol{\mathbf{R}}\_{n}\right) \mathbf{K}\_{n}^{T}}
\end{array}
P _ n , n = ( I β K _ n H ) P _ n , n β 1 ( I β K _ n H ) T + K _ n R _ n K _ n T P _ n , n = ( I β K _ n H ) P _ n , n β 1 ( I β ( K _ n H ) T ) + K _ n R _ n K _ n T β£ I = I T P _ n , n = ( I β K _ n H ) P _ n , n β 1 ( I β H T K _ n T ) + K _ n R _ n K _ n T β£ ( AB ) T = B T A T P _ n , n = ( P _ n , n β 1 β K _ n HP _ n , n β 1 ) ( I β H T K _ n T ) + K _ n R _ n K _ n T P _ n , n = P _ n , n β 1 β P _ n , n β 1 H T K _ n T β K _ n HP _ n , n β 1 + K _ n HP _ n , n β 1 H T K _ n T + K _ n R _ n K _ n T β£ AB A T + AC A T = A ( B + C ) A T P _ n , n = P _ n , n β 1 β P _ n , n β 1 H T K _ n T β K _ n HP _ n , n β 1 + K _ n ( HP _ n , n β 1 H T + R _ n ) K _ n T β As the Kalman Filter is an optimal filter , we will seek a Kalman Gain that minimizes the estimate variance.
In order to minimize the estimate variance, we need to minimize the main diagonal (from the upper left to the lower right) of the covariance matrix P _ n , n \mathbf{P}\_{n, n} P _ n , n
The sum of the main diagonal of the square matrix is the trace of the matrix. Thus, we need to minimize t r ( P _ n , n ) tr(\mathbf{P}\_{n, n}) t r ( P _ n , n ) t r ( P _ n , n ) tr(\mathbf{P}\_{n, n}) t r ( P _ n , n ) K _ n \mathbf{K}\_n K _ n
t r ( P _ n , n ) = t r ( P _ n , n β 1 ) β t r ( P _ n , n β 1 H T K _ n T ) β t r ( K _ n H P _ n , n β 1 ) + t r ( K _ n ( H P _ n , n β 1 H T + R _ n ) K _ n T ) β£ t r ( A ) = t r ( A T ) t r ( P _ n , n ) = t r ( P _ n , n β 1 ) β 2 t r ( K _ n H P _ n , n β 1 ) + t r ( K _ n ( H P _ n , n β 1 H T + R _ n ) K _ n T ) d d K _ n t r ( P _ n , n ) = d d K _ n t r ( P _ n , n β 1 ) β d d K _ n 2 t r ( K _ n H P _ n , n β 1 ) + d t r ( K _ n ( H P _ n , n β 1 H T + R _ n ) K _ n T ) d K _ n = ! 0 β£ d d A t r ( A B ) = B T , d d A t r ( A B A T ) = 2 A B d ( t r ( P _ n , n ) ) d K _ n = 0 β 2 ( H P _ n , n β 1 ) T + 2 K _ n ( H P _ n , n β 1 H T + R _ n ) = 0 ( H P _ n , n β 1 ) T = K _ n ( H P _ n , n β 1 H T + R _ n ) K _ n = ( H P _ n , n β 1 ) T ( H P _ n , n β 1 H T + R _ n ) β 1 β£ ( A B ) T = B T A T K _ n = P _ n , n β 1 T H T ( H P _ n , n β 1 H T + R _ n ) β 1 β£ covariance matrix P symmetric ( P T = P ) K _ n = P _ n , n β 1 H T ( H P _ n , n β 1 H T + R _ n ) β 1
\begin{array}{l}
tr\left(\mathbf{P}\_{\boldsymbol{n}, \boldsymbol{n}}\right)=tr\left(\mathbf{P}\_{\boldsymbol{n}, \boldsymbol{n}-1}\right)-{\color{DarkOrange}tr\left(\mathbf{P}\_{n, n-1} \mathbf{H}^{T} \mathbf{K}\_{n}^{T}\right)}\\\\
{\color{DarkOrange} -tr\left(\mathbf{K}\_{n} \mathbf{H} \mathbf{P}\_{n, n-1}\right)} + tr\left(\mathbf{K}\_{\boldsymbol{n}}\left(\mathbf{H} \mathbf{P}\_{\boldsymbol{n}, \boldsymbol{n}-\mathbf{1}} \mathbf{H}^{\boldsymbol{T}}+\mathbf{R}\_{\boldsymbol{n}}\right) \mathbf{K}\_{n}^{\boldsymbol{T}}\right) \qquad | \text{} tr(\mathbf{A}) = tr(\mathbf{A}^T)\\\\\\\\
tr\left(\mathbf{P}\_{n, n}\right)=tr\left(\mathbf{P}\_{n, n-1}\right)-{\color{DarkOrange}2 tr\left(\mathbf{K}\_{n} \mathbf{H} \mathbf{P}\_{n, n-1}\right)}\\\\
+tr\left(\mathbf{K}\_{n}\left(\mathbf{H} \mathbf{P}\_{n, n-1} \mathbf{H}^{\boldsymbol{T}}+\mathbf{R}\_{n}\right) \mathbf{K}\_{n}^{T}\right)\\\\\\\\
\frac{d}{d \mathbf{K}\_{n}}t r\left(\mathbf{P}\_{n, n}\right)={\color{DodgerBlue} \frac{d}{d \mathbf{K}\_{n}}t r\left(\mathbf{P}\_{n, n-1}\right)}-{\color{ForestGreen}\frac{d }{d \mathbf{K}\_{n}}2 t r\left(\mathbf{K}\_{n} \mathbf{H} \mathbf{P}\_{n, n-1}\right)} \\\\
+{\color{MediumOrchid}\frac{d tr(\mathbf{K}\_{n}(\mathbf{H}\mathbf{P}\_{n, n-1}\mathbf{H}^T + \mathbf{R}\_n)\mathbf{K}\_{n}^T)}{d\mathbf{K}\_{n}}} \overset{!}{=} 0 \quad \mid {\color{ForestGreen} \frac{d}{d \mathbf{A}}tr(\mathbf{A} \mathbf{B}) = \mathbf{B}^T},{\color{MediumOrchid} \frac{d}{d \mathbf{A}}tr(\mathbf{A} \mathbf{B} \mathbf{A}^T) = 2\mathbf{A} \mathbf{B}}\\\\\\\\
\frac{d\left(t r\left(\mathbf{P}\_{n, n}\right)\right)}{d \mathbf{K}\_{n}}={\color{DodgerBlue}0}-{\color{ForestGreen}2\left(\mathbf{H} \mathbf{P}\_{ n , n - 1 }\right)^{T}}\\\\
+{\color{MediumOrchid}2 \mathbf{K}\_{n}\left(\mathbf{H} \mathbf{P}\_{n, n-1} \mathbf{H}^{T}+\mathbf{R}\_{n}\right)}=0\\\\\\\\
{\color{ForestGreen}\left(\mathbf{H} \mathbf{P}\_{n, n-1}\right)^{T}}={\color{MediumOrchid}\mathbf{K}\_{n}\left(\mathbf{H} \mathbf{P}\_{n, n-1} \mathbf{H}^{T}+\mathbf{R}\_{n}\right)} \\\\\\\\
\mathbf{K}\_{n}=\left(\mathbf{H} \mathbf{P}\_{n, n-1}\right)^{T}\left(\mathbf{H} \mathbf{P}\_{n, n-1} \mathbf{H}^{T}+\mathbf{R}\_{n}\right)^{-1} \quad \mid (\mathbf{AB})^T = \mathbf{B}^T \mathbf{A}^T \\\\\\\\
\mathbf{K}\_{n}=\mathbf{P}\_{n, n-1}^{T} \mathbf{H}^{T}\left(\mathbf{H} \mathbf{P}\_{n, n-1} \mathbf{H}^{T}+\mathbf{R}\_{n}\right)^{-1} \quad | \text{ covariance matrix } \mathbf{P} \text{ symmetric } (\mathbf{P}^T = \mathbf{P})\\\\\\\\
\mathbf{K}\_{n}=\mathbf{P}\_{n, n-1} \mathbf{H}^{T}\left(\mathbf{H} \mathbf{P}\_{n, n-1} \mathbf{H}^{T}+\mathbf{R}\_{n}\right)^{-1}
\end{array}
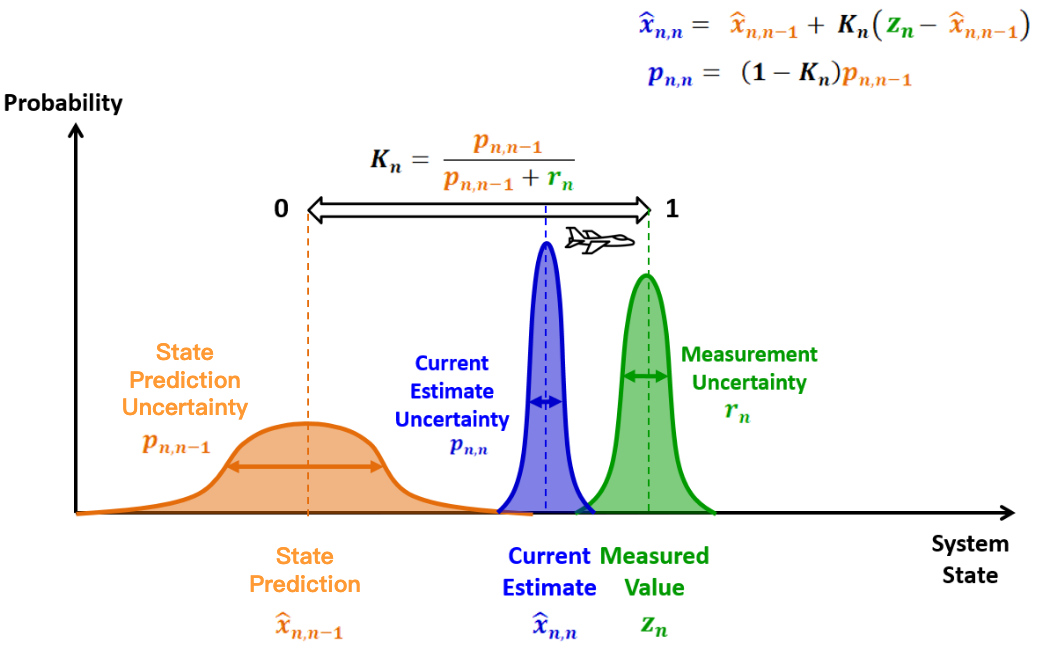
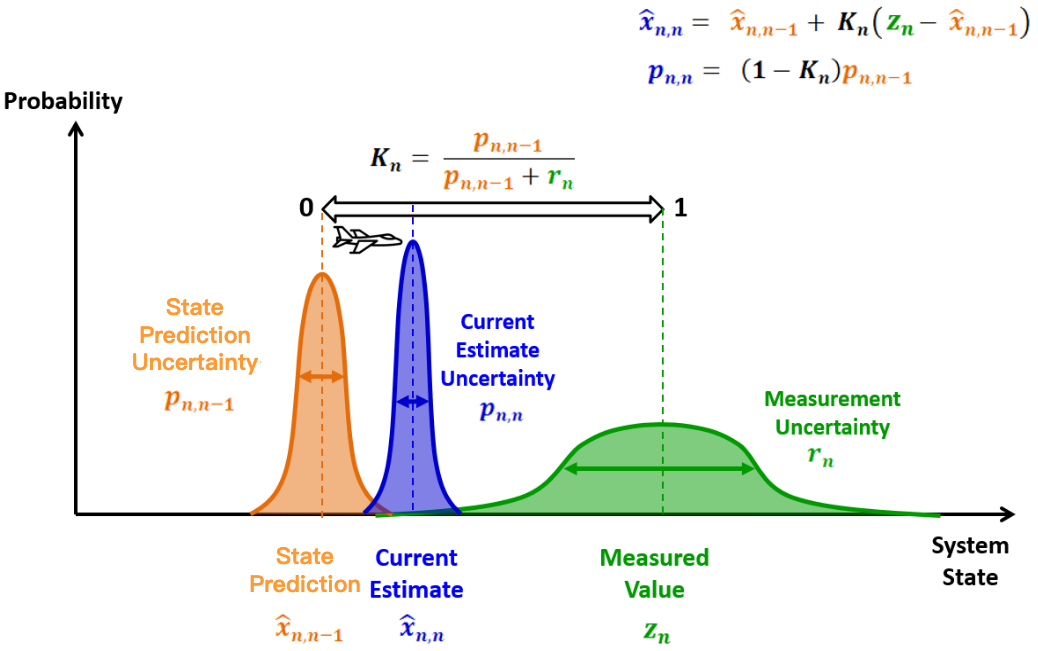
t r ( P _ n , n ) = t r ( P _ n , n β 1 ) β t r ( P _ n , n β 1 H T K _ n T ) β t r ( K _ n HP _ n , n β 1 ) + t r ( K _ n ( HP _ n , n β 1 H T + R _ n ) K _ n T ) β£ t r ( A ) = t r ( A T ) t r ( P _ n , n ) = t r ( P _ n , n β 1 ) β 2 t r ( K _ n HP _ n , n β 1 ) + t r ( K _ n ( HP _ n , n β 1 H T + R _ n ) K _ n T ) d K _ n d β t r ( P _ n , n ) = d K _ n d β t r ( P _ n , n β 1 ) β d K _ n d β 2 t r ( K _ n HP _ n , n β 1 ) + d K _ n d t r ( K _ n ( HP _ n , n β 1 H T + R _ n ) K _ n T ) β = ! 0 β£ d A d β t r ( AB ) = B T , d A d β t r ( AB A T ) = 2 AB d K _ n d ( t r ( P _ n , n ) ) β = 0 β 2 ( HP _ n , n β 1 ) T + 2 K _ n ( HP _ n , n β 1 H T + R _ n ) = 0 ( HP _ n , n β 1 ) T = K _ n ( HP _ n , n β 1 H T + R _ n ) K _ n = ( HP _ n , n β 1 ) T ( HP _ n , n β 1 H T + R _ n ) β 1 β£ ( AB ) T = B T A T K _ n = P _ n , n β 1 T H T ( HP _ n , n β 1 H T + R _ n ) β 1 β£ covariance matrix P symmetric ( P T = P ) K _ n = P _ n , n β 1 H T ( HP _ n , n β 1 H T + R _ n ) β 1 β Kalman Gain intuition The Kalman gain tells how much I should refine my prediction (i.e. , the a priori estimate) by given a measurement. We show the intuition of Kalman Gain with a one-dimensional Kalman filter.
The one-dimensional Kalman Gain is
K n = p n , n β 1 p n , n β 1 + r n β [ 0 , 1 ]
\boldsymbol{K}_{\boldsymbol{n}}=\frac{p_{n, n-1}}{p_{n, n-1}+r_{n}} \in [0, 1]
K n β = p n , n β 1 β + r n β p n , n β 1 β β β [ 0 , 1 ] p n , n β 1 p_{n, n-1} p n , n β 1 β x ^ n , n β 1 \hat{x}_{n, n-1} x ^ n , n β 1 β r n r_n r n β z n z_n z n β (Derivation see here )
Letβs rewrite the (one-dimensional) state update equation :
x ^ n , n = x ^ n , n β 1 + K n ( z n β x ^ n , n β 1 ) = ( 1 β K n ) x ^ n , n β 1 + K n z n
\hat{x}_{n, n}=\hat{x}_{n, n-1}+K_{n}\left(z_{n}-\hat{x}_{n, n-1}\right)=\left(1-K_{n}\right) \hat{x}_{n, n-1}+K_{n} z_{n}
x ^ n , n β = x ^ n , n β 1 β + K n β ( z n β β x ^ n , n β 1 β ) = ( 1 β K n β ) x ^ n , n β 1 β + K n β z n β The Kalman Gain K n K_n K n β weight that we give to the measurement. And ( 1 β K n ) (1 - K_n) ( 1 β K n β )
High Kalman Gain
A low measurement uncertainty (small r n r_n r n β
π‘ Intuition
small r n β r_n \rightarrow r n β β β \rightarrow β
Low Kalman Gain
A high measurement uncertainty (large r n r_n r n β
π‘ Intuition
large r n β r_n \rightarrow r n β β β \rightarrow β
State update equation The state update equation updates/refines/corrects the state prediction with measurements.
x ^ n , n = x ^ n , n β 1 + K n ( z n β H x ^ n , n β 1 ) β innovation
\hat{\boldsymbol{x}}_{\boldsymbol{n}, \boldsymbol{n}}=\hat{\boldsymbol{x}}_{\boldsymbol{n}, \boldsymbol{n}-1}+\mathbf{K}_{\boldsymbol{n}}\underbrace{\left(\boldsymbol{z}_{n}-\mathbf{H} \hat{\boldsymbol{x}}_{\boldsymbol{n}, \boldsymbol{n}-1}\right)}_{\text{innovation}}
x ^ n , n β = x ^ n , n β 1 β + K n β innovation ( z n β β H x ^ n , n β 1 β ) β β x ^ n , n \hat{\boldsymbol{x}}_{n, n} x ^ n , n β n n n
x ^ n , n β 1 \hat{\boldsymbol{x}}_{n, n-1} x ^ n , n β 1 β predicted system state vector at time step n n n
K n \mathbf{K}_{\boldsymbol{n}} K n β Kalman Gain
H \mathbf{H} H
z n \boldsymbol{z}_{n} z n β n n n
z n = H x n + v n
\boldsymbol{z}_{n} = \mathbf{H} \boldsymbol{x}_n + \boldsymbol{v}_n
z n β = H x n β + v n β x n \boldsymbol{x}_n x n β
v n \boldsymbol{v}_n v n β
β \rightarrow β R n \mathbf{R}_n R n β
R n = E { v n v n T }
\mathbf{R}_n = E\{\boldsymbol{v}_n \boldsymbol{v}_n^T\}
R n β = E { v n β v n T β } Covariance update equation The covariance update equation updates the uncertainty of state estimate on the base of covariance prediction
P n , n = ( I β K n H ) P n , n β 1 ( I β K n H ) T + K n R n K n T
\mathbf{P}_{n, n}=\left(\mathbf{I}-\mathbf{K}_{n} \mathbf{H}\right) \mathbf{P}_{n, n-1}\left(\mathbf{I}-\mathbf{K}_{n} \mathbf{H}\right)^{T}+\mathbf{K}_{n} \mathbf{R}_{n} \mathbf{K}_{n}^{T}
P n , n β = ( I β K n β H ) P n , n β 1 β ( I β K n β H ) T + K n β R n β K n T β Derivation According to state update equation :
x ^ _ n , n = x ^ _ n , n β 1 + K _ n ( z _ n β H x ^ _ n , n β 1 ) = x ^ _ n , n β 1 + K _ n ( H x _ n + v _ n β H x ^ _ n , n β 1 )
\begin{aligned}
\hat{\boldsymbol{x}}\_{n, n} &= \hat{\boldsymbol{x}}\_{n, n-1}+\mathbf{K}\_{n}\left(\boldsymbol{z}\_{n}-\mathbf{H} \hat{\boldsymbol{x}}\_{n, n-1}\right) \\\\\\\\
&= \hat{\boldsymbol{x}}\_{n, n-1}+\mathbf{K}\_{n}\left(\mathbf{H} \boldsymbol{x}\_n + \boldsymbol{v}\_n-\mathbf{H} \hat{\boldsymbol{x}}\_{n, n-1}\right)
\end{aligned}
x ^ _ n , n β = x ^ _ n , n β 1 + K _ n ( z _ n β H x ^ _ n , n β 1 ) = x ^ _ n , n β 1 + K _ n ( H x _ n + v _ n β H x ^ _ n , n β 1 ) β The estimation error between the true (hidden) state x _ n \boldsymbol{x}\_n x _ n x ^ _ n , n \hat{\boldsymbol{x}}\_{n, n} x ^ _ n , n
e _ n = x _ n β x ^ _ n , n = x _ n β x ^ _ n , n β 1 β K _ n H x _ n β K _ n v _ n + K _ n H x ^ _ n , n β 1 = x _ n β x ^ _ n , n β 1 β K _ n H ( x _ n β x ^ _ n , n β 1 ) β K _ n v _ n = ( I β K _ n H ) ( x _ n β x ^ _ n , n β 1 ) β K _ n v _ n
\begin{aligned}
\boldsymbol{e}\_n &= \boldsymbol{x}\_n - \hat{\boldsymbol{x}}\_{n, n} \\\\
&= \boldsymbol{x}\_n - \hat{\boldsymbol{x}}\_{n, n-1} - \mathbf{K}\_{n}\mathbf{H}\boldsymbol{x}\_n - \mathbf{K}\_{n}\boldsymbol{v}\_n + \mathbf{K}\_{n}\mathbf{H} \hat{\boldsymbol{x}}\_{n, n-1}\\\\
&= \boldsymbol{x}\_n - \hat{\boldsymbol{x}}\_{n, n-1} - \mathbf{K}\_{n}\mathbf{H}(\boldsymbol{x}\_n - \hat{\boldsymbol{x}}\_{n, n-1}) - \mathbf{K}\_{n}\boldsymbol{v}\_n \\\\
&= (\mathbf{I} - \mathbf{K}\_{n}\mathbf{H})(\boldsymbol{x}\_n - \hat{\boldsymbol{x}}\_{n, n-1}) - \mathbf{K}\_{n}\boldsymbol{v}\_n
\end{aligned}
e _ n β = x _ n β x ^ _ n , n = x _ n β x ^ _ n , n β 1 β K _ n H x _ n β K _ n v _ n + K _ n H x ^ _ n , n β 1 = x _ n β x ^ _ n , n β 1 β K _ n H ( x _ n β x ^ _ n , n β 1 ) β K _ n v _ n = ( I β K _ n H ) ( x _ n β x ^ _ n , n β 1 ) β K _ n v _ n β Estimate Uncertainty
P _ n , n = E ( e _ n e _ n T ) = E ( ( x _ n β x ^ _ n , n ) ( x _ n β x ^ _ n , n ) T ) β£ Plug in e _ n P _ n , n = E ( ( ( I β K _ n H ) ( x _ n β x ^ _ n , n β 1 ) β K _ n v _ n ) Γ ( ( I β K _ n H ) ( x _ n β x ^ _ n , n β 1 ) β K _ n v _ n ) T ) P _ n , n = E ( ( ( I β K _ n H ) ( x _ n β x ^ _ n , n β 1 ) β K _ n v _ n ) Γ ( ( ( I β K _ n H ) ( x _ n β x ^ _ n , n β 1 ) ) T β ( K _ n v _ n ) T ) ) β£ ( A B ) T = B T A T P _ n , n = E ( ( ( I β K _ n H ) ( x _ n β x ^ _ n , n β 1 ) β K _ n v _ n ) Γ ( ( x _ n β x ^ _ n , n β 1 ) T ( I β K _ n H ) T β ( K _ n v _ n ) T ) ) P _ n , n = E ( ( I β K _ n H ) ( x _ n β x ^ _ n , n β 1 ) ( x _ n β x ^ _ n , n β 1 ) T ( I β K _ n H ) T β ( I β K _ n H ) ( x _ n β x ^ _ n , n β 1 ) ( K _ n v _ n ) T β K _ n v _ n ( x _ n β x ^ _ n , n β 1 ) T ( I β K _ n H ) T + K _ n v _ n ( K _ n v _ n ) T ) β£ E ( X Β± Y ) = E ( X ) Β± E ( Y ) P _ n , n = E ( ( I β K _ n H ) ( x _ n β x ^ _ n , n β 1 ) ( x _ n β x ^ _ n , n β 1 ) T ( I β K _ n H ) T ) β E ( ( I β K _ n H ) ( x _ n β x ^ _ n , n β 1 ) ( K _ n v _ n ) T ) β E ( K _ n v _ n ( x _ n β x ^ _ n , n β 1 ) T ( I β K _ n H ) T ) + E ( K _ n v _ n ( K _ n v _ n ) T )
\begin{array}{l}
\boldsymbol{\mathbf{P}}\_{n, n}=E\left(\boldsymbol{e}\_{n} \boldsymbol{e}\_{n}^{T}\right)=E\left(\left(\boldsymbol{x}\_{n}-\hat{\boldsymbol{x}}\_{n, n}\right)\left(\boldsymbol{x}\_{n}-\hat{\boldsymbol{x}}\_{n, n}\right)^{T}\right) \qquad | \text{ Plug in } \boldsymbol{e}\_n\\\\\\\\
\boldsymbol{\mathbf{P}}\_{n, n}=E\left(\left(\left(\mathbf{I}-\mathbf{K}\_{n} \mathbf{H}\right)\left(\boldsymbol{x}\_{n}-\hat{x}\_{n, n-1}\right)-\mathbf{K}\_{n} v\_{n}\right) \right.\\\\
\left.\times\left(\left(\mathbf{I}-\mathbf{K}\_{n} \mathbf{H}\right)\left(\boldsymbol{x}\_{n}-\hat{x}\_{n, n-1}\right)-\mathbf{K}\_{n} v\_{n}\right)^{T}\right)\\\\\\\\
\mathbf{P}\_{n, n}=E\left(\left(\left(\mathbf{I}-\boldsymbol{\mathbf{K}}\_{n} \mathbf{H}\right)\left(\boldsymbol{x}\_{n}-\hat{\boldsymbol{x}}\_{n, n-1}\right)-\boldsymbol{\mathbf{K}}\_{n} v\_{n}\right) \right.\\\\
\left.\times\left(\left(\left(\mathbf{I}-\mathbf{K}\_{n} \mathbf{H}\right)\left(\boldsymbol{x}\_{n}-\hat{x}\_{n, n-1}\right)\right)^{T}-\left(\mathbf{K}\_{n} v\_{n}\right)^{T}\right)\right) \qquad | \text{ }(\mathbf{A} \mathbf{B})^{T}=\mathbf{B}^{T} \mathbf{A}^{T} \\\\\\\\
\mathbf{P}\_{n, n}=E\left(\left(\left(\mathbf{I}-\mathbf{K}\_{n} \mathbf{H}\right)\left(\boldsymbol{x}\_{n}-\hat{x}\_{n, n-1}\right)-\mathbf{K}\_{n} v\_{n}\right) \right. \\\\
\left.\times\left(\left(\boldsymbol{x}\_{n}-\hat{x}\_{n, n-1}\right)^{T}\left(\mathbf{I}-\mathbf{K}\_{n} \mathbf{H}\right)^{T}-\left(\mathbf{K}\_{n} v\_{n}\right)^{T}\right)\right)\\\\\\\\
\mathbf{P}\_{n, n}=E\left(\left(\mathbf{I}-\mathbf{K}\_{n} \mathbf{H}\right)\left(\boldsymbol{x}\_{n}-\hat{x}\_{n, n-1}\right)\left(\boldsymbol{x}\_{n}-\hat{\boldsymbol{x}}\_{n, n-1}\right)^{T}\left(\mathbf{I}-\mathbf{K}\_{n} \mathbf{H}\right)^{T}\right.\\\\
-\left(\mathbf{I}-\mathbf{K}\_{n} \mathbf{H}\right)\left(\boldsymbol{x}\_{n}-\hat{x}\_{n, n-1}\right)\left(\mathbf{K}\_{n} v\_{n}\right)^{T}\\\\
-\mathbf{K}\_{n} v\_{n}\left(\boldsymbol{x}\_{n}-\hat{x}\_{n, n-1}\right)^{T}\left(\mathbf{I}-\mathbf{K}\_{n} \mathbf{H}\right)^{T}\\\\
\left.+\mathbf{K}\_{n} v\_{n}\left(\mathbf{K}\_{n} v\_{n}\right)^{T}\right) \qquad | \text{ } E(X \pm Y)=E(X) \pm E(Y)\\\\\\\\
\mathbf{P}\_{n, n}=E\left(\left(\mathbf{I}-\mathbf{K}\_{n} \mathbf{H}\right)\left(\boldsymbol{x}\_{n}-\hat{x}\_{n, n-1}\right)\left(\boldsymbol{x}\_{n}-\hat{x}\_{n, n-1}\right)^{T}\left(\mathbf{I}-\mathbf{K}\_{n} \mathbf{H}\right)^{T}\right)\\\\
-\color{red}{E\left(\left(\mathbf{I}-\mathbf{K}\_{n} \mathbf{H}\right)\left(\boldsymbol{x}\_{n}-\hat{x}\_{n, n-1}\right)\left(\mathbf{K}\_{n} v\_{n}\right)^{T}\right)}\\\\
-\color{red}{E\left(\mathbf{K}\_{n} v\_{n}\left(\boldsymbol{x}\_{n}-\hat{x}\_{n, n-1}\right)^{T}\left(\mathbf{I}-\mathbf{K}\_{n} \mathbf{H}\right)^{T}\right)}\\\\
+E\left(\mathbf{K}\_{n} v\_{n}\left(\mathbf{K}\_{n} v\_{n}\right)^{T}\right)
\end{array}
P _ n , n = E ( e _ n e _ n T ) = E ( ( x _ n β x ^ _ n , n ) ( x _ n β x ^ _ n , n ) T ) β£ Plug in e _ n P _ n , n = E ( ( ( I β K _ n H ) ( x _ n β x ^ _ n , n β 1 ) β K _ n v _ n ) Γ ( ( I β K _ n H ) ( x _ n β x ^ _ n , n β 1 ) β K _ n v _ n ) T ) P _ n , n = E ( ( ( I β K _ n H ) ( x _ n β x ^ _ n , n β 1 ) β K _ n v _ n ) Γ ( ( ( I β K _ n H ) ( x _ n β x ^ _ n , n β 1 ) ) T β ( K _ n v _ n ) T ) ) β£ ( AB ) T = B T A T P _ n , n = E ( ( ( I β K _ n H ) ( x _ n β x ^ _ n , n β 1 ) β K _ n v _ n ) Γ ( ( x _ n β x ^ _ n , n β 1 ) T ( I β K _ n H ) T β ( K _ n v _ n ) T ) ) P _ n , n = E ( ( I β K _ n H ) ( x _ n β x ^ _ n , n β 1 ) ( x _ n β x ^ _ n , n β 1 ) T ( I β K _ n H ) T β ( I β K _ n H ) ( x _ n β x ^ _ n , n β 1 ) ( K _ n v _ n ) T β K _ n v _ n ( x _ n β x ^ _ n , n β 1 ) T ( I β K _ n H ) T + K _ n v _ n ( K _ n v _ n ) T ) β£ E ( X Β± Y ) = E ( X ) Β± E ( Y ) P _ n , n = E ( ( I β K _ n H ) ( x _ n β x ^ _ n , n β 1 ) ( x _ n β x ^ _ n , n β 1 ) T ( I β K _ n H ) T ) β E ( ( I β K _ n H ) ( x _ n β x ^ _ n , n β 1 ) ( K _ n v _ n ) T ) β E ( K _ n v _ n ( x _ n β x ^ _ n , n β 1 ) T ( I β K _ n H ) T ) + E ( K _ n v _ n ( K _ n v _ n ) T ) β x _ n β x ^ _ n , n β 1 \boldsymbol{x}\_{n}-\hat{x}\_{n, n-1} x _ n β x ^ _ n , n β 1 v _ n \boldsymbol{v}\_n v _ n
E ( ( I β K _ n H ) ( x _ n β x ^ _ n , n β 1 ) ( K _ n v _ n ) T ) = 0 E ( K _ n v _ n ( x _ n β x ^ _ n , n β 1 ) T ( I β K _ n H ) T ) = 0
\begin{aligned}
\color{red}{E\left(\left(\mathbf{I}-\mathbf{K}\_{n} \mathbf{H}\right)\left(\boldsymbol{x}\_{n}-\hat{x}\_{n, n-1}\right)\left(\mathbf{K}\_{n} v\_{n}\right)^{T}\right)} = 0 \\\\
\color{red}{E\left(\mathbf{K}\_{n} v\_{n}\left(\boldsymbol{x}\_{n}-\hat{x}\_{n, n-1}\right)^{T}\left(\mathbf{I}-\mathbf{K}\_{n} \mathbf{H}\right)^{T}\right)} = 0
\end{aligned}
E ( ( I β K _ n H ) ( x _ n β x ^ _ n , n β 1 ) ( K _ n v _ n ) T ) = 0 E ( K _ n v _ n ( x _ n β x ^ _ n , n β 1 ) T ( I β K _ n H ) T ) = 0 β Therefore
P _ n , n = E ( ( I β K _ n H ) ( x _ n β x ^ _ n , n β 1 ) ( x _ n β x ^ _ n , n β 1 ) T ( I β K _ n H ) T ) + E ( K _ n v _ n ( K _ n v _ n ) T ) β£ ( A B ) T = B T A T P _ n , n = E ( ( I β K _ n H ) ( x _ n β x ^ _ n , n β 1 ) ( x _ n β x ^ _ n , n β 1 ) T ( I β K _ n H ) T ) + E ( K _ n v _ n v _ n T K _ n T ) β£ E ( a X ) = a E ( X ) P _ n , n = ( I β K _ n H ) E ( ( x _ n β x ^ _ n , n β 1 ) ( x _ n β x ^ _ n , n β 1 ) T ) β _ = P _ n , n β 1 ( I β K _ n H ) T + K _ n E ( v _ n v _ n T ) β _ = R _ n K _ n T P _ n , n = ( I β K _ n H ) P _ n , n β 1 ( I β K _ n H ) T + K _ n R _ n K _ n T
\begin{array}{l}
\mathbf{P}\_{n, n}=E\left(\left(\mathbf{I}-\mathbf{K}\_{n} \mathbf{H}\right)\left(\boldsymbol{x}\_{n}-\hat{x}\_{n, n-1}\right)\left(\boldsymbol{x}\_{n}-\hat{x}\_{n, n-1}\right)^{T}\left(\mathbf{I}-\mathbf{K}\_{n} \mathbf{H}\right)^{T}\right)\\\\
+{\color{DodgerBlue}{E\left(\mathbf{K}\_{n} v\_{n}\left(\mathbf{K}\_{n} v\_{n}\right)^{T}\right)}} \qquad | \text{ }(\mathbf{A} \mathbf{B})^{T}=\mathbf{B}^{T} \mathbf{A}^{T} \\\\\\\\
\mathbf{P}\_{n, n}=E\left(\left(\mathbf{I}-\mathbf{K}\_{n} \mathbf{H}\right)\left(\boldsymbol{x}\_{n}-\hat{x}\_{n, n-1}\right)\left(\boldsymbol{x}\_{n}-\hat{x}\_{n, n-1}\right)^{T}\left(\mathbf{I}-\mathbf{K}\_{n} \mathbf{H}\right)^{T}\right)\\\\
+{\color{DodgerBlue}{E\left(\mathbf{K}\_{n} v\_{n} v\_{n}^T \mathbf{K}\_{n}^T\right)}} \qquad | \text{ } E(a X)=a E(X) \\\\\\\\
\mathbf{P}\_{n, n} = \left(\mathbf{I}-\mathbf{K}\_{n} \mathbf{H}\right) {\color{ForestGreen}\underbrace{{E\left(\left(\boldsymbol{x}\_{n}-\hat{x}\_{n, n-1}\right)\left(\boldsymbol{x}\_{n}-\hat{x}\_{n, n-1}\right)^{T}\right)}}\_{=\mathbf{P}\_{n, n-1}}}\left(\mathbf{I}-\mathbf{K}\_{n} \mathbf{H}\right)^{T}
+\mathbf{K}\_{n}{\color{DodgerBlue}{\underbrace{E\left( v\_{n} v\_{n}^T \right)}\_{=\mathbf{R}\_n}}} \mathbf{K}\_{n}^T \\\\\\\\
\mathbf{P}\_{n, n} = \left(\mathbf{I}-\mathbf{K}\_{n} \mathbf{H}\right) {\color{ForestGreen}\mathbf{P}\_{n, n-1}} \left(\mathbf{I}-\mathbf{K}\_{n} \mathbf{H}\right)^{T} +\mathbf{K}\_{n}{\color{DodgerBlue}\mathbf{R}\_n} \mathbf{K}\_{n}^T
\end{array}
P _ n , n = E ( ( I β K _ n H ) ( x _ n β x ^ _ n , n β 1 ) ( x _ n β x ^ _ n , n β 1 ) T ( I β K _ n H ) T ) + E ( K _ n v _ n ( K _ n v _ n ) T ) β£ ( AB ) T = B T A T P _ n , n = E ( ( I β K _ n H ) ( x _ n β x ^ _ n , n β 1 ) ( x _ n β x ^ _ n , n β 1 ) T ( I β K _ n H ) T ) + E ( K _ n v _ n v _ n T K _ n T ) β£ E ( a X ) = a E ( X ) P _ n , n = ( I β K _ n H ) E ( ( x _ n β x ^ _ n , n β 1 ) ( x _ n β x ^ _ n , n β 1 ) T ) β _ = P _ n , n β 1 ( I β K _ n H ) T + K _ n E ( v _ n v _ n T ) β _ = R _ n K _ n T P _ n , n = ( I β K _ n H ) P _ n , n β 1 ( I β K _ n H ) T + K _ n R _ n K _ n T β In many textbook you can see a simplified form:
P n , n = ( I β K n H ) P n , n β 1
\mathbf{P}_{n, n}=\left(\mathbf{I}-\mathbf{K}_{n} \mathbf{H}\right) \mathbf{P}_{n, n-1}
P n , n β = ( I β K n β H ) P n , n β 1 β This equation is elegant and easier to remember and in many cases it performs well.
However, even the smallest error in computing the Kalman Gain (due to round off) can lead to huge computation errors. The subtraction ( I β K n H ) \left(\mathbf{I}-\mathbf{K}_{n} \mathbf{H}\right) ( I β K n β H ) numerically unstable !
Derivation of a simplified form of the Covariance Update Equation P _ n , n = ( I β K _ n H ) P _ n , n β 1 ( I β K _ n H ) T + K _ n R _ n K _ n T P _ n , n = P _ n , n β 1 β P _ n , n β 1 H T K _ n T β K _ n H P _ n , n β 1 + K _ n ( H P _ n , n β 1 H T + R _ n ) K _ n T β£ Substitute Kalman Gain P _ n , n = P _ n , n β 1 β P _ n , n β 1 H T K _ n T β K _ n H P _ n , n β 1 + P _ n , n β 1 H T ( H P _ n , n β 1 H T + R _ n ) β 1 ( H P _ n , n β 1 H T + R _ n ) β _ = 1 K _ n T P _ n , n = P _ n , n β 1 β P _ n , n β 1 H T K _ n T β K _ n H P _ n , n β 1 + P _ n , n β 1 H T K _ n T P _ n , n = P _ n , n β 1 β K _ n H P _ n , n β 1 P _ n , n = ( I β K _ n H ) P _ n , n β 1
\begin{array}{l}
\mathbf{P}\_{n, n} = \left(\mathbf{I}-\mathbf{K}\_{n} \mathbf{H}\right) \mathbf{P}\_{n, n-1} \left(\mathbf{I}-\mathbf{K}\_{n} \mathbf{H}\right)^{T} +\mathbf{K}\_{n}\mathbf{R}\_n \mathbf{K}\_{n}^T \\\\\\\\
\mathbf{P}\_{n, n}=\mathbf{P}\_{n, n-1}-\mathbf{P}\_{n, n-1} \boldsymbol{\mathbf{H}}^{T} \mathbf{K}\_{n}^{T}-\boldsymbol{\mathbf{K}}\_{n} \mathbf{H} \mathbf{P}\_{n, n-1} \\\\
+{\color{MediumOrchid}\mathbf{K}\_{n}}\left(\mathbf{H} \mathbf{P}\_{n, n-1} \mathbf{H}^{T}+\mathbf{R}\_{n}\right) \mathbf{K}\_{n}^{T} \qquad | \text{ Substitute Kalman Gain}\\\\\\\\
\mathbf{P}\_{n, n}=\mathbf{P}\_{n, n-1}-\mathbf{P}\_{n, n-1} \mathbf{H}^{T} \mathbf{K}\_{n}^{T}-\mathbf{K}\_{n} \mathbf{H} \mathbf{P}\_{n, n-1} \\\\
+{\color{MediumOrchid}\mathbf{P}\_{n, n-1}} \underbrace{{\color{MediumOrchid}{\mathbf{H}^{T}\left(\mathbf{H} \mathbf{P}\_{n, n-1} \mathbf{H}^{T}+\mathbf{R}\_{n}\right)^{-1}}}\left(\mathbf{H} \mathbf{P}\_{n, n-1} \mathbf{H}^{T}+\mathbf{R}\_{n}\right)}\_{=1} \mathbf{K}\_{n}^{T} \\\\\\\\
\mathbf{P}\_{n, n}=\mathbf{P}\_{n, n-1}-\mathbf{P}\_{n, n-1} \mathbf{H}^{T} \mathbf{K}\_{n}^{T}-\mathbf{K}\_{n} \mathbf{H} \mathbf{P}\_{n, n-1} \\\\
+\mathbf{P}\_{n, n-1} \mathbf{H}^{T} \mathbf{K}\_{n}^{T} \\\\\\\\
\mathbf{P}\_{n, n}=\mathbf{P}\_{n, n-1}-\mathbf{K}\_{n} \mathbf{H} \mathbf{P}\_{n, n-1} \\\\\\\\
\mathbf{P}\_{n, n}=\left(\mathbf{I}-\mathbf{K}\_{n} \mathbf{H}\right) \mathbf{P}\_{n, n-1}
\end{array}
P _ n , n = ( I β K _ n H ) P _ n , n β 1 ( I β K _ n H ) T + K _ n R _ n K _ n T P _ n , n = P _ n , n β 1 β P _ n , n β 1 H T K _ n T β K _ n HP _ n , n β 1 + K _ n ( HP _ n , n β 1 H T + R _ n ) K _ n T β£ Substitute Kalman Gain P _ n , n = P _ n , n β 1 β P _ n , n β 1 H T K _ n T β K _ n HP _ n , n β 1 + P _ n , n β 1 H T ( HP _ n , n β 1 H T + R _ n ) β 1 ( HP _ n , n β 1 H T + R _ n ) β _ = 1 K _ n T P _ n , n = P _ n , n β 1 β P _ n , n β 1 H T K _ n T β K _ n HP _ n , n β 1 + P _ n , n β 1 H T K _ n T P _ n , n = P _ n , n β 1 β K _ n HP _ n , n β 1 P _ n , n = ( I β K _ n H ) P _ n , n β 1 β Reference 
