Docs
Notes
SI
Wertdiskrete Systeme
Zustandsschätzung

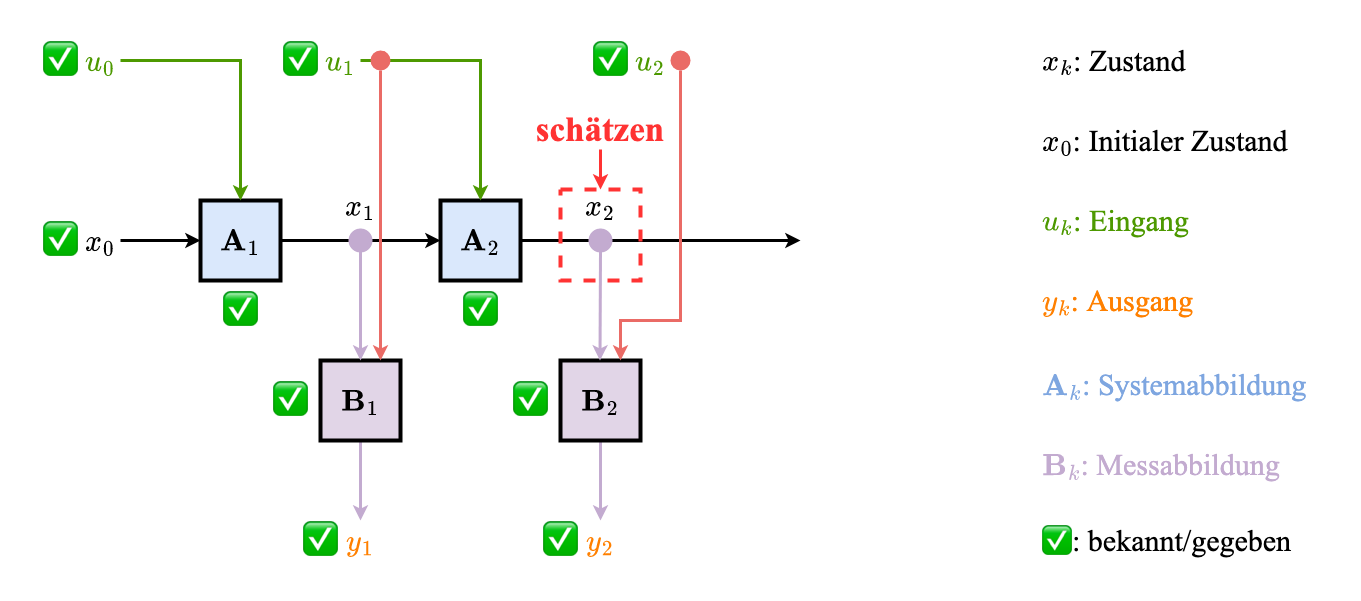
Zustandsschätzung

Vorbemerkungen

Bayessches Gesetz und erweiterte Konditionierung

P(a∣b)⋅P(b)=P(a,b)=P(b∣a)⋅P(a)⇒P(b∣a)=P(a∣b)⋅P(b)P(a) \begin{array}{l} &P(a \mid b) \cdot P(b)=P(a, b)=P(b \mid a) \cdot P(a) \\\\ \Rightarrow &P(b \mid a)=\frac{P(a | b) \cdot P(b)}{P(a)} \end{array}

Erweiterte Konditionierung:

P(b∣a,c)⋅P(a,c)⏟P(a∣c)⋅P(c)=P(a,b,c)=P(a∣b,c)⋅P(b,c)⏟P(b∣c)⋅P(c)⇒P(b∣a,c)⋅P(a∣c)=P(a∣b,c)⋅P(b∣c)(△)⇒P(b∣a,c)=P(a∣b,c)⋅P(b∣c)P(a∣c) \begin{array}{l} P(b \mid a, c) \cdot \underbrace{P(a, c)}_{P(a \mid c) \cdot P(c)}=P(a, b, c)=P(a \mid b, c) \cdot \underbrace{P(b, c)}_{P(b \mid c) \cdot P(c)} \\\\ \Rightarrow P(b \mid a, c) \cdot P(a \mid c)=P(a \mid b, c) \cdot P(b \mid c) \quad (\triangle) \\\\ \Rightarrow P(b \mid a, c)=\frac{P(a \mid b, c) \cdot P(b \mid c)}{P(a \mid c)} \end{array}

Notation zu Abhängigkeit vom Eingang

Abhängigkeit der Systemmatrizen Ak\mathbf{A}_k (Übergangsmatrix) und Bk\mathbf{B}_k (Messe-/Beobachtungsmatrix) von Eingang uku_k (4 dimensionale Felde):

wertdiskrete_systeme-abhaengigkeit_von_Eingang

Schreibweise:

A(k,uk,Xk+1=xk+1,Xk=xk)=A(k,uk,xk+1,xk)=Ak(uk,xk+1,xk)=Akuk(xk+1,xk) \begin{array}{l} &A\left(k, u_{k}, X_{k+1} = x_{k+1}, X_{k}=x_{k}\right) \\ = &A\left(k, u_{k}, x_{k+1}, x_{k}\right) \\ = &A_{k}\left(u_{k}, x_{k+1}, x_{k}\right) \\ = &A_{k}^{u_{k}}\left(x_{k+1}, x_{k}\right) \\ \end{array}

“Zum Zeitpunkt kk ist der aktuelle Zustand Xk=xkX_k=x_k. Was ist die Wahrscheinlichkeit vom den nächsten Zustand Xk+1=xk+1X_{k+1}=x_{k+1}, wenn der Eingang uku_k ist?”

Zeitinvariante Fall:

A(uk,xk+1,xk)=Auk(xk+1,xk) A(u_k, x_{k+1}, x_k) = A_{u_k}(x_{k+1}, x_k)

Zustandsschätzung

Ziel

Rekonstruktion des internen Zustands aus Messungen und Eingängen (Annahme: Ak,Bk\mathbf{A}_k, \mathbf{B}_k bekannt)

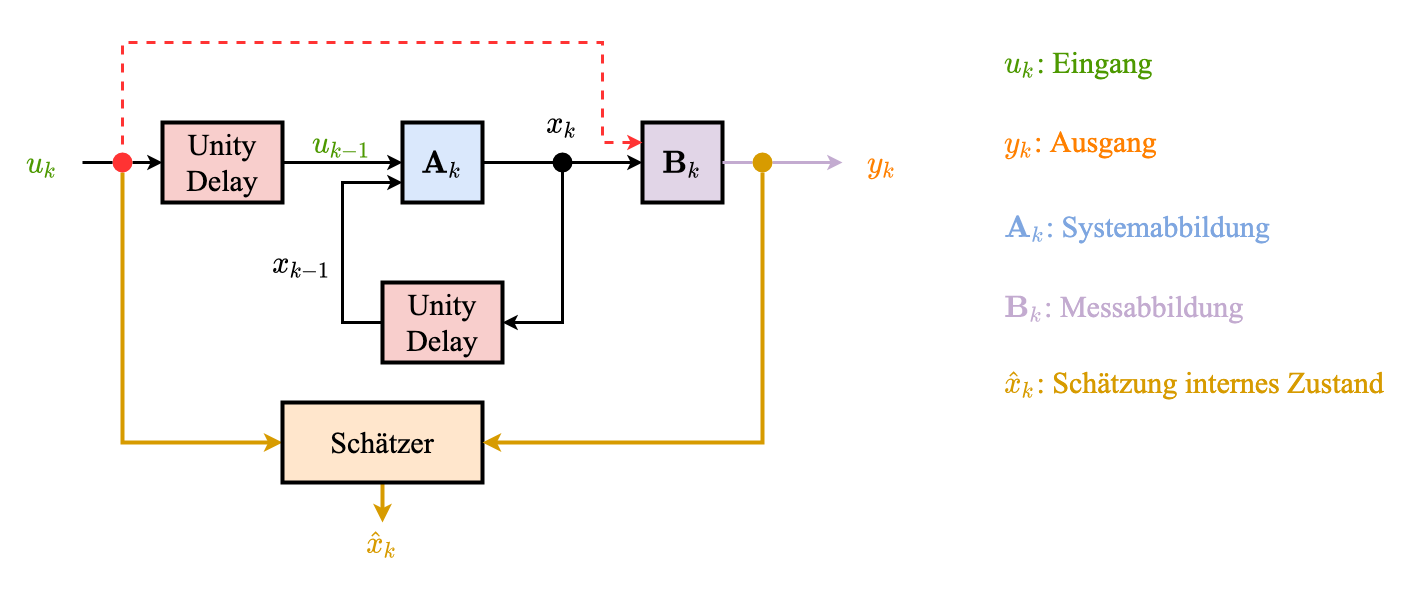
Interner Zustand Schätzer

Interner Zustand Schätzer

Problemformulierung

  • Gegeben

    • Eingänge uk,k=0,…,kuu_k, k = 0, \dots, k_u

    • Messungen yk,k=1,…,kyy_k, k = 1, \dots, k_y

  • Gesucht: Rekonstruktion des Zustands

    • x^k,k=1,…,kx\hat{x}_k, k = 1, \dots, k_x (alle interne Zustände)

    • x^kx\hat{x}_{k_x} (der letzte Zustand)

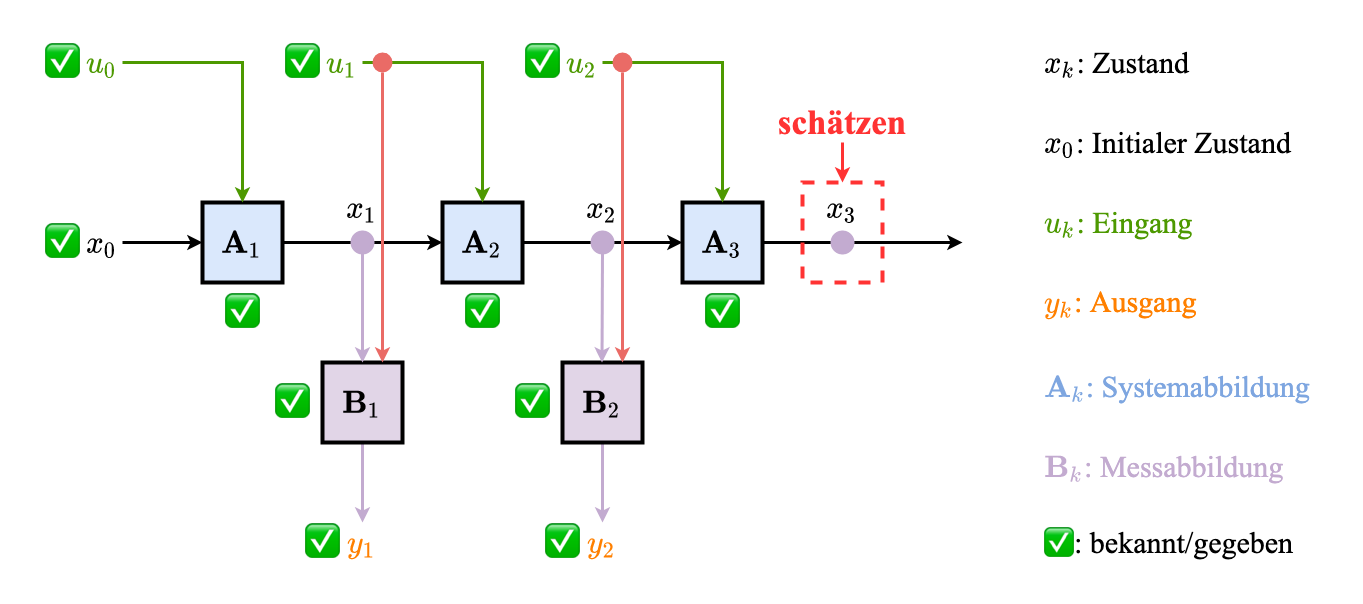
  • Bsp Darstellung

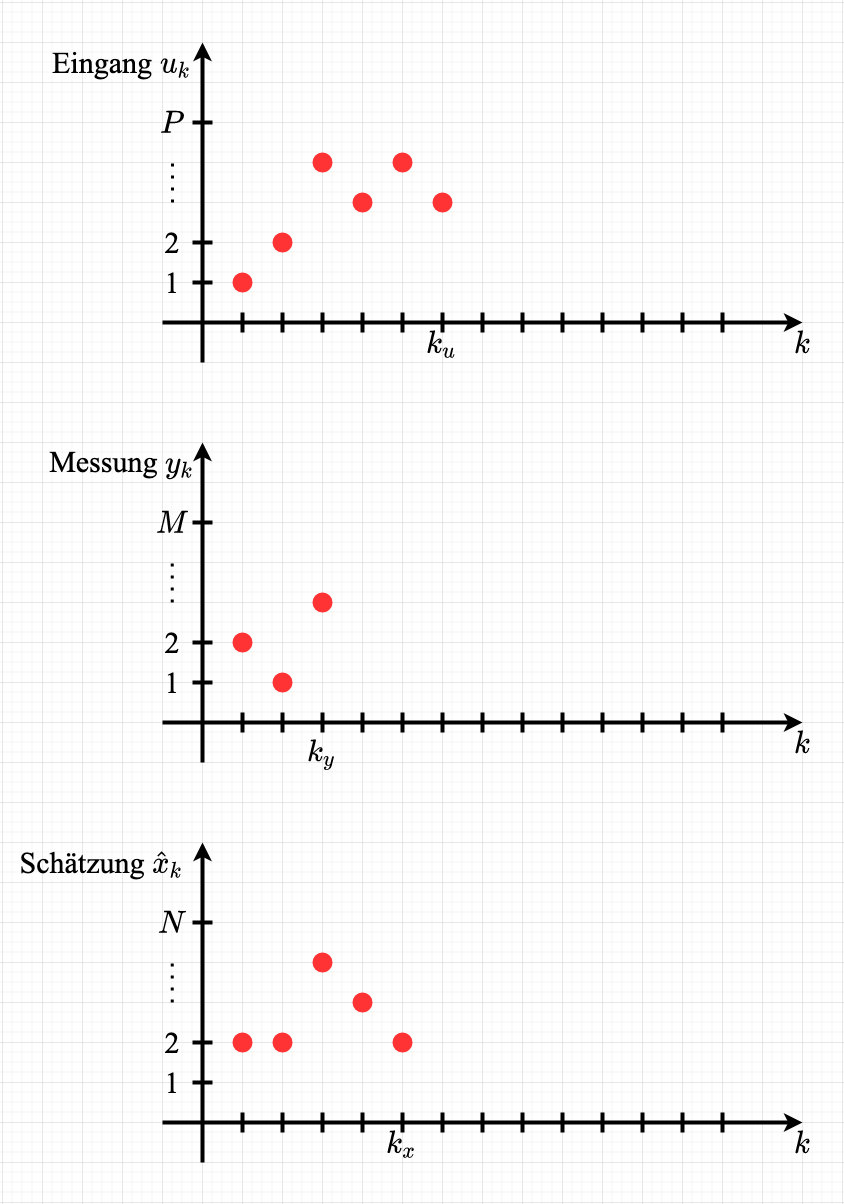
    wertdiskrete_systeme-Schaetzung_Problemformulierung_grid

  • Paradigma: Nutzung aller Daten

  • Zwei wichtige Fälle/Phasen

    • Prädiktion (ku+1=kx>kyk_u + 1 = k_x > k_y)

      Eine Prädiktion für den aktuellen Zustand basierend auf den letzten Zustand machen

    • Filterung (ku+1=kx=kyk_u + 1 = k_x = k_y)

      Mit der beobachtbaren Messungen die Prädiktion updaten/verfeinern

Prädiktion

Allgemein

  • Gegeben

    • Schätzung des Zustands zu einem Zeitpunkt mm, welche gesamte Eingang- und Messhistorik bis dahin enthält

    • Eingänge uku_k für k>mk > m

    • Systemmatrizen AkA_k für k>mk>m

  • Interpretation

    Ab Zeitpunkt m+1m+1 fehlen Messungen. Wie entwicklt sich System rein auf Basis des Systemmodells?

  • Gesucht

    Prädiktion zu späteren Zeitpunkt k>mk>m für gegeben Eingänge bis k−1k-1

    P(xk∣y1:m,u0:k−1) P(x_k \mid y_{1:m}, u_{0: k- 1})

    für xk∈{1,…,N}x_k \in \{1, \dots, N\}

Beispiel:

  • m=2,k=3m = 2, k =3

  • Prädiktion:

    P(x3∣y1:2,u0:2) P(x_3 \mid y_{1:2}, u_{0:2})
wertdiskrete_systeme-Praediktion.drawio

Es ist wichtig, dem Bayessches Gesetz mit der erweiterten Konditionierung zu verwenden

P(a,b∣c)=P(a∣b,c)⋅P(b∣c)(∗) P(a, b \mid c) = P(a \mid b, c) \cdot P(b \mid c) \qquad (\ast)

Zum Zeitpunkt k>mk > m:

P(xk∣y0:m,u0:k−1)=P(xk∣y0,y1,⋯ ,ym,u0,u1,⋯uk−1)∣Marginalisierung=∑xk−1=1NP(xk,xk−1∣y0:m,u0:k−1)=(∗)∑xk−1=1NP(xk∣xk−1,y0:m,u0:k−1)P(xk−1∣y0:m,u0:k−1)∣Markov=∑xk−1=1NP(xk∣xk−1,uk−1)⏟U¨bergangswachrshheinlicheit ⋅P(xk−1∣y0:m,u0:k−2)⏟Scha¨tzung fu¨r k−1 (Rekursiv nach vorne)  \begin{array}{l} &P\left(x_{k} \mid y_{0: m}, u_{0: k-1}\right)\\ =&P\left(x_{k} \mid y_{0}, y_{1}, \cdots, y_{m}, u_{0}, u_{1}, \cdots u_{k-1}\right) \quad \mid \text{Marginalisierung}\\ =& \displaystyle \sum_{x_{k-1}=1}^{N} P\left(x_{k}, x_{k-1} \mid y_{0: m}, u_{0: k-1}\right)\\ \overset{(\ast)}{=}&\displaystyle \sum_{x_{k-1}=1}^{N} P\left(x_{k} \mid x_{k-1}, y_{0: m}, u_{0: k-1}\right) P\left(x_{k-1} \mid y_{0: m}, u_{0: k-1}\right) \quad \mid \text{Markov}\\ =&\displaystyle \sum_{x_{k-1}=1}^{N} \underbrace{P\left(x_{k} \mid x_{k-1}, u_{k-1}\right)}_{\text {Übergangswachrshheinlicheit }} \cdot \underbrace{P\left(x_{k-1} \mid y_{0: m}, u_{0 : k-2}\right)}_{\text {Schätzung für } k-1} \quad \text { (Rekursiv nach vorne) } \end{array}

(Die Summe beschreibt eine Vektor-Matrix-Multiplikation.)

Anordnen der Einzelwahrscheinlichkeit in Vektoren:

ηk∣1:mx=(P(xk=1∣y1:m,u0:k−1)⋮P(xk=N∣y1:m,u0:k−1))ηk−1∣1:mx=(P(xk−1=1∣y1:m,u0:k−2)⋮P(xk−1=N∣y1:m,u0:k−2)) \eta_{k \mid 1: m}^{x} = \left(\begin{array}{c} P\left(x_{k}=1 \mid y_{1: m}, u_{0: k-1}\right) \\ \vdots \\ P\left(x_{k}=N \mid y_{1: m}, u_{0: k-1}\right) \end{array}\right) \qquad \eta_{k-1 \mid 1: m}^{x}=\left(\begin{array}{c} P\left(x_{k-1}=1 \mid y_{1: m}, u_{0: k-2}\right) \\ \vdots \\ P\left(x_{k-1}=N \mid y_{1: m}, u_{0: k-2}\right) \end{array}\right)

Rekursive Prädiktion:

  • Beginn: Schätzvektor ηm∣1:mx\eta_{m \mid 1: m}^{x}

  • Rekursion: für k>mk > m

    ηk∣1:mx=Ak⊤ηk−1∣1:mx \eta_{k \mid 1: m}^{x}=\mathbf{A}_{k}^{\top} \eta_{k-1 \mid 1 : m}^{x}

  • Spezialfall: Einschrittprädiktion (k=m+1k = m + 1)

Konkretes Beispiel

  • Systemmodell (zeitinvariant)

    • Systemabbildung

      Auk=(a1(uk)1−a1(uk)a2(uk)1−a2(uk))a1(uk),a2(uk)∈[0,1] \mathbf{A}_{u_{k}}=\left(\begin{array}{ll} a_{1}\left(u_{k}\right) & 1-a_{1}\left(u_{k}\right) \\ a_{2}\left(u_{k}\right) & 1-a_{2}\left(u_{k}\right) \end{array}\right) \qquad a_{1}\left(u_{k}\right), a_{2}\left(u_{k}\right) \in[0,1]

      Reminder: A(i,j):=P(xk+1=j∣xk=i)A(i, j):=P\left(x_{k+1}=j \mid x_{k}=i\right)

    • Messeabbildung

      B=(b11−b1b21−b2)b1,b2∈[0,1] \mathbf{B}=\left(\begin{array}{ll} b_{1} & 1-b_{1} \\ b_{2} & 1-b_{2} \end{array}\right) \qquad b_1, b_2 \in [0, 1]

      Reminder: B(i,j):=P(yk=j∣xk=i)B(i, j):=P\left(y_{k}=j \mid x_{k}=i\right)

​

  • Gegeben

    • Initialer Zustandsschätzvektor

      η0x=[p01−p0](=P(x0))p0∈[0,1] \eta_{0}^{x}=\left[\begin{array}{c} p_{0} \\ 1-p_{0} \end{array}\right] (=P(x_0)) \qquad p_{0} \in[0,1]

      (Also: P(x0=1)=P0,P(x0=2)=1−P0P(x_0 = 1) = P_0, P(x_0 = 2) = 1- P_0)

      • Werte der Eingänge u0,u1,u2u_0, u_1, u_2

      • Keine Messungen

  • Gesucht

    • Verbundverteilung für die Zeitpunkt k=1,2,3k = 1, 2, 3

      P(x1,x2,x3∣u0,u1,u2)=:P(x1,3∣u0:2) P\left(x_{1}, x_{2}, x_{3} \mid u_{0}, u_{1}, u_{2}\right)=: P\left(x_{1,3} \mid u_{0: 2}\right)

    • Verteilung zum Zeitpunkt k=3k=3

      p(x3∣u0,u1,u2)=p(x3∣u0:2)=η3x(x3) p\left(x_{3} \mid u_{0}, u_{1}, u_{2}\right)=p\left(x_{3} \mid u_{0: 2}\right)=\eta_{3}^{x}\left(x_{3}\right)

    Also wir sind in Zeitschritt 0, und möchte Prädiktion machen für

    • zukünftige Zustände xk,k=1,2,3x_k, k = 1, 2, 3
    • zukünftige Messungen yk,k=1,2,3y_k, k=1,2,3

Aufspaltung der Verbundverteilung für k=0,1,2,3k = 0, 1, 2, 3:

P(x0:3∣u0:2)=(∗)P(x3∣x0:2,u0:2)⋅P(x0:2∣u0:2)=MarkovP(x3∣x2,u2)⋅P(x2∣x0:1,u0:2)⋅P(x0:1∣u0:2)=MarkovP(x3∣x2,u2)⋅P(x2∣x1,u1)P(x1∣x0,u0:2)⋅P(x0∣u0:2)=P(x3∣x2,u2)⋅P(x2∣x1,u1)⋅P(x1∣x0,u0)⋅P(x0)=Au2(x2,x3)⋅Au(x1,x2)⋅Au0(x0,x1)⋅η0x(x0) \begin{aligned} & P\left(x_{0: 3} \mid u_{0: 2}\right) \\ \overset{(\ast)}{=}& P\left(x_{3} \mid x_{0: 2}, u_{0: 2}\right) \cdot P\left(x_{0: 2} \mid u_{0: 2}\right) \\ \overset{\text{Markov}}{=}& P\left(x_{3} \mid x_{2}, u_{2}\right) \cdot P\left(x_{2} \mid x_{0: 1}, u_{0: 2}\right) \cdot P\left(x_{0: 1} \mid u_{0: 2}\right) \\ \overset{\text{Markov}}{=}& P\left(x_{3} \mid x_{2}, u_{2}\right) \cdot P\left(x_{2} \mid x_{1}, u_{1}\right) P\left(x_{1} \mid x_{0}, u_{0: 2}\right) \cdot P\left(x_{0} \mid u_{0: 2}\right) \\ =& P\left(x_{3} \mid x_{2}, u_{2}\right) \cdot P\left(x_{2} \mid x_{1}, u_{1}\right) \cdot P\left(x_{1} \mid x_{0}, u_{0}\right) \cdot P\left(x_{0}\right) \\ =& A_{u_{2}}\left(x_{2}, x_{3}\right) \cdot A_{u}\left(x_{1}, x_{2}\right) \cdot A_{u_{0}}\left(x_{0}, x_{1}\right) \cdot \eta_{0}^{x}\left(x_{0}\right) \end{aligned}

Verbundverteilung für k=1,2,3k = 1, 2, 3:

P(x1:3∣u0:2)=∑x0=12P(x0:3∣u0:2)=P(x3∣x2,u2)⏟=Au2(x2,x3)⋅P(x2∣x1,u1)⏟=Au1(x1,x2)⋅∑x0=12P(x1∣x0,u0)⋅P(x0)⏟=P(x1∣u0)=η1∗(x1) \begin{aligned} P\left(x_{1: 3} \mid u_{0: 2}\right) &=\sum_{x_{0}=1}^{2} P\left(x_{0: 3} \mid u_{0: 2}\right) \\ &=\underbrace{P\left(x_{3} \mid x_{2}, u_{2}\right)}_{=\mathbf{A}_{u_{2}}\left(x_{2}, x_{3}\right)} \cdot \underbrace{P\left(x_{2} \mid x_{1}, u_{1}\right)}_{=\mathbf{A}_{u_{1}}\left(x_{1}, x_{2}\right)} \cdot \underbrace{\sum_{x_0=1}^{2} P\left(x_{1} \mid x_{0}, u_{0}\right) \cdot P\left(x_{0}\right)}_{=P\left(x_{1} \mid u_{0}\right)=\eta_{1}^{*}\left(x_{1}\right)} \end{aligned}

P(x1:3∣u0:2)P\left(x_{1: 3} \mid u_{0: 2}\right) bedeutet: PP indiziert mit dem 3-dimensionalen Indexvekter (1,2,3)⊤(1, 2, 3)^\top. Jede von dem kann 2 Wer4te annehmen.

η1x(x1)=∑x0=12Au0(x0,x1)⋅η0x(x0)=Au0(x0=1,x1)P0⏟=P(x0=1)+Au0(x0=2,x1)(1−P0)⏟=P(x0=2)(Marginalisierung)={a1⋅pb+a2(1−p0)x1=1(1−a1)p0+(1−a2)(1−p0)x1=2 \begin{array}{l} \eta_{1}^{x}\left(x_{1}\right) &= \sum_{x_{0}=1}^{2} A_{u_{0}}\left(x_{0}, x_{1}\right) \cdot \eta_{0}^{x}\left(x_{0}\right)\\ &=A_{u_{0}}\left(x_{0}=1, x_{1}\right) \underbrace{{P}_{0}}_{=P(x_0 = 1)}+A_{u_{0}}\left(x_{0}=2, x_{1}\right) \underbrace{\left(1-P_{0}\right)}_{=P\left(x_{0}=2\right)} \quad (\text{Marginalisierung})\\ &=\left\{\begin{array}{ll} a_{1} \cdot p_{b}+a_{2}\left(1-p_{0}\right) & x_{1}=1 \\ \left(1-a_{1}\right) p_{0}+\left(1-a_{2}\right)\left(1-p_{0}\right) & x_{1}=2 \end{array}\right. \end{array} P(x3∣u0:2)=∑x2=12∑x1=12P(x1:3∣u0:2)=∑x2=12Au2(x2,x3)∑x1=12(x1,x2)η1x(x1)⏟=P(x1∣u0:1)=η2x(x1)=∑x2=12Au2(x2,x3)⋅η2x(x2)=η3x(x3) \begin{aligned} P\left(x_{3} \mid u_{0: 2}\right)=&\displaystyle \sum_{x_{2}=1}^{2} \sum_{x_{1}=1}^{2} P\left(x_{1: 3} \mid u_{0: 2}\right)\\ =&\displaystyle \sum_{x_{2}=1}^{2} A_{u_{2}}\left(x_{2}, x_{3}\right) \underbrace{\displaystyle \sum_{x_{1} = 1}^{2}\left(x_{1}, x_{2}\right) \eta_{1}^{x}\left(x_{1}\right)}_{=P\left(x_{1} \mid u_{0:1}\right)=\eta_{2}^{x}\left(x_{1}\right)}\\ =&\sum_{x_{2}=1}^{2} A_{u_{2}}\left(x_{2}, x_{3}\right) \cdot \eta_{2}^{x}\left(x_{2}\right)\\\\ =& \eta_{3}^{x}\left(x_{3}\right) \end{aligned} η3x=Au2⊤⋅η2x⏟=Au1⊤⋅η1x=Au2⊤⋅(Au1⊤⋅η1x⏟=Au0⊤⋅η0x)=Au2⊤⋅(Au1⊤⋅(Au0⊤⋅η0x)) (rekursive Berechnung)  \begin{aligned} \eta_{3}^{x} &=\mathbf{A}_{u_{2}}^{\top} \cdot \underbrace{\eta_{2}^{x}}_{=\mathbf{A}_{u_{1}}^{\top} \cdot \eta_{1}^{x}} \\ &=\mathbf{A}_{u_{2}}^{\top} \cdot (\mathbf{A}_{u_{1}}^{\top} \cdot \underbrace{\eta_{1}^{x}}_{=\mathbf{A}_{u_{0}}^{\top} \cdot \eta_{0}^{x}})\\ &=\mathbf{A}_{u_{2}}^{\top} \cdot (\mathbf{A}_{u_{1}}^{\top} \cdot (\mathbf{A}_{u_{0}}^{\top} \cdot \eta_{0}^{x})) \quad \text { (rekursive Berechnung) } \end{aligned}

Prädikition der Messungen für k=1,2,3k=1,2,3:

P(y1,y2,y3,x1:3∣u0:2)=(∗)P(y1:3∣x1:3,u0:2)⋅P(x1:3∣u0:2)=P(y1:3∣x1:3)P(x1:3∣u0:2)=P(y1∣x1:3)P(y2∣x1:3)P(y3∣x1:3)P(x1:3∣u0:2)=P(y1∣x1)⋅P(y2∣x2)⋅P(y3∣x3)P(x1:3∣u0:2)=B(x1,y1)B(x2,y2)B(x3,y3)P(x1:3∣u0:2) \begin{aligned} & P(y_{1}, y_{2}, y_{3}, x_{1: 3} \mid u_{0: 2}) \\\\ \overset{(\ast)}{=}& P\left(y_{1: 3} \mid x_{1: 3}, u_{0: 2}\right) \cdot P\left(x_{1: 3} \mid u_{0: 2}\right) \\\\ =& P\left(y_{1: 3} \mid x_{1: 3}\right) P\left(x_{1: 3} \mid u_{0: 2}\right) \\\\ =& P\left(y_{1} \mid x_{1: 3}\right) P\left(y_{2} \mid x_{1: 3}\right) P\left(y_{3} \mid x_{1: 3}\right) P\left(x_{1: 3} \mid u_{0: 2}\right) \\\\ =& P\left(y_{1} \mid x_{1}\right) \cdot P\left(y_{2} \mid x_{2}\right) \cdot P\left(y_{3} \mid x_{3}\right) P\left(x_{1: 3} \mid u_{0: 2}\right) \\\\ =& B\left(x_{1}, y_{1}\right) B\left(x_{2}, y_{2}\right) B\left(x_{3}, y_{3}\right) P\left(x_{1: 3} \mid u_{0: 2}\right) \end{aligned}

Prädikition Messung für k=3k=3:

P(y3,x3∣u0:2)=(∗)P(y3∣x3,u0:2)⋅P(x3∣u0:2)=P(y3∣x3)⋅P(x3∣u0:2)=B(x3,y3)⋅η3x(x3) \begin{aligned} & P\left(y_{3}, x_{3} \mid u_{0: 2}\right) \\ \overset{(\ast)}{=}& P\left(y_{3} \mid x_{3}, u_{0: 2}\right) \cdot P\left(x_{3} \mid u_{0: 2}\right) \\ =& P\left(y_{3} \mid x_{3}\right) \cdot P\left(x_{3} \mid u_{0: 2}\right) \\ =& B\left(x_{3}, y_{3}\right) \cdot \eta_{3}^{x}\left(x_{3}\right) \end{aligned}

Filterung (Wonham Filter)

Wie sieht P(xk∣y1:k,u0:k−1)P\left(x_{k} \mid y_{1: k}, u_{0: k-1}\right) auf Basis der Prädiktion P(xk∣y1:k−1,u0:k−1)P\left(x_{k} \mid y_{1: k-1}, u_{0: k-1}\right) aus?

wertdiskrete_systeme-Filterung.drawio

Reminder

P(b∣a,c)⋅P(a∣c)=P(a∣b,c)⋅P(b∣c)(△) P(b \mid a, c) \cdot P(a \mid c)=P(a \mid b, c) \cdot P(b \mid c) \quad (\triangle)
P(xk∣y1:k,u0:k−1)=P(xk⏟b∣yk⏟a,y1:k−1,u0:k−1)⏟c=(△)P(yk∣xk,y1:k−1,u0:k−1)⋅P(xk∣y1:k−1,u0:k−1)P(yk∣y1:k−1,u0:k−1)=P(yk∣xk)⏞Likelihood⋅P(xk∣y1:k−1,u0:k−1)⏞Einschritt-Pra¨diktionP(yk∣y1:k−1,u0:k−1)⏟Normalisierungskonstant \begin{aligned} & P\left(x_{k} \mid y_{1: k}, u_{0: k-1}\right) \\ =&\quad P(\underbrace{x_{k}}_{b} \mid \underbrace{y_{k}}_{a}, \underbrace{\left.y_{1: k-1}, u_{0: k-1}\right)}_{c}\\\\ \overset{(\triangle)}{=}& \frac{P\left(y_{k} \mid x_{k}, y_{1: k-1}, u_{0: k-1}\right) \cdot P\left(x_{k} \mid y_{1: k-1}, u_{0: k-1}\right)}{P\left(y_{k} \mid y_{1: k-1}, u_{0: k-1}\right)}\\\\ = & \frac{\overbrace{P\left(y_{k} \mid x_{k}\right)}^{\text{Likelihood}} \cdot \overbrace{P\left(x_{k} \mid y_{1: k-1}, u_{0: k-1}\right)}^{\text{Einschritt-Prädiktion}}}{\underbrace{P\left(y_{k} \mid y_{1: k-1}, u_{0: k-1}\right)}_{\text{Normalisierungskonstant}}} \end{aligned}
  • Likelihood
P(yk∣xk)=Bk(xk,yk)(Element aus Messmatrix) P\left(y_{k} \mid x_{k}\right)=B_{k}\left(x_{k}, y_{k}\right) \qquad(\text{Element aus Messmatrix})
  • Normalisierungskonstant
P(yk∣y1:k−1,u0:k−1)= Margin. ∑xk=1NP(yk,xk∣y1:k−1,u0:k−1)=(∗)∑xk=1NP(yk∣xk,y1:k−1,u0:k−1)⋅P(xk∣y1:k−1,u0:k−1)=∑xk=1NP(yk∣xk)⋅P(xk∣y1:k−1,u0:k−1) \begin{aligned} & P\left(y_{k} \mid y_{1: k-1}, u_{0: k-1}\right) \\\\ \stackrel{\text { Margin. }}{=} & \sum_{x_{k}=1}^{N} P\left(y_{k}, x_{k} \mid y_{1: k-1}, u_{0: k-1}\right) \\\\ \overset{(\ast)}{=}& \sum_{x_{k}=1}^{N} P\left(y_{k} \mid x_{k}, y_{1: k-1}, u_{0: k-1}\right) \cdot P\left(x_{k} \mid y_{1: k-1}, u_{0: k-1}\right) \\\\ =& \sum_{x_{k} = 1}^{N} P\left(y_{k} \mid x_{k}\right) \cdot P\left(x_{k} \mid y_{1: k-1}, u_{0: k-1}\right) \end{aligned}
  • Einschrittsprädikation
ηk∣1:k−1x=Ak⊤ηk−1∣1:k−1x \eta_{k \mid 1: k-1}^{x}=\mathbf{A}_{k}^{\top} \eta_{k-1\mid1: k-1}^{x}

Filterung in Vektor-Matrix-Form:

  • Für yk=my_k = m, Bilde eine Diagonalematrix diag⁡(B(:,m))\operatorname{diag}(\mathbf{B}(:, m)) mit Spalte des Messmatrix B(:,m)\mathbf{B}(:, m)

    ηk∣1:kx=yk=mdiag⁡(B(:,m))⋅ηk∣1:k−1x1NTdiag⁡(B(:,m))⋅ηk∣1:k−1x=B(:,m)⊙ηk∣1:k−1xB(:,m)⊤⋅ηk∣1:k−1x \begin{aligned} \eta_{k \mid 1: k}^{x} &\overset{y_k = m}{=}\frac{\operatorname{diag}(\mathbf{B}(:, m)) \cdot \eta_{k \mid 1: k-1}^{x}}{\mathbb{1}_{N}^{T} \operatorname{diag}(\mathbf{B}(:, m)) \cdot \eta_{k \mid 1: k-1}^{x}} \\\\ &=\frac{\mathbf{B}(:, m) \odot \eta_{k \mid 1: k-1}^{x}}{\mathbf{B}(:, m)^\top \cdot \eta_{k \mid 1:k-1}^{x}} \end{aligned}
    • 1N\mathbf{1}_N: Einsvektor
    • ⊙\odot: Elementwise-Multiplikation

Das ist ein komplett rekursives Filter →\rightarrow Wonham Filter

Beispiel siehe hier.