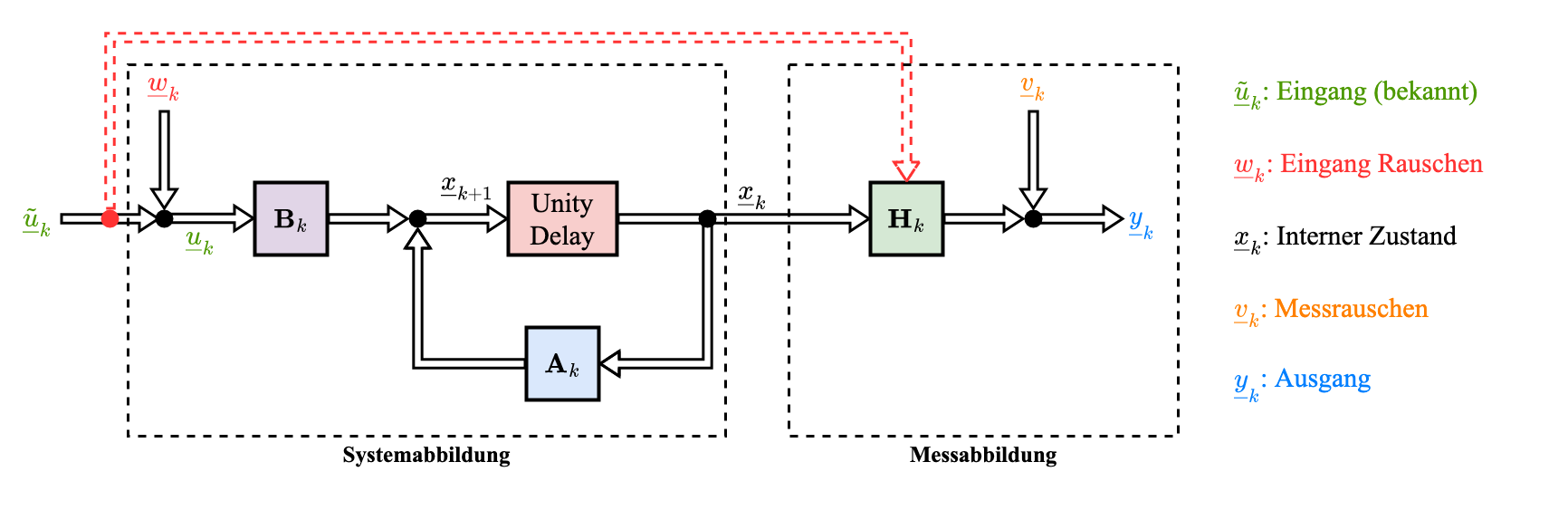
Zustandsschätzung: Kalman Filter Die ausführliche Zusammenfassung für Kalman Filter siehe hier . Prädiktion Wir möchte ein Schritt Prädiktion für Zustand machen, also am Zeitschritt k k k k > m k > m k > m m : = #Messungen m:= \text{\#Messungen} m := #Messungen x ‾ k + 1 \underline{x}_{k+1} x k + 1
Modell:
x ‾ k + 1 = A k ⋅ x ‾ k + B k ⋅ ( u ~ ‾ k + w ‾ k ) ⏟ u k ‾
\underline{x}_{k+1}=\mathbf{A}_{k} \cdot \underline{x}_{k}+\mathbf{B}_{k} \cdot \underbrace{\left(\underline{\tilde{u}}_{k}+\underline{w}_{k}\right)}_{\underline{u_k}}
x k + 1 = A k ⋅ x k + B k ⋅ u k ( u ~ k + w k ) Initialer Schätzwert für k k k
x ‾ k ∣ 1 : m
\underline{x}_{k|1:m}
x k ∣1 : m basiert auf Messungen y ‾ 1 , … , y ‾ m \underline{y}_{1}, \dots, \underline{y}_{m} y 1 , … , y m Eingabewerte u ~ ‾ 0 , … , u ~ ‾ k − 1 \underline{\tilde{u}}_{0}, \dots, \underline{\tilde{u}}_{k-1} u ~ 0 , … , u ~ k − 1 mit Erwartungswert x ^ ‾ k ∣ 1 : m \underline{\hat{x}}_{k|1:m} x ^ k ∣1 : m C k ∣ 1 : m x C_{k|1:m}^x C k ∣1 : m x Berechnung des Erwartungswerts für k + 1 k+1 k + 1
E { x ‾ k + 1 } = E { A k ⋅ x ‾ k + B k ( u ~ ‾ k + w ‾ k ) } = E { A k ⋅ x k + B k u ~ k + B k w ‾ k } = A k ⋅ E { x k } + B k ⋅ E { u ~ k } ⏟ = u ‾ ~ k (da u ‾ ~ k is fix) + B k ⋅ E { w ‾ k } ⏟ = 0 ("mittelwertfrei") = A k ⋅ x ^ ‾ k ∣ 1 : m + B k u ‾ ~ k ( + )
\begin{aligned}
&E\left\{\underline{x}_{k+1}\right\}\\\\
=&E\left\{\mathbf{A}_{k} \cdot \underline{x}_{k}+\mathbf{B}_{k}\left(\underline{\tilde{u}}_{k}+\underline{w}_{k}\right)\right\}\\\\
=&E\left\{\mathbf{A}_{k} \cdot x_{k}+\mathbf{B}_{k} \tilde{u}_{k}+\mathbf{B}_{k} \underline{w}_{k}\right\}\\\\
=&\mathbf{A}_{k} \cdot E\left\{x_{k}\right\}+\mathbf{B}_{k} \cdot \underbrace{E\left\{\tilde{u}_{k}\right\}}_{=\tilde{\underline{u}}_{k} \text{ (da } \tilde{\underline{u}}_{k} \text{ is fix)}}+\mathbf{B}_{k} \cdot\underbrace{E\left\{\underline{w}_{k}\right\}}_{=0 \text{ ("mittelwertfrei")}}\\\\
=&\mathbf{A}_{k} \cdot \underline{\hat{x}}_{k|1: m}+\mathbf{B}_{k} \tilde{\underline{u}}_{k} \qquad (+)
\end{aligned}
= = = = E { x k + 1 } E { A k ⋅ x k + B k ( u ~ k + w k ) } E { A k ⋅ x k + B k u ~ k + B k w k } A k ⋅ E { x k } + B k ⋅ = u ~ k (da u ~ k is fix) E { u ~ k } + B k ⋅ = 0 ("mittelwertfrei") E { w k } A k ⋅ x ^ k ∣1 : m + B k u ~ k ( + ) Berechnung der Kovarianzmatrix C k + 1 ∣ 1 : m x C_{k+1|1:m}^x C k + 1∣1 : m x
x ‾ k + 1 = A k x ‾ k + B k u ‾ k = [ A k B k ] [ x ‾ k u ‾ k ]
\begin{aligned}
\underline{x}_{k+1} &=\mathbf{A}_{k} \underline{x}_{k}+\mathbf{B}_{k} \underline{u}_{k} \\
&=\left[\begin{array}{ll}
\mathbf{A}_{k} & \mathbf{B}_{k}
\end{array}\right]\left[\begin{array}{c}
\underline{x}_{k} \\
\underline{u}_{k}
\end{array}\right]
\end{aligned}
x k + 1 = A k x k + B k u k = [ A k B k ] [ x k u k ] x ‾ k + 1 − x ‾ ^ k + 1 = [ A k B k ] [ x ‾ k − x ‾ ^ k u ‾ k − u ^ ‾ k ] = [ A k B k ] [ x ‾ k − x ^ ‾ k w ‾ k ]
\begin{aligned}
\underline{x}_{k+1}-\hat{\underline{x}}_{k+1} &=\left[\begin{array}{ll}
\mathbf{A}_{k} & \mathbf{B}_{k}
\end{array}\right]\left[\begin{array}{c}
\underline{x}_{k}-\hat{\underline{x}}_{k} \\
\underline{u}_{k}-\underline{\hat{u}}_{k}
\end{array}\right] \\
&=\left[\begin{array}{ll}
\mathbf{A}_{k} & \mathbf{B}_{k}
\end{array}\right]\left[\begin{array}{c}
\underline{x}_{k}-\underline{\hat{x}}_{k} \\
\underline{w}_{k}
\end{array}\right]
\end{aligned}
x k + 1 − x ^ k + 1 = [ A k B k ] [ x k − x ^ k u k − u ^ k ] = [ A k B k ] [ x k − x ^ k w k ] Annahme: Zustand und Systemrauschen sind unkorreliert
Cov { [ x ‾ k u ~ ‾ k ] } = E { [ x ‾ k − x ^ ‾ k w ‾ k ] [ ( x ‾ k − x ^ ‾ k ) ⊤ w ‾ k ⊤ ] } = [ C k ∣ 1 : m x 0 0 C k w ]
\begin{aligned}
\operatorname{Cov}\left\{\left[\begin{array}{c}
\underline{x}_{k} \\
\underline{\tilde{u}}_{k}
\end{array}\right]\right\} &=E\left\{\left[\begin{array}{c}
\underline{x}_{k}-\underline{\hat{x}}_{k} \\
\underline{w}_{k}
\end{array}\right]\left[\left(\underline{x}_{k}-\underline{\hat{x}}_{k}\right)^{\top} \underline{w}_{k}^{\top}\right]\right\} \\
&=\left[\begin{array}{cc}
C_{k \mid 1: m}^{x} & 0 \\
0 & C_{k}^{w}
\end{array}\right]
\end{aligned}
Cov { [ x k u ~ k ] } = E { [ x k − x ^ k w k ] [ ( x k − x ^ k ) ⊤ w k ⊤ ] } = [ C k ∣ 1 : m x 0 0 C k w ] C k + 1 ∣ 1 : m x = E { ( x ‾ k + 1 − x ^ k + 1 ) ( x k + 1 − x ‾ ^ k + 1 ) ⊤ } = [ A k B k ] ⋅ E { [ x ‾ k − x ‾ ^ k w ‾ k ] [ x ‾ k − x ‾ ^ k w ‾ k ] ⊤ } ⋅ [ A k ⊤ B k ⊤ ] = [ A k B k ] ⋅ [ C k ∣ 1 : m 0 0 C k w ] ⋅ [ A k ⊤ B k ⊤ ] = A k ⋅ C k ∣ 1 : m x A k ⊤ + B k C k w B k ⊤ ( + + )
\begin{aligned}
\mathbf{C}_{k+1 \mid 1 : m}^{x} &=E\left\{\left(\underline{x}_{k+1}-\hat{x}_{k+1}\right)\left(x_{k+1} - \hat{\underline{x}}_{k+1}\right)^\top\right\} \\
&=\left[\begin{array}{ll}
\mathbf{A}_{k} & \mathbf{B}_{k}
\end{array}\right] \cdot E\left\{\left[\begin{array}{c}
\underline{x}_{k}-\hat{\underline{x}}_{k} \\
\underline{w}_{k}
\end{array}\right]\left[\begin{array}{ll}
\underline{x}_{k}-\hat{\underline{x}}_{k} & \underline{w}_{k}
\end{array}\right]^\top\right\} \cdot\left[\begin{array}{l}
\mathbf{A}_{k}^{\top} \\
\mathbf{B}_{k}^{\top}
\end{array}\right] \\\\
&=\left[\begin{array}{ll}
\mathbf{A}_{k} & \mathbf{B}_{k}
\end{array}\right] \cdot\left[\begin{array}{cc}
\mathbf{C}_{k \mid 1:m} & 0 \\
0 & \mathbf{C}_{k}^{w}
\end{array}\right] \cdot\left[\begin{array}{l}
\mathbf{A}_{k}^{\top} \\
\mathbf{B}_{k}^{\top}
\end{array}\right] \\
&=\mathbf{A}_{k} \cdot \mathbf{C}_{k \mid 1: m}^{x} \mathbf{A}_{k}^{\top}+\mathbf{B}_{k} \mathbf{C}_{k}^{w} \mathbf{B}_{k}^{\top} \qquad(++)
\end{aligned}
C k + 1 ∣ 1 : m x = E { ( x k + 1 − x ^ k + 1 ) ( x k + 1 − x ^ k + 1 ) ⊤ } = [ A k B k ] ⋅ E { [ x k − x ^ k w k ] [ x k − x ^ k w k ] ⊤ } ⋅ [ A k ⊤ B k ⊤ ] = [ A k B k ] ⋅ [ C k ∣ 1 : m 0 0 C k w ] ⋅ [ A k ⊤ B k ⊤ ] = A k ⋅ C k ∣ 1 : m x A k ⊤ + B k C k w B k ⊤ ( + + ) Rekursive Prädiktion
Beispiele: Übungsblatt 5, Aufgabe 4 Filterung Ansatz: Linearer Schätzer
x ‾ k ∣ 1 : k = K k ( 1 ) x ‾ k ∣ 1 : k − 1 + K k ( 2 ) y ‾ k ( ∗ )
\underline{x}_{k \mid 1: k}=\mathbf{K}_{k}^{(1)} \underline{x}_{k \mid 1: k-1}+\mathbf{K}_{k}^{(2)} \underline{y}_{k} \qquad(\ast)
x k ∣ 1 : k = K k ( 1 ) x k ∣ 1 : k − 1 + K k ( 2 ) y k ( ∗ ) 🎯 Wir suchen den sog. BLUE-Filter (Best Linear Unbiased Estimator) 💪
Ein Schätzer heißt erwartungstreu
Ist eine Schätzfunktion nicht erwartungstreu, spricht man davon, dass der Schätzer verzerrt Verzerrung oder Bias . Die Verzerrung drückt den systematischen Fehler des Schätzers aus.
Source und Bsp: Wiki
Setze in ( ∗ ) (\ast) ( ∗ )
x ‾ k ∣ 1 : k ⏟ = : x ‾ k e = ( I − K k H k ) x ‾ k ∣ 1 : k − 1 ⏟ = : x ‾ k p + K k y ‾ k ( ∗ ∗ )
\underbrace{\underline{x}_{k \mid 1: k}}_{=: \underline{x}_{k}^{e}}=\left(\mathbf{I}-\mathbf{K}_{k}\mathbf{H}_{k} \right) \underbrace{\underline{x}_{k \mid 1: k-1}}_{=: \underline{x}_{k}^{p}}+\mathbf{K}_{k} \underline{y}_{k} \qquad(* *)
=: x k e x k ∣ 1 : k = ( I − K k H k ) =: x k p x k ∣ 1 : k − 1 + K k y k ( ∗ ∗ ) Aber der Schätzert ist noch nicht vollständig festgelegt, da K k \mathbf{K}_{k} K k
⇒ \Rightarrow ⇒ K k \mathbf{K}_{k} K k
Nehme an, dass Messung unkorreliert mit priorer Schätzung. Aus ( ∗ ∗ ) (\ast\ast) ( ∗ ∗ )
C k ∣ 1 : k ( K k ) ⏟ = : C k e ( K k ) = ( I − K k H k ) C k ∣ 1 : k − 1 x ⏟ = : C k p ( I − K k H k ) ⊤ + K k C k v K k ⊤ ( ∗ ∗ ∗ )
\underbrace{\mathbf{C}_{k \mid 1: k}\left(\mathbf{K}_{k}\right)}_{=: \mathbf{C}_{k}^{e}\left(\mathbf{K}_{k}\right)}=\left(\mathbf{I}-\mathbf{K}_{k} \mathbf{H}_{k}\right) \underbrace{\mathbf{C}_{k \mid 1: k-1}^{x}}_{=: \mathbf{C}_{k}^{p}}\left(\mathbf{I}-\mathbf{K}_{k} \mathbf{H}_{k}\right)^{\top}+\mathbf{K}_{k} C_{k}^{v} \mathbf{K}_{k}^{\top} \qquad(\ast\ast\ast)
=: C k e ( K k ) C k ∣ 1 : k ( K k ) = ( I − K k H k ) =: C k p C k ∣ 1 : k − 1 x ( I − K k H k ) ⊤ + K k C k v K k ⊤ ( ∗ ∗ ∗ ) Wir betrachten nun die Filterkovarianz C k e \mathbf{C}_{k}^{e} C k e K k \mathbf{K}_{k} K k C k e ( K k ) \mathbf{C}_{k}^{e}(\mathbf{K}_k) C k e ( K k ) K k \mathbf{K}_{k} K k
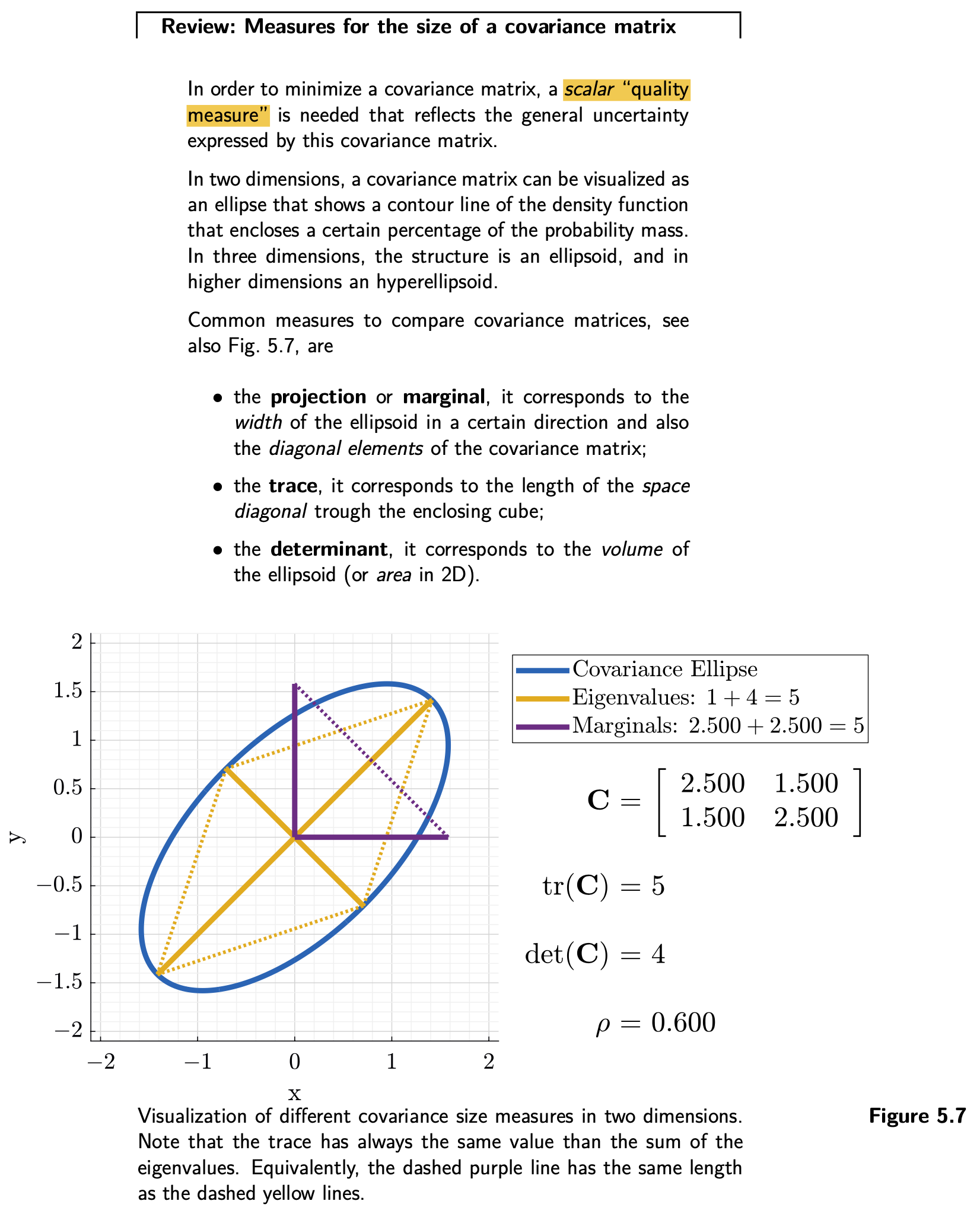
Trick: Auf Skalares Gütemaß zurückzuführen
D.h., um Kovarianzmatrizen generell vergleichen zu können, verwende man die Funktionen, die von einer n × n n \times n n × n R 1 \mathbb{R}^1 R 1
Z.B., Projektion mit beliebigen Einheitsvektor e ‾ \underline{e} e
P ( K ) = e ‾ ⊤ ⋅ C c ( K ) ⋅ e ‾
P(\mathbf{K}) = \underline{e}^\top \cdot \mathbf{C}_c(\mathbf{K}) \cdot \underline{e}
P ( K ) = e ⊤ ⋅ C c ( K ) ⋅ e MINIMAL Kovarianz ⇔ \Leftrightarrow ⇔ P ( K ) P(\mathbf{K}) P ( K ) e ‾ \underline{e} e
Andere mögliche skalare Gütemaße:
Spur ( ⋅ ) \operatorname{Spur}(\cdot) Spur ( ⋅ )
Spur ( C ) = σ _ x 2 + σ _ y 2
\begin{equation}
\operatorname{Spur}(\mathbf{C})=\sigma\_{x}^{2}+\sigma\_{y}^{2}
\end{equation}
Spur ( C ) = σ _ x 2 + σ _ y 2 det ( ⋅ ) \operatorname{det}(\cdot) det ( ⋅ )
det ( C ) = σ _ x 2 ⋅ σ _ y 2
\operatorname{det}(\mathbf{C})=\sigma\_{x}^{2} \cdot \sigma\_{y}^{2}
det ( C ) = σ _ x 2 ⋅ σ _ y 2 Beispiel Ableitung mit der Matrizen Differenzregeln :
∂ ∂ K P ( K ) = ∂ ∂ K { e ‾ ⊤ [ ( I − K H ) C p ( I − K H ) ⊤ + K C y K ⊤ ] e ‾ } = ∂ ∂ K { e ‾ ⊤ [ C p − C p H ⊤ K ⊤ − K H C p + K H C p H ⊤ K ⊤ + K C y K ⊤ ] e ‾ } = − [ H C p e ‾ e ‾ ⊤ ] ⊤ − e ‾ e ‾ ⊤ ( H C p ) ⊤ + 2 e ‾ e ‾ ⊤ K H C p H ⊤ + 2 e ‾ e ‾ ⊤ ⋅ K C y = ! 0
\begin{aligned}
\frac{\partial}{\partial \mathbf{K}} P(\mathbf{K}) &=\frac{\partial}{\partial \mathbf{K}}\left\{\underline{e}^{\top}\left[(\mathbf{I}-\mathbf{K} \mathbf{H}) \mathbf{C}_{p}(\mathbf{I}-\mathbf{K} \mathbf{H})^{\top}+\mathbf{K} \mathbf{C}_{y} \mathbf{K}^{\top}\right] \underline{e}\right\} \\
&=\frac{\partial}{\partial \mathbf{K}}\left\{\underline{e}^{\top}\left[\mathbf{C}_{p}-\mathbf{C}_{p} \mathbf{H}^{\top} \mathbf{K}^{\top}-\mathbf{K} \mathbf{H} \mathbf{C}_{p}+\mathbf{K} \mathbf{H} \mathbf{C}_{p} \mathbf{H}^{\top} \mathbf{K}^{\top}+\mathbf{K} \mathbf{C}_{y} \mathbf{K}^{\top}\right] \underline{e}\right\} \\
&=-\left[\mathbf{H} \mathbf{C}_{p} \underline{e} \underline{e}^{\top}\right]^{\top}-\underline{e} \underline{e}^{\top}\left(\mathbf{H} \mathbf{C}_{p}\right)^{\top}+2 \underline{e} \underline{e}^{\top} \mathbf{K} \mathbf{H} \mathbf{C}_{p} \mathbf{H}^{\top}+2 \underline{e} \underline{e}^{\top} \cdot \mathbf{K} \mathbf{C}_{y} \\
&\overset{!}{=} \mathbf{0}
\end{aligned}
∂ K ∂ P ( K ) = ∂ K ∂ { e ⊤ [ ( I − KH ) C p ( I − KH ) ⊤ + K C y K ⊤ ] e } = ∂ K ∂ { e ⊤ [ C p − C p H ⊤ K ⊤ − KH C p + KH C p H ⊤ K ⊤ + K C y K ⊤ ] e } = − [ H C p e e ⊤ ] ⊤ − e e ⊤ ( H C p ) ⊤ + 2 e e ⊤ KH C p H ⊤ + 2 e e ⊤ ⋅ K C y = ! 0 Also
− C p ⋅ H ⊤ − C p H ⊤ + 2 K H C p H ⊤ + 2 K C y = ! 0 K ( C y + H C p H ) ⊤ = C p H ⊤ K = C p H ⊤ ( C y + H C p H ⊤ ) − 1 (Kalman gain)
\begin{array}{l}
-\mathbf{C}_{p} \cdot \mathbf{\mathbf{H}}^{\top}-\mathbf{C}_{p} \mathbf{H}^{\top}+2 \mathbf{K} \mathbf{H} \mathbf{C}_{p} \mathbf{H}^{\top}+2 \mathbf{K} \mathbf{C}_{y} \stackrel{!}{=} \mathbf{0} \\
\mathbf{K}\left(\mathbf{C}_{y}+\mathbf{H} \mathbf{C}_{p} \mathbf{H}\right)^{\top}=\mathbf{C}_{p} \mathbf{H}^{\top} \\
\mathbf{K}=\mathbf{C}_{p} \mathbf{H}^{\top}\left(\mathbf{C}_{y}+\mathbf{H} \mathbf{C}_{p} \mathbf{\mathbf{H}}^{\top}\right)^{-1} \quad \text { (Kalman gain) }
\end{array}
− C p ⋅ H ⊤ − C p H ⊤ + 2 KH C p H ⊤ + 2 K C y = ! 0 K ( C y + H C p H ) ⊤ = C p H ⊤ K = C p H ⊤ ( C y + H C p H ⊤ ) − 1 (Kalman gain) Setze K \mathbf{K} K ( ∗ ∗ ) (\ast \ast) ( ∗ ∗ )
x ^ ‾ e = ( I − K H ) x ^ ‾ p + K ⋅ y ^ ‾ (combination form) = x ^ ‾ p + K ( y ^ ‾ − H ⋅ x ^ ‾ p ) (feedback form) = x ^ ‾ p + C p H ⊤ ( C y + H C p H ⊤ ) − 1 ( y ‾ − H ⋅ x ^ ‾ p )
\begin{aligned}
\underline{\hat{x}}_{e} &=(\mathbf{I}-\mathbf{K} \mathbf{H}) \underline{\hat{x}}_{p}+\mathbf{K} \cdot \underline{\hat{y}} \qquad \text { (combination form) } \\
&=\underline{\hat{x}}_{p}+\mathbf{K}\left(\underline{\hat{y}}-\mathbf{H} \cdot \underline{\hat{x}}_{p}\right) \qquad \text { (feedback form) } \\
&=\underline{\hat{x}}_{p}+\mathbf{C}_{p} \mathbf{H}^{\top}\left(\mathbf{C}_{y}+\mathbf{H} \mathbf{C}_{p} \mathbf{H}^{\top}\right)^{-1}\left(\underline{y}-\mathbf{H} \cdot \underline{\hat{x}}_{p}\right)
\end{aligned}
x ^ e = ( I − KH ) x ^ p + K ⋅ y ^ (combination form) = x ^ p + K ( y ^ − H ⋅ x ^ p ) (feedback form) = x ^ p + C p H ⊤ ( C y + H C p H ⊤ ) − 1 ( y − H ⋅ x ^ p ) Das ist das Kalman Filter
Nun Setze K \mathbf{K} K ( ∗ ∗ ∗ ) (\ast \ast \ast) ( ∗ ∗ ∗ )
C e = [ I − C p H ⊤ ( C y + H C p H ⊤ ) − 1 H k ] ⋅ C p ⋅ [ I − C p H ⊤ ( C y + H C p H ⊤ ) − 1 H k ] − 1 + C p H ⊤ ( C y + H C p H ⊤ ) − 1 C y ( C y + H C p H ⊤ ) − 1 H C p = C p − 2 C p H ⊤ ( C y + H C p H ⊤ ) − 1 H C p + C p H ⊤ ( C y + H C p H ⊤ ) − 1 H C p H ⊤ ( C y + H C p H ⊤ ) − 1 H C p + C p H ⊤ ( C y + H C p H ⊤ ⏟ = : D ) − 1 C y ( C y + H C p H ⊤ ) − 1 H C p = C p − 2 C p H ⊤ D − 1 H C p + C p H ⊤ D − 1 D D − 1 H C p = C p − C p H ⊤ ( C y + H C p H ⊤ ) − 1 H C p
\begin{aligned}
\mathbf{C}_{e}=& {\left[\mathbf{I}-\mathbf{C}_{p} \mathbf{H}^{\top}\left(\mathbf{C}_{y}+\mathbf{H} \mathbf{C}_{p} \mathbf{H}^{\top}\right)^{-1} \mathbf{H}_{k}\right] \cdot \mathbf{C}_{p} } \\
& \cdot\left[\mathbf{I}-\mathbf{C}_{p} \mathbf{H}^{\top}\left(\mathbf{C}_{y}+\mathbf{H} \mathbf{C}_{p} \mathbf{H}^{\top}\right)^{-1} \mathbf{H}_{k}\right]^{-1} \\
&+\mathbf{C}_{p} \mathbf{H}^{\top}\left(\mathbf{C}_{y}+\mathbf{H} \mathbf{C}_{p} \mathbf{H}^{\top}\right)^{-1} \mathbf{C}_{y}\left(\mathbf{C}_{y}+\mathbf{H} \mathbf{C}_{p} \mathbf{H}^{\top}\right)^{-1} \mathbf{H} \mathbf{C}_{p} \\\\
=& \mathbf{C}_{p}-2 \mathbf{C}_{p} \mathbf{H}^{\top}\left(\mathbf{C}_{y}+\mathbf{H} \mathbf{C}_{p} \mathbf{H}^{\top}\right)^{-1} \mathbf{H} \mathbf{C}_{p} \\
&+\mathbf{C}_{p} \mathbf{H}^{\top}\left(\mathbf{C}_{y}+\mathbf{H} \mathbf{C}_{p} \mathbf{H}^{\top}\right)^{-1} \mathbf{H} \mathbf{C}_{p} \mathbf{H}^{\top}\left(\mathbf{C}_{y}+\mathbf{H} \mathbf{C}_{p} \mathbf{H}^{\top}\right)^{-1} \mathbf{H} \mathbf{C}_{p} \\
&+\mathbf{C}_{p} \mathbf{H}^{\top}(\underbrace{\mathbf{C}_{y}+\mathbf{H} \mathbf{C}_{p} \mathbf{H}^{\top}}_{=:\mathbf{D}})^{-1} \mathbf{C}_{y}\left(\mathbf{C}_{y}+\mathbf{H} \mathbf{C}_{p} \mathbf{H}^{\top}\right)^{-1} \mathbf{H} \mathbf{C}_{p}\\\\
=& \mathbf{C}_{p}-2 \mathbf{C}_{p} \mathbf{H}^{\top} \mathbf{D}^{-1} \mathbf{H} \mathbf{C}_{p}+\mathbf{C}_{p} \mathbf{H}^{\top} \mathbf{D}^{-1} \mathbf{D} \mathbf{D}^{-1} \mathbf{H} \mathbf{C}_{p} \\\\
=& \mathbf{C}_{p}-\mathbf{C}_{p} \mathbf{H}^{\top}\left(\mathbf{C}_{y}+\mathbf{H} \mathbf{C}_{p} \mathbf{H}^{\top}\right)^{-1} \mathbf{H} \mathbf{C}_{p}
\end{aligned}
C e = = = = [ I − C p H ⊤ ( C y + H C p H ⊤ ) − 1 H k ] ⋅ C p ⋅ [ I − C p H ⊤ ( C y + H C p H ⊤ ) − 1 H k ] − 1 + C p H ⊤ ( C y + H C p H ⊤ ) − 1 C y ( C y + H C p H ⊤ ) − 1 H C p C p − 2 C p H ⊤ ( C y + H C p H ⊤ ) − 1 H C p + C p H ⊤ ( C y + H C p H ⊤ ) − 1 H C p H ⊤ ( C y + H C p H ⊤ ) − 1 H C p + C p H ⊤ ( =: D C y + H C p H ⊤ ) − 1 C y ( C y + H C p H ⊤ ) − 1 H C p C p − 2 C p H ⊤ D − 1 H C p + C p H ⊤ D − 1 D D − 1 H C p C p − C p H ⊤ ( C y + H C p H ⊤ ) − 1 H C p Schritt für Schritt Herleitung: Übungsblatt 6, Aufgabe 1 (Sehr ausführlich und hilfreich! 👍) Beispiel Kompletter Kalman Filter: Übungsblatt 5 Aufgabe 3
Prädiktion: Übungsblatt 5, Aufgabe 4
Filterung: Übungsblatt 6 Aufgabe 1